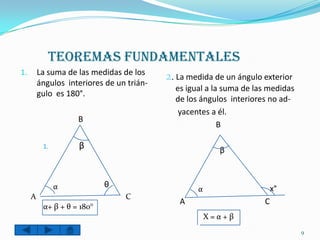
Este documento trata sobre triángulos. Define un triángulo y sus elementos básicos como lados y vértices. Clasifica los triángulos según sus lados en equilátero, isósceles y escaleno, y según sus ángulos en agudos, rectos y obtusos. Presenta cuatro teoremas fundamentales sobre triángulos. Finalmente, incluye dos ejemplos resueltos de problemas geométricos sobre triángulos.

1. Triángulos
1

2.  Definición
 Elementos
 Clasificación
 Teoremas Fundamentales
 Ejercicios
2

3. definición
Se define como la porción de plano delimitado por tres rectas que se cortan dos
a dos , o como la porción común de tres semiplanos pertenecientes a un mismo
semiplano.
α
β
λ
3

4. elementos
B
Y Lados: AB, BC, CA
α
Vértices: A, B, C
Ángulos internos:
Z α, β, λ
A β λ Ángulos externos:
X C X, Y, Z
4

5. CLASIFICACIÓN
Los triángulos se clasifican de la siguiente manera:
 I. DE ACUERDO A SUS LADOS
 a) EQUILÁTERO: Tiene sus tres lados congruentes. Cada ángulo interior
mide 60° .
B
60º
60º 60º
A C
5

6. c) ESCALENO : Es el que tiene tres
b) ISÓSCELES: Si tiene dos lados
lados desiguales.
congruentes. El tercero es llamado
base.
Los ángulos en la base son B
congruentes.
B
A C
A BASE C
6

7. b) OBLICUÁNGULOS : Cuando no tiene un ángulo interior recto (90° ).
Pueden ser :
OBTUSÁNGULO : Si uno de sus
ACUTÁNGULO: Si sus tres ángulos
ángulos interiores es obtuso.
interiores son agudos.
B
B
θ θ
µ
α α β
C A
A C
β >90°
α° ; θ° ; µ° < 90°
7

8. II. DE ACUERDO A SUS ÁNGULOS
a) RECTÁNGULO: Si uno de sus ángulos mide 90° ( ángulo recto)
Los lados que forman dicho ángulo se llaman catetos y el opuesto a estos
se llama hipotenusa.
La Longitud de la hipotenusa es mayor que la de los catetos.
B
C α
A HIPOTENUSA
c T a
E a > b
T
O 90°- α a > c
A CATETO C
b
8

9. TEOREMAS FUNDAMENTALES
1. La suma de las medidas de los
2. La medida de un ángulo exterior
ángulos interiores de un trián-
es igual a la suma de las medidas
gulo es 180°.
de los ángulos interiores no ad-
yacentes a él.
B
B
1. β β
α θ α x°
A C
A C
α+ β + θ = 180°
X=α+β
9

10. 3. La suma de las medidas de los 4. En todo triángulo, la longitud de
ángulos exteriores , uno por vér- uno de sus lados es menor que la
tice es igual a 360° . suma de las longitudes de los
otros dos, pero a su vez mayor
que su diferencia.
B
y Si: c<b<a b<a + c
b>a–c
x z
A C a–c<b<a+c
x+ y + z = 360°
10

11. Ejercicios Resueltos
1.- En la figura : Hallar “x” B  2.- En la figura: Hallar m < BAC
20º
100º
B
x α
A C 98º
2x
Solución 40º X + 30º
A
ABD, isósceles : AB = BD C
D
DBC, isósceles: BC = BD Resolución:
Del gráfico vemos que m< BAC= x = ?
Luego: ABC, Isósceles ya que AB = BC
Por el teorema del ángulo exterior
α = 30º y x = 20º + α m < externo = m < A + m < B
2x + x + 30 = x + 98
x = 50º
2x = 68º
x = 34º
11