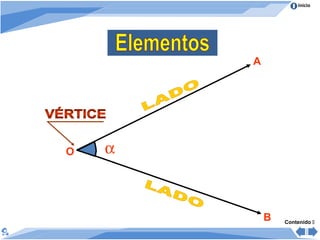
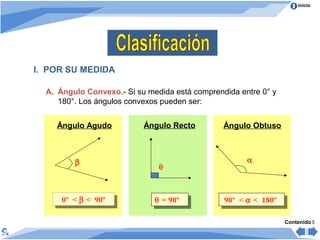
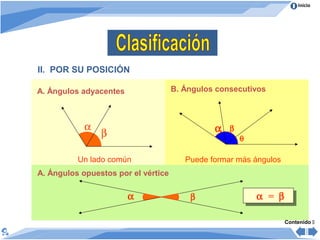
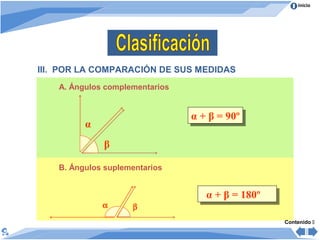
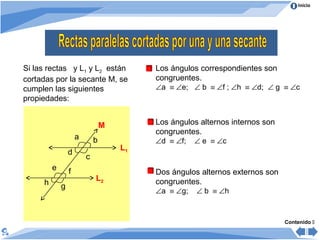
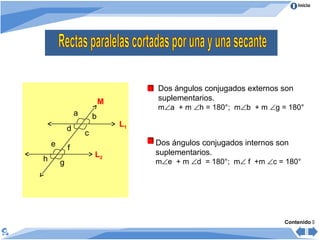
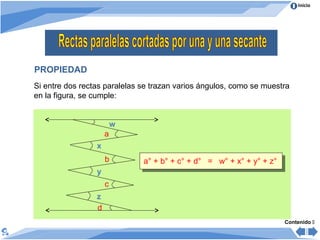
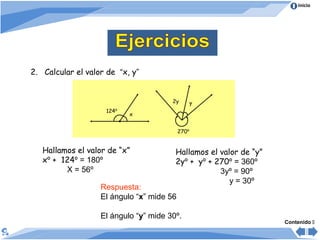
El documento trata sobre los ángulos. Explica que un ángulo se forma por dos rayos que parten de un punto común llamado vértice. Luego clasifica los ángulos de acuerdo a su medida en agudos, rectos, obtusos, llano y no convexos. También los clasifica según su posición en adyacentes, consecutivos y opuestos. Finalmente, presenta propiedades de ángulos formados cuando dos rectas son cortadas por una secante.

1. ÁNGULOSÁNGULOS
RecursosRecursos
Contenido TemáticoContenido Temático
PresentaciónPresentación
EvaluaciónEvaluación

2. Inicio
En este tema se comprenderá el concepto de ángulos,
reconoceremos los elementos y clasificaremos los ángulos según
diversos criterios.
Presentación
La geometría es una parte importante de
la cultura del hombre, no es fácil encontrar
contextos en que la geometría no aparezca
de forma directa o indirecta. Actividades
tan variadas como el deporte, la jardinería
o la arquitectura por citar algunas se sirven
de la utilización, consciente o no, de
procedimientos geométricos.

3. Inicio
Contenido Temático
Definición
Elementos
Clasificación
Rectas paralelas cortadas por una secante

4. Inicio
Ángulo es la abertura formada por dos rayos (lados) que parten
de un punto común llamado vértice.
Contenido 

5. Inicio
O
A
B
α
Contenido 

6. Inicio
I. POR SU MEDIDA
A. Ángulo Convexo.- Si su medida está comprendida entre 0° y
180°. Los ángulos convexos pueden ser:
Ángulo Agudo
0º < β < 90º0º < β < 90º
β
Ángulo Recto Ángulo Obtuso
θ = 90ºθ = 90º 90º < α < 180º90º < α < 180º
α
θ
Contenido 

7. Inicio
I. POR SU MEDIDA
B. Ángulo Llano.- Su medida es 180°. Sus lados son 2 rayos
opuestos
θ = 180ºθ = 180º
θ
Contenido 

8. Inicio
I. POR SU MEDIDA
C. Ángulo no convexo.- Si su medida está comprendida entre 180° y
360°.
D. Ángulo de una vuelta (Perigonal).- Si su medida es 360°.
Teorema: La suma de las medidas de los ángulos consecutivos,
formados alrededor de un mismo vértice y en un mismo plano es
360°.
θ
β
α
α + β + θ = 360°α + β + θ = 360°
Contenido 

9. Inicio
II. POR SU POSICIÓN
α
β
A. Ángulos adyacentes
Un lado común
α β
θ
B. Ángulos consecutivos
Puede formar más ángulos
A. Ángulos opuestos por el vértice
α β α = βα = β
Contenido 

10. Inicio
III. POR LA COMPARACIÓN DE SUS MEDIDAS
α + β = 90ºα + β = 90º
α
β
A. Ángulos complementarios
α + β = 180ºα + β = 180º
βα
B. Ángulos suplementarios
Contenido 

11. Inicio
Si las rectas y L1 y L2 están
cortadas por la secante M, se
cumplen las siguientes
propiedades:
Los ángulos correspondientes son
congruentes.
∠a ≡ ∠e; ∠ b ≡ ∠f ; ∠h ≡ ∠d; ∠ g ≡ ∠c
a b
h g
fe
d
c
L1
L2
M
Contenido 
Los ángulos alternos internos son
congruentes.
∠d ≡ ∠f; ∠ e ≡ ∠c
Dos ángulos alternos externos son
congruentes.
∠a ≡ ∠g; ∠ b ≡ ∠h

12. Inicio
Dos ángulos conjugados externos son
suplementarios.
m∠a + m ∠h = 180°; m∠b + m ∠g = 180°
a b
h g
fe
d
c
L1
L2
M
Contenido 
Dos ángulos conjugados internos son
suplementarios.
m∠e + m ∠d = 180°; m∠ f +m ∠c = 180°

13. Inicio
PROPIEDAD
Si entre dos rectas paralelas se trazan varios ángulos, como se muestra
en la figura, se cumple:
w
x
y
z
a
b
c
d
a° + b° + c° + d° = w° + x° + y° + z°
Contenido 

14. Inicio
Resolución
1. Los ángulos mostrados son congruentes. Hallar el valor de “x”.
xº + 15º = 45º
X = 30º
Respuesta:
El ángulo “x” mide 30º
Contenido 
xº + 15º
45º

15. Inicio
2. Calcular el valor de “x, y”
Resolución
Hallamos el valor de “x”
xº + 124º = 180º
X = 56º
Respuesta:
El ángulo “x” mide 56
El ángulo “y” mide 30º.
Contenido 
124º
x
270º
y2y
Hallamos el valor de “y”
2yº + yº + 270º = 360º
3yº = 90º
y = 30º