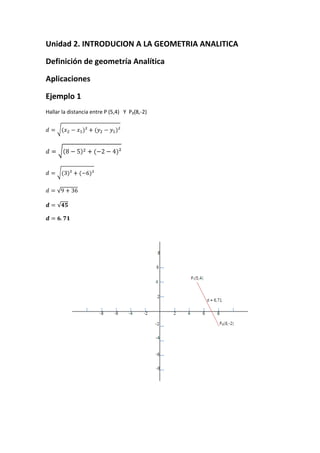
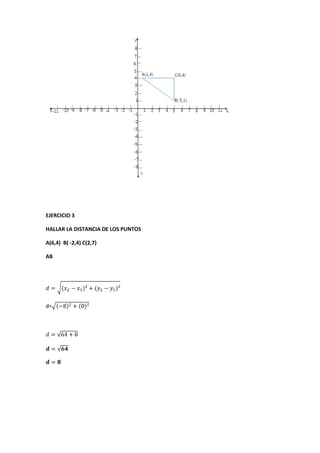
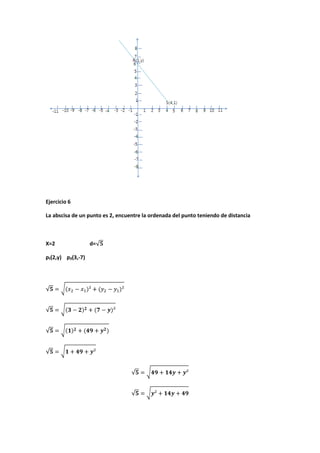
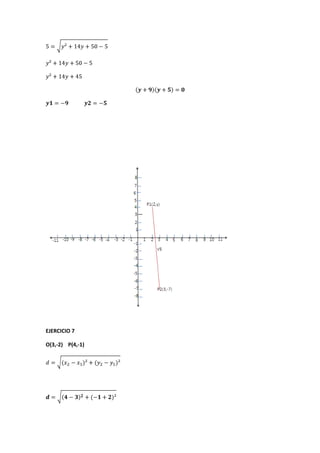
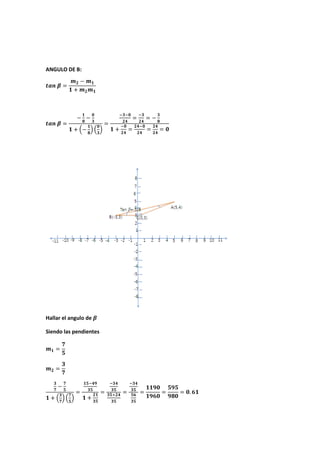
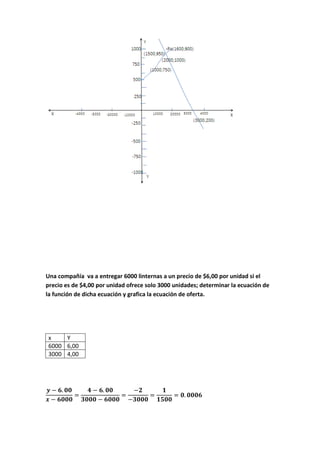
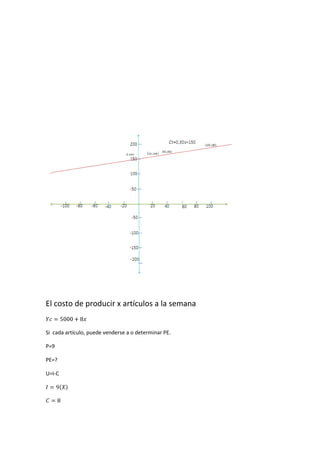
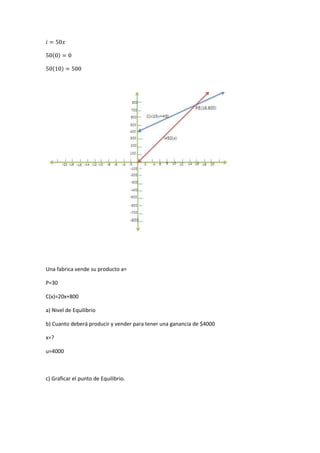
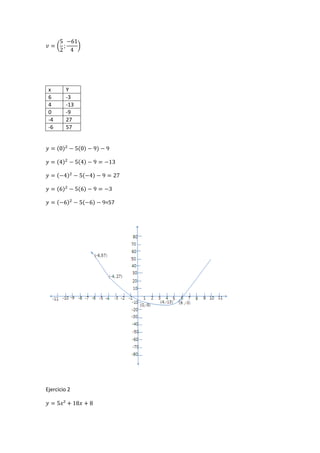
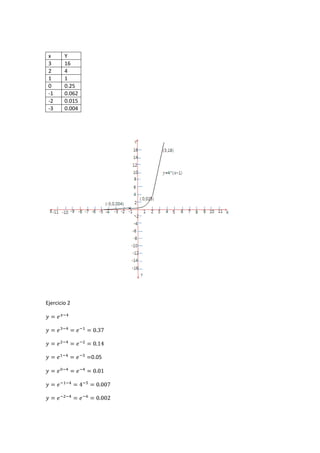
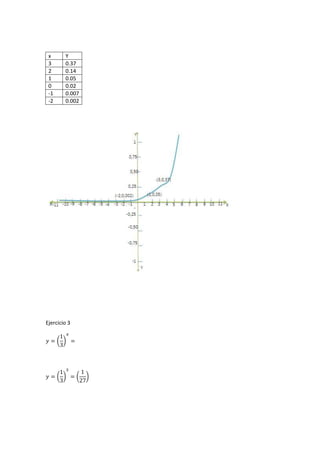
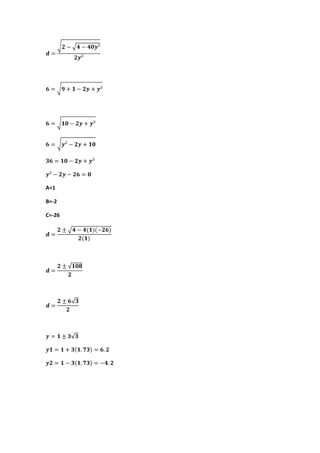Este documento introduce la geometría analítica y presenta ejemplos de cálculo de distancias entre puntos, perímetros de triángulos dados sus vértices, ecuaciones de rectas y puntos medios. También cubre temas como pendientes, ángulos entre rectas, ecuaciones de rectas dadas un punto y pendiente, y aplicaciones de funciones lineales como oferta y demanda.

1. Unidad 2. INTRODUCION A LA GEOMETRIA ANALITICA
Definición de geometría Analítica
Aplicaciones
Ejemplo 1
Hallar la distancia entre P (5,4) Y P₂(8,-2)

2. Ejemplo 2
Los vértices de un triangulo tienen las coordenadas dadas.
• Encontrar el perímetro
• Encontrar su distancia.
A(1,4) ; B(5,1) ; C(5,4)
AB
BC

3. CA
El perímetro
P= AB + BC +CA
P=5 + 3 + 4 =
P= 12

4. EJERCICIO 3
HALLAR LA DISTANCIA DE LOS PUNTOS
A(6,4) B( -2,4) C(2,7)
AB
d=

5. BC
CA
El perímetro
P= AB+BC+CA
P=8+5+5
P=18

6. HALLAR LA DISTANCIA DE LOS PUNTOS
A(1,0) B(3.4) C(-7,6)
AB
BC

7. CA

8. Ejercicio 5
Demuestre que la distancia entre los dos puntos es 6
R(1,y) s(4 ,1)

9. A=1
B=-2
C=-26

10. Ejercicio 6
La abscisa de un punto es 2, encuentre la ordenada del punto teniendo de distancia
X=2 d=
p₁(2,y) p₂(3,-7)

11. EJERCICIO 7
O(3,-2) P(4,-1)

12. EJERCICIO 8
HALLAR LA DISTANCIA DE LOS PUNTOS
T(5,-3) U=(-12-3)

13. |
PUNTO MEDIO DE UN SEGMENTO
EJRCICIO 1
A=(1,5)
B=(6,7)
C=(10,1)

14. BC
CA
HALLAR LOS PUNTOS MEDIOS DE:
X(-5,3) Y(-5-2)

15. LOS PUNTOS MEDIOS DE:
F(5,3) G(-12,3)
LOS PUNTOS MEDIOS DE:
J(1,2) K(-2,3)

16. HALLAR EL PUNTO MEDIO DE ESTOS PUNTOS
D(-3-2) E(5,3)
HALLAR EL PUNTO MEDIO DE :
L(0,3) M(1,5)

17. HALLA LOS PÚNTOS MEDIOS DE:
V(-2,-1) W(-3,4)
HALLAR LOS PUNTOS MEDIOS DE :
P(-4,6) Q( -7,6)
HALLAR LOS PUNTOS MEDIOS
R (2,4) S (3,4)

18. HALLAR LOS PUNTOS MEDIOS DE:
Y(7,8) Z(4,5)
INCLINACION Y PENDIENTE
HALLAR LA PENDIENTE DE:
S(5,2) R( -3,-1)
HALLAR LA PENDIENTE DE:
C(-3,4) D(6,-2)

19. HALLAR LA PENDIENTE DE:
D(-3,-2) E(5,-2)
HALLAR LA PENDIENTE DE:
Y(2,3) U( 2-1)
Es paralela al eje Ym =
HALLAR LA PENDIENTE DE :
A(-2,3) B(-3,1)

20. HALLAR LA PENDIENTE DE:
X(2,0) Y(4,5)
Hallar la pendiente dé:
c(-1,1) b(1.1)
Hallar la pendiente de :
F(-4,5) G(-4,2)

21. Hallar la pendiente de
S(-2,4) R(1,4)
ANGULO ENTRE DOS RECTAS :
HALLAR EL ANGULO B=
A(5,4) B(-3,3) C( 0,3)
DISTANCIA DE :
AB

22. BC
CA

23. Puntos medios de .
AB
BC
CA

24. PENDIENTE DE LOS PUNTOS
AB
BC
CA

25. ANGULO DE B:
Hallar el angulo de
Siendo las pendientes

26. =31.38
HALLAR EL ANGULO
Hallar el ángulo

27. HALLAR EL ANGULO
HALLAR EL ANGULO

28. HALLAR EL ANGULO

29. HALLAR EL ANGULO

30. HALLAR EL ANGULO
Demostrar que los puntos
A(1,1) B ( 5,3) C (6,-4)
AB

31. 4.47
BC
CA

32. PENDIENTE
A
BC
CA
El ángulo

33. ECUACION DE LA RECTA
PUNTO Y PENDIENTE
Y-Y₁=M(X-X₁)
EJERCICIO 1
ENCUENTRE LA ECUACION DE LA RECTA

34. Ejercicio 2
Encuentre la ecuación de la recta
Y(0,3) m=-2
Remplazando “x “en ecuación

35. X Y
0 3
3 -3
Ejercicio 3
Encuentre la ecuación de la recta
O(5,-3) m=4

36. Encuentre la ecuación de la recta
G(5,4) m =3
Encuentre la ecuación de la recta
S(7,4) m=-4
Encuentre la ecuación de la recta
W(3,2) m:-2

37. Encuentre la ecuación de la recta
H(4,3) m=-1
Encuentre la ecuación de la recta
X(2,4) m=-5

38. Encuentre la ecuación de la recta
Y(2,5) m=3
Encuentre la ecuación de la recta
Z(8,-3) m=2

39. Ecuacion de la recta en
2 puntos conocidos
Ejercicio 1
T(5,3) U(4,9)

40. Ejercicio 2
H(4,3) i(5,8)
Ejercicio 3
U(9,4) v( 5,5)

41. Ejercicio 4
Q(3,6) R(4,7)
Ejercicio 5
A(4,5) B(3,8)

42. Ejercicio 6
Y(9,3) Z(7,5)
Ejercicio 7
S(4,3) R(9,8)

43. Ejercicio 8
K(9,6) l(4,3)
Ejercicio 9
H(2,7) i( 7,6)

44. Ejercicio 10
x(7,5) y( 2,3)
Pendiente y ordenada al origen

45. Hallar la pendiente y ordenada al origen de la ecuación
Hallar la pendiente y ordenada al origen de la siguiente ecuación
Hallar la pendiente y ordenada a l origen

46. Hallar la ecuación sabiendo la m=3 y la ordenada
al origen es 0
M=3 b=0
Hallar la pendiente y la ordenada al origen de la siguiente ecuación
Hallar la Ecuación sabiendo que la pendiente es 7 y la ordenada a la origen es 3
M=7 b=3
En la siguiente ecuación hallar la pendiente y la ordenada al origen:

47. Hallar la pendiente y ordenada al origen
Hallar la pendiente y ordenada al origen

48. Aplicaciones: análisis de pendiente para oferta y demanda.
Oferta, demanda y punto de equilibrio de mercado .punto de
equilibrio de mercado.
La demanda para los bienes está dada para la ecuación:
La oferta esta dada
Sustituyendo p en ecuación (1)

49. El precio es de $3.90 un restaurant en la ciudad atiende 300 almuerzos y cuando el precio es
4.50 solo atiende 100.
x Y
300 3.90
100 4.50

50. En una cafetería en la ciudad de Manabí vende 600 cappuccino al precio de 1,50 y cuando el
precio es de 2,50 solo vende 400
x Y
600 1,5
400 2,5
=-0.005(x-600)
En un restaurante el precio es de $4,50 en la ciudad atiende 400 almuerzos y cuando el
precio es de 5,50 solo atiende 200
x Y
400 4.5
200 5.5

51. No existe demanda de un celular BlackBerry si el precio es de $1700. Por cada disminución
de 100 en su precio la demanda se incrementa en 200 unidades.
Demanda
0 1700
200 1600
Oferta
El fabricante no esta dispuesto a considerar un precio de $500 y ofrecerá 1400 celular
Blackberry al precio de $850
Oferta
Demanda
Oferta
0 500
1400 850

52. b)
hallar el punto de equilibrio
Sustituyendo en ecuacion de oferta
Graficando
x y
4000 -300
3000 200
2000 700

53. 0.25(1000)+500=750
Ys=0.25(0)+500=500
1500 950
x Y
2000 1000
1500 875
1000 750
0 500

54. Una compañía va a entregar 6000 linternas a un precio de $6,00 por unidad si el
precio es de $4,00 por unidad ofrece solo 3000 unidades; determinar la ecuación de
la función de dicha ecuación y grafica la ecuación de oferta.
x Y
6000 6,00
3000 4,00

55. Graficando
y=0.0006+2.4
X Y
10000 3,6
20000 9,6
0 -2,4

56. EN UN RESTAURANTE EL PRECIO ES DE $5.40 EN LA CIUDAD DE MACHALA, ATIENDE
300 ALMUERZOS Y CUANDO EL PRECIO ES DE 6,00 SOLO ATIENDE $200.
X Y
300 5.40
200 6.00
COSTO E INGRESOS LINEALES.EQUILIBRIO DE LA EMPRESA .PERDIDAS Y
GANANCIAS.
EJERCICIO 1

57. LOS COSTOS FIJOS POR PRODUCIR CIERTOS ARTICULOS SON DE $8000 Y LOS COSTOS
VARIABLES SON $4,00 POR UNIDAD
CF=$8000
CV=$4,00 C/U
SI EL PRODUCTOR LOS VNDE A 7 C/U
RESPONDA LO SIGUIENTE :
• Punto de equilibrio
• Determine el numero de unidades que deben venderse al mes para tener una utilidad
de $3000 mensuales.
U=3000
c) x=2000
• Encuentre la perdida cuando solo se producen 2000 unidades al mes, cual es la
utilidad.
A)
EN EL PUNTO DE EQUILBRIO

58. b)
X=3667unidades
c)
Ejercicio 2
Los costos variables de:
Kilo de harina es de $0,30
Costos fijos por día es de $150
• Ecuación del costo lineal y dibuje su grafico.
• Determine el costo de procesar 1500 kilos de azúcar al día.
a)
Costo total: CV +CF
b) sustituyendo1500 en ecuación de costo

59. 450+150=
600
Graficando=
156
=180
x Y
100 180
40 162
20 156
0 150

60. El costo de producir x artículos a la semana
Si cada artículo, puede venderse a o determinar PE.
P=9
PE=?
U=I-C

61. En el PE:
I=9(5000)
Ejercicio
El costo de producir x artículos a la semana
Si cada artículo puede venderse a 3. Determine el punto de equilibrio.
P=3
PE=?
C=7

62. EN EL PUNTO DE EQUILIBRIO.
Ejercicio
El costo de producir x artículos a la semana
Si cada artículo puede venderse a $8,00
Determine el punto de equilibrio.
P=8
Pe=?
En el punto de Equilibrio.

63. Ejercicio
Los costos fijios por producir ciertos artículos son de $8000 y los costos variables de $4,50 por
unidad.
CF=8000
CV=4.50
Si el producto vende c/u a $8,00
Responde lo siguiente.
• Punto de equilibrio.
• Determine el N# de unidades que deben venderse al mes para tener una utilidad de
$2000 mensuales.
P.E
X=?
U=2000
X=1500
Encuentre la perdida cuando solo producen 1500 unidades , al mes ¿Cuál es la utilidad .
A)
U=8X-4.50X-8000
U=3.50X-8000
En el punto de equilibrio

64. EJERCICIO
Costo variables de =
Kilo de arroz es de 0.20
Costo fijo por dia $120
a) Ecuación de l costo lineal y dibuje su grafico.
b) Determine el costo de procesar 1000 kilos de arroz al dia

65. X Ye
0 120
100 240
EL COSTO DE PRODUCIR X ARTICULOS A LA SEMANA
Si c/artículos pueden venderse a 7. Determina P.E

66. En el punto de equilibrio:
Una empresa vende su producto a:
P=50
C(x)=25x+400
• E l nivel de Equilibrio.
• Cuanto deberá producir y vender para tener una ganancia de $3000
X=?
U=3000
c)graficar el punto de Equilbrio.
a)

67. En el Punto de Equilibrio
b)
Graficar: P.E
x Y
0 400
10 650
x Y
0 0
10 500

68. Una fabrica vende su producto a=
P=30
C(x)=20x+800
a) Nivel de Equilibrio
b) Cuanto deberá producir y vender para tener una ganancia de $4000
x=?
u=4000
c) Graficar el punto de Equilibrio.

69. a)
En el punto de Equilibrio.
Ye=30(80)
b)
Graficar P.E
x Y
0 800
10 100

70. b)
x Y
0 0
5 150
10 300
Una empresa vende su producto a:
P=60
C(x)=15x+300
• El nivel de equilibrio
• Cuanto deberá producir y vender para tener una ganancia de $2000
X=?
U=2000
• Graficar el P.E

71. A)
En el Punto de Equilibrio
b)
=51 ARTICULOS
Graficar P.E
15(0)+300
15(10)+300
150+300=450
x Y
0 300
10 450

72. I=60X
I=60(0)=0
I=60(10)=600
x y
0 0
10 600
Unidad 3
Función lineal
Ejercicio 1

73. Ejercicio 2
Ejercicio 3

74. Ejercicio 4
;

75. Ejercicio 5
Ejercicio 6

76. Ejercicio 7
Ejercicio 8

77. Ejercicio 9
Calcule
Ejercicio 10

78. Función Cuadrática. Grafico de una función cuadrática.
Aplicaciones.
Hallar los vértices de:

79. x Y
6 -3
4 -13
0 -9
-4 27
-6 57
=57
Ejercicio 2

80. Ejerccio 3
La utilidad expresada por P(x). Determinar el #u , para maximizar el producto

81. b)40
c)0
EJERCICIO 4
HALLAR LOS VERTICES DE:

82. Ejercicio 5

83. Ejercicio 6
Determine el valor mínimo o máximo según el caso.

84. Ejercicio 7

85. La utilidad expresada por p(x); detremine el numero de unidades para maximizar la producción
La Utilidad expresda por P(x); detremina el numero para maximizar la producción.

86. P(-6)=12x+x²
Operaciones con funciones .composición de factores.
Ejercicio: 1.
Ejercicio 2

87. Ejercicio 3
Ejercicio 4
Ejemplo 5

88. Ejemplo 6
Función exponencial.

89. x Y
3 16
2 4
1 1
0 0.25
-1 0.062
-2 0.015
-3 0.004
Ejercicio 2
0.05

90. x Y
3 0.37
2 0.14
1 0.05
0 0.02
-1 0.007
-2 0.002
Ejercicio 3

92. x Y
3 0.037
1 0.33
0 1
-1 3
-2 9
Ejercicio 4:

93. x Y
3 0.91
2 0.79
1 0.58
0 0.33
-1 0.16
-2 0.07
-3 0.02

94. Ejercicio 5
x Y
2 20.08
1 7.39
0 2.72
-1 1
-2 0.38

95. Ejercicio: 6

96. x Y
3 0.66
2 0.44
1 0.30
0 0.20
-1 0.13
-2 0.087

97. Ejercicio 7:
x Y
3 4.5
2 2
1 0.5
0 0
-1 0.5
-2 2
-3 4.5

98. Ejercicio 8
=14
x Y
4 21
3 14
1 6
0 5
-2 9
-4 21

99. Ejercicio 9

100. x Y
3 2.5
2 -1
1 3.5
0 -5
-1 -5.5
-2 -5
-3 -3.5

101. Ejercicio 10
x Y
3 0
2 -2
1 -2
0 0
-1 4
-2 10
-3 18

102. Funciones logarítmica.
Ejemplo 1
x Y
3 2.20
2 1.39
1 0
-1 0
-2 1.39
-3 2.20

103. Ejemplo2
x Y
3 -21
2 5.45
1 1

104. Ejemplo 3
Ejemplo 4
Ejemplo 5

105. Ejemplo 6
x Y
3 1.04
2 0.83
1 0

106. Ejemplo .7
Ejemplo 8
Ejemplo 9
Ecuaciones logarítmicas y exponenciales.

107. Ejercicio 1
Ejercicio 2
Ejercicio 3