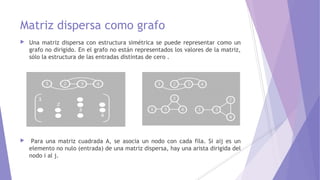
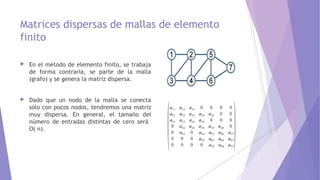
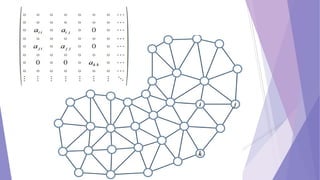
Las matrices dispersas son matrices que contienen muchos ceros, lo que permite usar técnicas especiales para reducir los requerimientos de memoria y el costo de las operaciones. Estas técnicas incluyen almacenar solo los elementos no nulos usando listas enlazadas o vectores, y representar la matriz como un grafo. Las matrices dispersas se usan comúnmente en métodos de elementos finitos donde la conectividad entre nodos es baja.