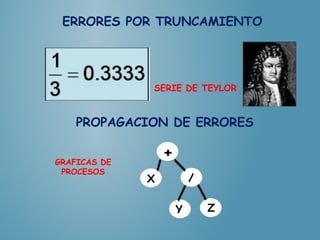
1) Un error es la diferencia entre un valor real y una aproximación a ese valor. Existen diferentes tipos de errores que pueden expresarse de forma absoluta o relativa. 2) Los métodos numéricos producen resultados aproximados que deben especificarse en términos de cifras significativas para indicar su precisión. Errores comunes incluyen errores de redondeo y truncamiento. 3) Para que los métodos numéricos sean útiles en ingeniería, deben ser lo suficientemente exactos para cumplir los requisitos del problema, y lo suficiente

1. UNIVERSIDAD NORORIENTAL PRIVADA
«GRAN MARISCAL DE AYACUCHO»
FACULTAD DE INGENIERA
ESCUELA DE MANTENIMIENTO
NUCLEO EL TIGRE
PROFE: CARLENA ASTUDILLO
BACHILLER:
*MARIN, MERVIS
C.I.: 22.858.355
TEORIA
DE
ERRORES

2. TEORIA DE ERRORES
Un error es una incertidumbre en el resultado de una medida.
Se define como la diferencia entre el valor real Vr y una
aproximación a este valor Va:
e = Vr – Va
Existen diferentes tipos errores, cada uno se puede expresar
en forma absoluta o en forma relativa.

3. APROXIMACION
NUMERICA Y
ERRORES
ERRORES
APROXIMACION
NUMERICA
ARISMETICA DE
LA COMPUTADORA

4. APROXIMACION NUMERICA
APROXIMACION
NUMERICA
3.1416
CIFRAS
SIGNIFICATIVAS
3.1416 NUMEROS DE DIGITOS
EN LA MANTIZA
EXACTITUD
PRECISION
CONVERGENCIA
ESTABILIDAD
SELECCIÓN DE
ALTERNATIVAS

5. ERRORES
ERRORES
ERROR
ABSOLUTO
ERROR
RELATIVO
TIPOS
DE ERRORES
PROPAGACION
DE ERRORES

6. ERRORES HUMANOS
• LECTURA
• TRANSMISION
• TRANSCRIPCION
• PROGRAMACION

7. ERRORES INHERENTES
ERRORES DE REDONDEO
• TRUNCADO
• SIMETRICO

8. ERRORES POR TRUNCAMIENTO
PROPAGACION DE ERRORES
SERIE DE TEYLOR
GRAFICAS DE
PROCESOS
X /
Y Z
+

9. ARISMETICADELA
COMPUTADORA
ARISMETICADELA
COMPUTADORA NUMEROS
ENTEROS
NUMEROS
ENTEROS
NUMEROS
REALES
NUMEROS
REALES
EPSILON DE UNA
COMPUTADORA
EPSILON DE UNA
COMPUTADORA
ARISMETICA DE LA
COMPUTADORA

10. APROXIMACIONES Y ERRORES
DE REDONDEO
HAY DOS ERRORES MAS COMUNES QUE SON:
• Errores de redondeo: se deben a que solo pueden
presentar cantidades con un numero finito de dígitos.
• Errores por truncamiento: representan la diferencia
entre una formulación matemática exacta de un
problema y la aproximación dada por un método
numérico

11. CIFRAS SIGNIFICATIVAS
*El concepto de cifras significativa se ha desarrollado
para designar formalmente la confiabilidad de un valor
numérico
* Las cifras significativas de un numero son aquellas
que puede ser usadas en forma confiables

12. Implicaciones de las cifras significativas en los métodos numéricos
1) Los métodos numéricos obtienen resultados aproximados
•) Se deben desarrollar criterios para especificar que tan precisos
son los resultados
•) Una manera de hacerlo es en términos de cifras significativas
2)Ciertas cantidades representan números específicos , ℮, π, √7,
pero no se pueden expresar exactamente con un numero finito de
dígitos
Ejemplo: π = 3.14178233478785893489…… hasta el infinito

13. EXACTITUS Y PRECISION
• Exactitud: capacidad de un instrumento de acercarse al valor de la
magnitud real. La exactitud es diferente de la precisión.
• Precisión: capacidad de un instrumento de dar el mismo resultado en
mediciones diferentes realizadas en las mismas condiciones. Esta
cualidad debe evaluarse a corto plazo. No debe confundirse con
exactitud ni con reproducibilidad.
•) Inexactitud: Falta de precisión o ajuste de una cosa con otra cosa.
imprecisión. exactitud.
•) Imprecisión: se refiere a la magnitud del esparcimiento de los
valores

14. Los métodos numéricos
deben ser:
• Lo suficiente exactos o
si sesgo para que
cumplan con los
requisitos de un
problema particular de
ingeniería
• los suficientes
precisos para el diseño
de ingeniería

15. Definiciones de errores
• Los errores numéricos se generan con el uso de
aproximaciones para representar las operaciones y
cantidades matemáticas
• Estos incluyen:
• Errores de redondeo: se producen cuando los números tienen
un limite de cifras significativas que se usan para representar
números exactos
• Errores de truncamientos : que resultan de representar
aproximadamente un procedimiento matemático exacto

16. Error absoluto.
Es la diferencia entre el valor de la medida y el valor tomado como exacto.
Puede ser positivo o negativo, según si la medida es superior al valor real o
inferior (la resta sale positiva o negativa). Tiene unidades, las mismas que las de
la medida.
Sin embargo, para facilitar el manejo y el análisis se emplea el error absoluto
definido como:
EA = | P* - P |
Error relativo.
Es el cociente (la división) entre el error absoluto y el valor exacto. Si se
multiplica por 100 se obtiene el tanto por ciento (%) de error. Al igual que el
error absoluto puede ser positivo o negativo (según lo sea el error absoluto)
porque puede ser por exceso o por defecto. no tiene unidades.
Y el error relativo como
ER = | P* - P| / P , si P =/ 0
El error relativo también se puede multiplicar por el 100% para expresarlo
como:
ERP = ER x 100

17. • Estos errores pueden ser relacionados con el numero de
cifras significativas en la aproximación
• Pueden tenerse la seguridad de que el resultado es
correcto en al menos N cifras significativas, si
=(0,50x)%
• De esta forma se debe especificar el valor del error
esperado

18. TEORIA DE ERRORES
SOFTWARE DE COMPUTO NUMÉRICO
Muchas situaciones practicas de la vida real concernientes al campo
de la ingeniería involucran problemas de computo que requieren ser
resueltos empleando ciertos métodos y técnicas matemáticas ,
raíces de polinomios y funciones, soluciones de derivadas e
integrales complicadas, sistemas de ecuaciones , graficas de
funciones, interpolación etc. Las cuales si se llegan a realizar
manualmente llegan a consumir tiempo resultado muy tediosas,
inclusive si seguimos este camino podemos llegar a equivocarnos
debido a la interactividad y complejidad de los métodos

19. EJEMPLOS DE
TEORIA DE ERRORES