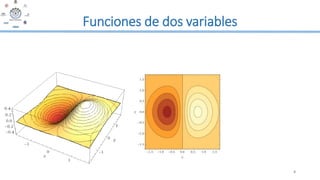
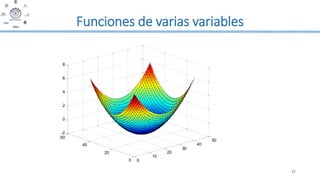
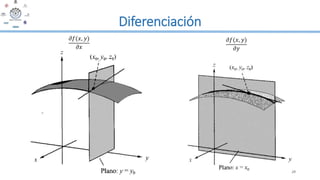
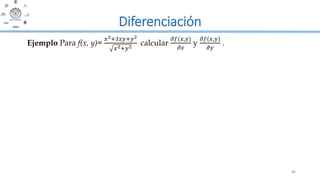
Este documento presenta un módulo sobre cálculo en varias variables. Introduce conceptos como funciones de varias variables, derivadas parciales de primer y segundo orden, y la regla de la cadena para funciones de varias variables. Incluye ejemplos detallados de cómo calcular derivadas parciales y aplicar la regla de la cadena a funciones de dos y tres variables.

1. CURSO PROPEDÉUTICO
MATEMÁTICAS AVANZADAS
Modulo III
Cálculo en varias variables
Octubre 2021

2. Cálculo en varias variables
Contenido del módulo
• Funciones de varias variables.
• Diferenciación.
• Regla de la cadena.
• Extremos.
• Integrales dobles y triples
• Aplicaciones 2

3. Funciones de dos variables
3

4. Funciones de dos variables
4

5. Funciones de dos variables
5
Definición.- Sea D un conjunto de pares ordenados, (x, y) , de números reales tal
que D  R2 . Una función real de dos variables reales es una regla que asigna a cada
par ordenado (x, y) en D un único número real, denotado por f(x, y) . El conjunto D
es llamado el dominio de la función y el conjunto de todos los valores de la función
es el rango de la función.
Cuando tenemos una función de dos variables se suele utilizar z para representar los valores de la función:
z = f (x, y) . La variable z es la variable dependiente y x y y son las variables independientes.

6. Funciones de dos variables
6
Ejemplo. Sea 𝑓 𝑥, 𝑦 = 𝑦 + 4𝑥2 − 4
a) Calcular el dominio de f.
b) Represéntelo gráficamente.
c) Calcule f (2, 0), 𝑓(−
2
2
, 2) y f (1, -1)

7. Funciones de dos variables
7

8. Funciones de dos variables
8

9. Funciones de dos variables
9

10. Funciones de dos variables
10

11. Funciones de dos variables
11

12. Funciones de dos variables
12

13. Funciones de dos variables
13

14. Funciones de dos variables
14

15. Funciones de dos variables
15
Ejemplo Encuentre el dominio de la siguientes funciones y represéntelas
gráficamente.
a) f (x, y) = ln(4 - 2y +x)
b) f(x,y) =
𝑥
𝑥+𝑦

16. Funciones de dos variables
16

17. Funciones de dos variables
17

18. Funciones de dos variables
18

19. Funciones de dos variables
19

20. Funciones de dos variables
20

21. Funciones de dos variables
21

22. Funciones de dos variables
22

23. Funciones de dos variables
23

24. Funciones de varias variables
24
Definición (Función de varias variables) Sea D un subconjunto de
Rn . Si a cada (x1, . . . , xn)  D le corresponde un único número
real
f (x1, . . . , xn)
se dice que f es una función de las variables x1, . . . , xn.

25. Funciones de varias variables
25
Ejemplo Encuentre el dominio de la siguiente función y represéntela
gráficamente.
f (x, y, z) = ln(1 - x2 – y2 + z)

26. Funciones de varias variables
26

27. Funciones de varias variables
27
0
10
20
30
40
50
0
20
40
60
-2
0
2
4
6
8

28. Diferenciación
28
Derivadas parciales
Definición.- Sea f una función en las variables x y y. La derivada
parcial de f con respecto a x está definida por
𝜕𝑓(𝑥, 𝑦)
𝜕𝑥
= lim
ℎ→0
𝑓 𝑥 + ℎ, 𝑦 − 𝑓(𝑥, 𝑦)
ℎ
siempre y cuando este límite exista.
La derivada parcial de f con respecto a y está definida por.
𝜕𝑓(𝑥, 𝑦)
𝜕𝑦
= lim
ℎ→0
𝑓 𝑥, 𝑦 + ℎ − 𝑓(𝑥, 𝑦)
ℎ
siempre y cuando este límite exista.

29. 29
Diferenciación
𝜕𝑓(𝑥, 𝑦)
𝜕𝑥
𝜕𝑓(𝑥, 𝑦)
𝜕𝑦

30. 30
Diferenciación

31. 31
Ejemplo Para f(x, y)= 3x2- 4xy + 5y3 calcule
𝜕𝑓(𝑥,𝑦)
𝜕𝑥
y
𝜕𝑓(𝑥,𝑦)
𝜕𝑦
usando la definición.
Diferenciación

32. 32
Diferenciación

33. 33
Diferenciación

34. 34
Diferenciación

35. 35
Diferenciación
Ejemplo Para f(x, y)= x2y3 calcule
𝜕𝑓(𝑥,𝑦)
𝜕𝑥
y
𝜕𝑓(𝑥,𝑦)
𝜕𝑦
usando la definición.

36. 36
Diferenciación

37. 37
Diferenciación

38. 38
Diferenciación

39. 39
Diferenciación

40. 40
Diferenciación

41. 41
Diferenciación
Ejemplo Para f(x, y)=
𝑥2+3𝑥𝑦+𝑦2
𝑥2+𝑦2
calcular
𝜕𝑓(𝑥,𝑦)
𝜕𝑥
y
𝜕𝑓(𝑥,𝑦)
𝜕𝑦
.

42. 42
Diferenciación

43. 43
Diferenciación
Ejemplo Para f(x, y, z)=
𝑥2+𝑦2
𝑧(𝑥+𝑦)
calcular
𝜕𝑓(𝑥,𝑦,𝑧)
𝜕𝑥
,
𝜕𝑓(𝑥,𝑦,𝑧)
𝜕𝑦
,
𝜕𝑓(𝑥,𝑦, 𝑧)
𝜕𝑧
.

44. 44
Diferenciación
Si f es una función en las variables x y y entonces, en general, las derivadas
parciales son funciones también de x y y , y por tanto se puede calcular su
derivada tanto para x como para y. Estas derivadas se llaman segundas
derivadas parciales de f y son cuatro en total.
Derivadas de orden superior
𝜕2
𝑓
𝜕𝑥2
=
𝜕
𝜕𝑥
𝜕𝑓(𝑥, 𝑦)
𝜕𝑥
𝜕2
𝑓
𝜕𝑦2
=
𝜕
𝜕𝑦
𝜕𝑓(𝑥, 𝑦)
𝜕𝑦
𝜕2𝑓
𝜕𝑥𝜕𝑦
=
𝜕
𝜕𝑥
𝜕𝑓(𝑥, 𝑦)
𝜕𝑦
𝜕2
𝑓
𝜕𝑦𝜕𝑥
=
𝜕
𝜕𝑦
𝜕𝑓(𝑥, 𝑦)
𝜕𝑥

45. 45
Diferenciación
Ejemplo. Encuentre las derivadas de segundo orden de f (x, y) = x2 y4 + e3x .

46. 46
Diferenciación

47. 47
Diferenciación

48. 48
Diferenciación

49. 49
Diferenciación
Ejemplo. Encuentre
𝜕3𝑓
𝜕𝑧𝜕𝑦𝜕𝑥
si f (x, y, z) = x2 y4z2+xyzln(x).

50. 50
Diferenciación

51. 51
Diferenciación

52. 52
Diferenciación

53. 53
Regla de la cadena
Para derivar funciones compuestas de una sola variable podíamos usar la regla de la
cadena. Si y = f (x) y x a su vez es una función de t, entonces podíamos pensar a y como
función de t y para calcular su derivada lo podíamos hacer directamente por la regla
de la cadena:
𝑑𝑦
𝑑𝑡
=
𝑑𝑦
𝑑𝑥
𝑑𝑥
𝑑𝑡
Para una sola variable

54. 54
Regla de la cadena
Regla de la cadena (caso 1) Sea z = f (x, y) función con derivadas parciales continuas y
x= x(t) y y = y(t) funciones derivables. Entonces z = f (x(t), y(t)) es derivable en t y
𝑑𝑧
𝑑𝑡
=
𝜕𝑧
𝜕𝑥
∙
𝑑𝑥
𝑑𝑡
+
𝜕𝑧
𝜕𝑦
∙
𝑑𝑦
𝑑𝑡
Para una varias variables

55. 55
Regla de la cadena
Ejemplo. Sean z = y2 𝑥 + 1 donde x(t)= t3- t y y(t)= t2 -2t +4 . Encontrar
𝑑𝑧
𝑑𝑡

56. 56
Regla de la cadena

57. 57
Regla de la cadena

58. 58
Regla de la cadena

59. 59
Regla de la cadena

60. 60
Regla de la cadena
Regla de la cadena (caso 2) Sea z = f (x, y) función con derivadas parciales continuas en
sus variables y x= x(u,v) y y = y(u,v) funciones derivables. Entonces z = f (x(u, v), y(u,
v)) es derivable en u y v con
𝑑𝑧
𝑑𝑢
=
𝜕𝑧
𝜕𝑥
∙
𝜕𝑥
𝜕𝑢
+
𝜕𝑧
𝜕𝑦
∙
𝜕𝑦
𝜕𝑢
𝑑𝑧
𝑑𝑣
=
𝜕𝑧
𝜕𝑥
∙
𝜕𝑥
𝜕𝑣
+
𝜕𝑧
𝜕𝑦
∙
𝜕𝑦
𝜕𝑣
Para varias variables

61. 61
Regla de la cadena
Ejemplo. Sean z = ex-3y, donde x(u, v)=vu3 - v y y(u, v)= u – 4v .
Encontrar
𝜕𝑧
𝜕𝑢
𝑦
𝜕𝑧
𝜕𝑣

62. 62
Regla de la cadena

63. 63
Regla de la cadena

64. 64
Regla de la cadena

65. 65
Regla de la cadena

66. 66
Regla de la cadena

67. Gracias por su atención
67