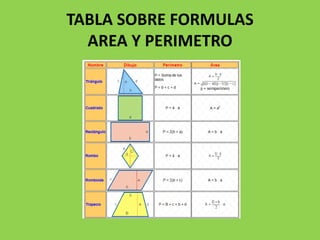
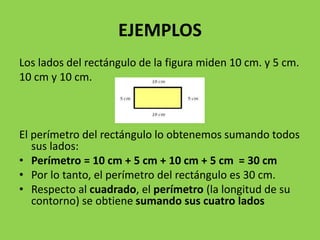
Este documento presenta información sobre el perímetro y área de figuras geométricas. Explica que el perímetro es la suma de los lados de una figura, mientras que el área es la cantidad de superficie interior. Proporciona ejemplos de cálculos de perímetro y área para figuras como rectángulos, triángulos y cuadrados. También incluye una tabla con fórmulas de perímetro y área y ejercicios de evaluación para practicar los conceptos. El objetivo es mejorar la comprensión de estas medidas en fig

1. UNIVERSIDAD AUTONOMA DE BAJA
CALIFORNIA
FACULTAD DE PEDAGOGIA E INOVACION E.
PAOLA RAQUEL IRIARTE MEJIA
MEXICALI B.C A 15 DE ENERO DEL 2016

2. ÍNDICE TEMÁTICO
• Introducción
• Ejemplos
• Evaluación
• Objetivo
• Conclusion
• Referencias bibliográficas

3. INTRODUCCION
La palabra perímetro proviene del latín perimĕtros, que a su
vez deriva de un concepto griego. Más concretamente
podemos explicar que en su origen etimológico griego nos
encontramos con el hecho de que este término está
conformado por dos partes perfectamente diferenciadas.
Así, en primer lugar, está el prefijo peri– que puede
traducirse como sinónimo de “alrededor” y, en segundo
lugar, se encuentra el vocablo metron que es equivalente a
“medida”.
Se refiere al contorno de una superficie o de una figura y a
la medida de ese contorno.
En otras palabras, en una figura, el perímetro es la suma de
todos sus lados.

4. INTRODUCCION
Para calcular el perímetro de una
superficie, es necesario conocer la
longitud de todos sus lados.
Ejemplo: un cuadrado cuyos ambos
lados miden 4 cm , su perimetro
sera de 16 cm.
El perímetro también puede
permitir, en ocasiones, conocer
el dato desconocido de un lado.

5. INTRODUCCION
Consideraremos como una
definición de área, a aquella
cantidad de superficie que
se encuentra encerrada
dentro de una figura
geométrica cerrada. El área
es la que posibilita el
conocimiento de la
superficie interior.

6. TABLA SOBRE FORMULAS
AREA Y PERIMETRO

7. EJEMPLOS
Los lados del rectángulo de la figura miden 10 cm. y 5 cm.
10 cm y 10 cm.
El perímetro del rectángulo lo obtenemos sumando todos
sus lados:
• Perímetro = 10 cm + 5 cm + 10 cm + 5 cm = 30 cm
• Por lo tanto, el perímetro del rectángulo es 30 cm.
• Respecto al cuadrado, el perímetro (la longitud de su
contorno) se obtiene sumando sus cuatro lados

8. EJEMPLOS
Hallar el área del siguiente triángulo:
A = 52 = 25 cm2
Calcular el área de un cuadrado de 5 cm de
lado.

9. EVALUACION
1) Calcular el área y el perímetro de un rombo
cuyas diagonales miden 30 y 16 cm, y su lado
mide 17 cm.
2) Calcula el perímetro y el área de un rombo cuyas
diagonales miden 8 cm y 6 cm respectivamente.
3) Calcula el lado de un rombo cuyo perímetro
mide 40 cm.
4) Calcula el perímetro y el área de un rombo cuyo
lado mide 10 cm y la diagonal mayor 16 cm.

10. OBJETIVO
El objetivo de este OA , es hacer que los
alumnos de nivel secundario conozcan un
poco de áreas y perímetros sobre figuras
geométricas, logran una mejor comprensión y
cumplir todo lo que un OA debe cumplir en
cuanto a su función y sus características.

11. CONCLUSION
Con la creación de este OA pretendí hacer un
poco mas divertido y atractivo el resolver
problemas geométricos, también ser un poco
practica y clara en cuanto a la información que
se plasmo, al momento de dar la introducción
utilice un lenguaje comprensible y claro, de
acuerdo al tipo de nivel educativo que
estamos tratando.

12. REFERENCIAS BIBLIOGRAFICAS
• https://recursospcpi.files.wordpress.com/201
1/04/perc3admetros-y-c3a1reas-de-figuras-
planas-ejercicios.pdf
• http://www.vitutor.net/2/1/0.html
• LIBRO MATEMATICAS , EDITORIAL SEP 1 DE
SECUNDARIA.