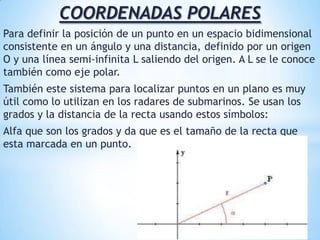
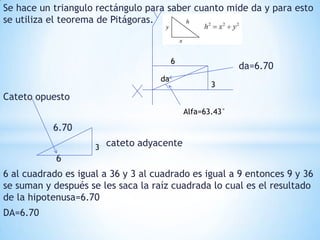
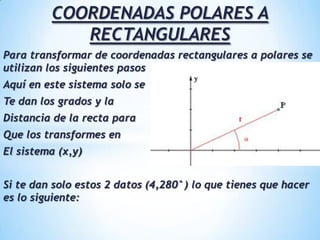
Este documento explica las coordenadas rectangulares y polares. Describe cómo las coordenadas rectangulares localizan un punto usando un par de números (x,y) y cómo las coordenadas polares usan un ángulo y una distancia (da, alfa). También detalla cómo transformar entre los dos sistemas de coordenadas usando el teorema de Pitágoras y funciones trigonométricas y proporciona ejemplos y ejercicios.

1. COORDENADAS RECTANGULARES Y POLARESRicardo González Mancilla 372B

2. CONTENIDOSExplicacion del contenido……………………………………………………3Coordenadas rctangulares…………………………………………………..4Coordenadas polares…………………………………………………………….6Transformacion de coordenadas rectangulares a polares..7Polares a rectangulares…………………………………………………………10Ejercicios………………………………………………………………………………….12Referencias………………………………………………………………………….....14

3. EXPLICACION DEL CONTENIDOEn estos temas de coordenadas rectangulares y polares se les dará información de que es lo que son, su localización en un plano, para lo que son útiles y como se pueden transformar coordenadas rectangulares a polares y viceversa. También para que lo pongas en practica se te darán ejercicios para resolver con su respectiva respuesta y para mayor comprensión también habrá formulas claras y para que puedas corroborar y aumentar tus conocimientos sobre estos temas se te proporcionaran los libros que fueron consultados para elaborar esta explicación sobre estos 2 temas.

4. COORDENADAS RECTANGULARESEn un sistema de coordenadas rectangulares o cartesiano se puede localizar un punto con una sola pareja de puntos (x,y) estos valores son las distancias dirigidas, partiendo del origen, desde los ejes x e y respectivamente. El origen es el punto donde se intersectan los dos ejes coordenados. En un par de números (x,y) en el cual «x» es el primer numero y «y» el segundo se llama pareja ordenada. Se traza una recta horizontal y una vertical que se cortan en el origen 0 y con una medida conveniente se hace una escala de números reales en cada eje coordenado dejando que el origen sea (0,0).La dirección positiva se escoge haciaLa derecha en el eje x y hacia arriba en elEje y.

5. L a coordenada x, o abscisa, de un punto p es la distancia dirigida desde el eje y hasta el punto. La coordenada y u ordenada de un punto p es la distancia desde el eje x hacia el punto.Un punto de coordenadas dadas se marca midiendo las distancias apropiadas desde los ejes y señalando el punto así localizado. Por ejemplo si las coordenadas de un punto son (-4,3) la abscisa -4 significa que el punto esta 4 unidades a ala izquierda del eje y contando desde el origen y la ordenada 3 significa que el punto esta 3 unidades hacia arriba del eje x contando desde el origen.43

6. COORDENADAS POLARESPara definir la posición de un punto en un espacio bidimensional consistente en un ángulo y una distancia, definido por un origen O y una línea semi-infinita L saliendo del origen. A L se le conoce también como eje polar.También este sistema para localizar puntos en un plano es muy útil como lo utilizan en los radares de submarinos. Se usan los grados y la distancia de la recta usando estos símbolos: Alfa que son los grados y da que es el tamaño de la recta que esta marcada en un punto.

7. TRANSFORMACION DE COORDENADAS RECTANGULARES A POLARES Y VICEVERSAPara transformar de coordenadas rectangulares a polares se utilizan los siguientes métodos.

8. Se hace un triangulo rectángulo para saber cuanto mide da y para esto se utiliza el teorema de Pitágoras. da=6.70Cateto opuesto 6.70 cateto adyacente 66 al cuadrado es igual a 36 y 3 al cuadrado es igual a 9 entonces 9 y 36 se suman y después se les saca la raíz cuadrada lo cual es el resultado de la hipotenusa=6.70DA=6.70 6da3Alfa=63.43°3

9. Ya se a sacado el valor de da y solo falta el valor de los grados ósea alfa en el cual se utiliza la siguiente formula: Alfa=Tan-1 (cateto opuesto sobre cateto adyacente) Alfa=Tan-1(6/3) Alfa=63.43° da=6.70 Rectangulares Polares A (X,Y) A(da, Alfa) (6,3) (6.70,63.43°)

10. COORDENADAS POLARES A RECTANGULARESPara transformar de coordenadas rectangulares a polares se utilizan los siguientes pasosAquí en este sistema solo seTe dan los grados y laDistancia de la recta para Que los transformes enEl sistema (x,y)Si te dan solo estos 2 datos (4,280°) lo que tienes que hacer es lo siguiente:

11. Se utilizan estas 2 funciones: hipotenusa Sen=cateto opuesto (c.o) hipotenusa Cos=cateto adyacente (c.a) 4 Sen 280°=-3.93 4 Cos 280°=0.69 (0.69, -3.93) (X,Y) 280° - 3.93 4 0.69Con la función de seno se saca el punto en el eje de la y y con la de coseno el eje de las x.

12. EJERCICIOSUn pirata que habita en una isla quiere encontrar un tesoro y la ubicación que le dio su capitán en coordenadas rectangulares fue (6,10) pero el solo identifica puntos en coordenadas polares. Así que ayuda al pirata transformando las coordenadas rectangulares a polares. 6 (6x6)+(10x10)= 136=11.6 da=11.6 da 10Alfa=Tan-1 (10/6)=59.03°Alfa=59.03° Alfa(11.6,59.03°)

13. A un soldado que viajaba en un submarino su teniente le ordeno que al desembarcar la costa seria su punto de origen y que tendría que llegar a la base militar que estaba en (10,100°) se la dio en coordenadas polares puesto que el teniente vio en su radar de submarino las coordenadas pero el soldado no sabe cambiar coordenadas polares a rectangulares así que ayundelo a cambiarlas. 10 Cos 100°=-1.73 10 10 Sen 100°=9.84 9.84 100° -1.73 (-1.73,9.84)

14. REFERENCIASGeometría Analítica de FullerEditorial: ADDISON WESLEY PUBLISHING COMPANY.Matemáticas 3 bachillerato de Patricia Mata HolguínEditorial: ST editorialGeometría Analítica de Arquímedes Caballero C., Lorenzo Martínez C., Jesús Bernárdez G.Editorial: Esfinge