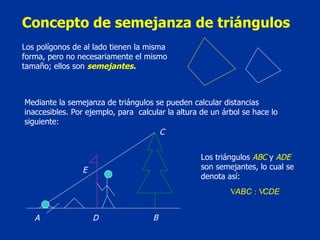
El documento describe la semejanza de triángulos y cómo se puede usar para calcular distancias inaccesibles mediante proporciones. Explica que dos triángulos son semejantes si sus ángulos correspondientes tienen la misma medida y sus lados correspondientes son proporcionales. Luego presenta varios ejemplos de cómo calcular alturas, distancias y otras medidas usando la propiedad de semejanza de triángulos.

1. Departamento de Matemáticas Universidad Católica Los Ángeles de Chimbote - Arequipa (Versión preliminar) Triángulos semejantes Mg. Augusto Fernández H.

2. Los polígonos de al lado tienen la misma forma, pero no necesariamente el mismo tamaño; ellos son semejantes . Mediante la semejanza de triángulos se pueden calcular distancias inaccesibles. Por ejemplo, para calcular la altura de un árbol se hace lo siguiente: A E D C B Los triángulos ABC y ADE son semejantes, lo cual se denota así: Concepto de semejanza de triángulos

3. Al separar los triángulos de la figura anterior se tiene lo siguiente: En ellos se tiene: A E D C B A Dado que las longitudes en el piso y la longitud en el asta se pueden medir, entonces usando una de las proporciones anteriores se obtiene la altura del árbol. Observe:

4. Dos triángulos son semejantes , si sus ángulos correspondientes tienen la misma medida y si sus lados correspondiente son proporcionales. F E D C B A Supóngase que Entonces, se tiene En la semejanza de triángulos; la igualdad de las medidas de los ángulos, define una correspondencia entre los vértices, los ángulos y entre los lados de los triángulos. Dichas correspondencias se denotan con una flecha de doble punta , lo cual se lee “se corresponde con”. Observe:

5. La sombra que una persona proyecta al alejarse de un farol es 1/3 de su distancia al poste del farol. Si la persona mide 1.70 m y la punta de la sombra dista de dicho poste 12 m, ¿qué altura tiene el farol y qué longitud tiene la sombra? Un topógrafo desea medir el ancho de una montaña, por donde se pretende hacer un túnel desde un punto A hasta un punto B , opuesto a ella y visibles ambos desde un punto C en la llanura, como se muestra en la figura adjunta. Para ello él localiza los puntos D y E de modo que Calcule la longitud del túnel.

6. Se dispone de dos tirantes, uno de 30 m y otro de 25 m, para contener un puente de 33 m de largo como se muestra en la figura adjunta, en donde . Entonces: ¿A qué distancia está el punto C de las bases de los postes ? Si , ¿cuánto mide el poste ?. 3 1 D C B A ¿Cuál de los segmentos de la figura mide ?

7. Dos triángulos son semejantes , si dos ángulos de uno miden lo mismo que dos ángulos del otro. Si la razón de los lados correspondientes es uno, los triángulos son congruentes . D C B A E Si , ¿son semejantes los triángulos ABC y DEC ? D C B A E F El símbolo de congruencia es y se lee “ es congruente con”. porque:

8. D C B A O Si y O es punto medio de , ¿son congruentes los triángulos AOB y COD ?

9. Fin