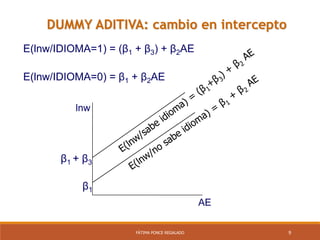
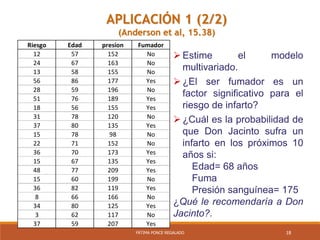
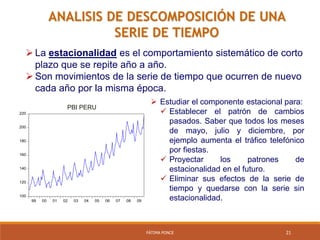
Este documento presenta los métodos de regresión con variables dicotómicas (dummy). Explica el uso de variables dummy, y tres modelos con variables dummy: modelo con dummy aditiva, modelo con dummy multiplicativa y modelo con dummy de interacción. Además, presenta ejemplos y aplicaciones de estos modelos, incluyendo la captura de quiebres estructurales y el análisis de series de tiempo con componente estacional usando variables dummy estacionales.

1. MÉTODOS DE INVESTIGACIÓN
CUANTITATIVA
Sesión 12
REGRESIÓN CON VARIABLES DICOTÓMICAS
FÁTIMA PONCE REGALADO 1

2. 2
PUNTOS A TRATAR
FÁTIMA PONCE REGALADO
REGRESIÓN CON VARIABLES DICOTÓMICAS
Uso de las variables dummy
Modelos con variables dicotómicas.
oModelo con Dummy Aditiva.
oModelo con Dummy Multiplicativa.
oModelo con Dummy Interacción.
Aplicaciones

3. 3FÁTIMA PONCE REGALADO
 Las dummy (o cualitativas, binarias, dicotómicas ó ficticias)
se diferencian de las variables cuantitativas porque toman
valores discretos:
1 =presencia de la categoría o cualidad,
0 =ausencia de la categoría o cualidad
 Recogen el efecto de las variables cualitativas
independientes sobre la variable dependiente. Ejemplo:
Sexo, procedencia geográfica, nivel de educación, idiomas,
región, efecto de una norma, quiebre estructural, etc.
 Dummy como variable independiente.
VARIABLES DICOTÓMICAS
(DUMMY o FICTICIAS)

4. 4FÁTIMA PONCE REGALADO
MODELOS CON VARIABLES DICOTÓMICAS
Ejemplo: Se desea explicar el salario (w) en relación a las
variables Años de Experiencia (AE) e Idiomas (IDIOMA).
1 sabe idiomas
IDIOMA 0 no sabe idiomas
Con Dummy aditiva (cambio en intercepto).
w = β1 + β2 AE + β3 IDIOMA + µ ,
Con Dummy multiplicativa (cambio en pendiente)
w = β1 + β2 AE + β3 IDIOMA*AE + µ

5. 5FÁTIMA PONCE REGALADO
DUMMY ADITIVA
(o cambio en intercepto)

6. 6FÁTIMA PONCE REGALADO
categoría base
(elección es arbitraria)
Se plantea el siguiente modelo:
1 si estudiante emplea PC
PC 0 si no emplea PC
uniNota)= Nota en la universidad
notaSEC= Nota en secundaria
notaPrueba = Nota de la prueba
uniNota = 1 + 2 PC + 3notaSEC + 4notaPrueba + 
MODELO CON DUMMY ADITIVA
Ejemplo 1: Efecto de usar PC sobre la nota

7. 7FÁTIMA PONCE REGALADO
Se obtuvo la siguiente estimación:
El estudiante que emplea PC en promedio tiene
cerca de 1 punto más que un estudiante que no
emplea PC.
^
El t2=3.3  variable dummy es relevante
estadísticamente.
^
uniNota= 6.3 + 0.99PC + 2.235 notaSEC + 0.47notaPrueba
(1.65) (0.30) (0.47) (0.0525)
n=141, R2=0.289
MODELO CON DUMMY ADITIVA
Ejemplo 1: Efecto de usar PC sobre la nota

8. 8FÁTIMA PONCE REGALADO
MODELO CON DUMMY ADITIVA
Ejemplo 2: Efecto de saber otro IDIOMA sobre el salario
Se plantea el modelo:
lnw = β1 + β2 AE + β3 IDIOMA + µ ,
w=salario AE = Años de experiencia.
1 sabe idiomas
IDIOMA 0 no sabe idiomas
Interpretación:
E(lnw/IDIOMA=1) = β1 + β2AE + β3 = (β1 + β3) + β2AE
E(lnw/IDIOMA=0) = β1 + β2AE
>0
 Para saber si es estadísticamente relevante la diferencia del
salario por IDIOMA se debe
^ ^
evaluar el t de β3 ó su probabilidad (p-valor).

9. 9FÁTIMA PONCE REGALADO
E(lnw/IDIOMA=1) = (β1 + β3) + β2AE
E(lnw/IDIOMA=0) = β1 + β2AE
β1
β1 + β3
lnw
AE
DUMMY ADITIVA: cambio en intercepto

10. 10FÁTIMA PONCE REGALADO
Suponga que se tiene el siguiente modelo:
ln salario = 1 + 2 educ + 3 género+ 
Modelo con Dummy Aditiva
Ejemplo 3: Diferenciación Salarial por Género
3 es la diferencia del salario entre hombres y
mujeres, dada la misma cantidad de educación (los
mismos años de estudio).
3=E(lnsalario/hombre,educ) - E(lnsalario/mujer,educ)
Si 3 > 0  para el mismo nivel de los otros factores
los hombres ganan en promedio más que las mujeres.
1 si hombre
género 0 si mujer

11. 11FÁTIMA PONCE REGALADO
DUMMY MULTIPLICATIVA
(o cambio en pendiente)

12. 12FÁTIMA PONCE REGALADO
DUMMY MULTIPLICATIVA: cambio en pendiente
Se desea explicar el salario con efecto en la pendiente
(tasa salarial).
ln w = β1 + β2 AE + β3 IDIOMA*AE + µ
AE = Años de experiencia.
1 sabe idiomas
IDIOMA 0 no sabe idiomas
E(lnw/IDIOMA=1) = β1 + β2AE + β3AE = β1 + (β3+β2)AE
E(lnw/IDIOMA=0) = β1 + β2AE
 Para saber si es estadísticamente relevante la diferencia del sa-
^ ^
lario por IDIOMA se debe evaluar el t de β3 ó su p-valor.

13. 13FÁTIMA PONCE REGALADO
DUMMY INTERACCIÓN

14. FÁTIMA PONCE 14
DUMMY INTERACCION (1/2)
 Si se tiene más de una variable dummy como regresor por
ejemplo en la función de salarios, se tiene Sexo (H-M) e
Idioma (Ingés-No inglés) :
W = 1 + 2 AE + 3DS+ 4 DI
 Puede haber efecto interacción entre 2 variables
cualitativas: Sexo e Idioma y su efecto no es solo aditivo
o multiplicativo sino:
W = 1 + 2 AE + 3DS+ 4 DI + 5(DS *DI)
E(W/DS=1, DI=1, AE) : (1+3+ 4+5) + 2AE

15. FÁTIMA PONCE 15
DUMMY INTERACCION (2/2)
Si el modelo es:
W = 1 + 2D2 + 3D3+ 4 D2D3 + 5X + 
W= salario por hora en dólares
X= años de educación
D2= 1 si mujer, o de otra manera
D3= 1 si no blanca/no hispánica, 0 de otra manera
efecto diferencial de ser mujer
no blanca / no hispánica

16. 16FÁTIMA PONCE REGALADO
APLICACIONES

17. 17FÁTIMA PONCE REGALADO
APLICACIÓN 1 (1/2)
(Anderson et al, 15.38)
Un estudio realizado a lo largo de 10 años por la American
Heart Association proporcionó datos sobre la relación que
tienen la edad, la presión sanguínea y el fumar sobre el
riesgo de sufrir un infarto. Los datos están en el archivo
Fumador.xlsx pase los datos a Eviews y trabaje con dicho
software.
El riesgo se interpreta como la probabilidad (multiplicada
por 100) de que el paciente sufra un infarto en los
próximos 10 años.
1 si la persona fuma
Fumador: 0 si la persona no fuma

18. 18FÁTIMA PONCE REGALADO
APLICACIÓN 1 (2/2)
(Anderson et al, 15.38)
Riesgo Edad presion Fumador
12 57 152 No
24 67 163 No
13 58 155 No
56 86 177 Yes
28 59 196 No
51 76 189 Yes
18 56 155 Yes
31 78 120 No
37 80 135 Yes
15 78 98 No
22 71 152 No
36 70 173 Yes
15 67 135 Yes
48 77 209 Yes
15 60 199 No
36 82 119 Yes
8 66 166 No
34 80 125 Yes
3 62 117 No
37 59 207 Yes
 Estime el modelo
multivariado.
 ¿El ser fumador es un
factor significativo para el
riesgo de infarto?
 ¿Cuál es la probabilidad de
que Don Jacinto sufra un
infarto en los próximos 10
años si:
Edad= 68 años
Fuma
Presión sanguínea= 175
¿Qué le recomendaría a Don
Jacinto?.

19. FÁTIMA PONCE 19
CAPTURANDO QUIEBRE ESTRUCTURAL
 Si el cambio afecta intercepto y pendientes  El modelo debe
emplear dummy aditiva y dummy multiplicativa:
Y = β1 + β2 X2 + β3 X3 + β4 DQ + β5 (X2*DQ) + β6 (X3*DQ) + µ ,
1 si quiebre
DQ
0 no quiebre
E(Y/DQ=1)= (β1+β4) + (β2+β5) X2 + (β3+β6) X3
E(Y/DQ=0) = β1 + β2X2 + β3 X3
 Para saber si el efecto del quiebre es estadísticamente relevante en el
^ ^ ^ ^ ^ ^
intercepto y las pendientes  Evaluar t de β4, t de β5 y t de β6 o sus
p-valor.

20. FÁTIMA PONCE 20
DUMMY ESTACIONAL (1/2)
 De acuerdo al Modelo Clásico General de Análisis de
Descomposición de las Series de Tiempo, toda serie está
compuesta de:
 Tendencia (T): Componente a largo plazo.
 Estacionalidad (E), si la periodicidad de la serie es inferior a
1 año. Patrón de cambio que ocurre periódicamente.
 Ciclo (C): Fluctuación o dinámica que no es explicada ni por
la tendencia ni por la estacionalidad.
 Componente irregular (I): Variabilidad debido al azar que se
observa después de retirar los otros componentes.

21. FÁTIMA PONCE 21
 La estacionalidad es el comportamiento sistemático de corto
plazo que se repite año a año.
 Son movimientos de la serie de tiempo que ocurren de nuevo
cada año por la misma época.
ANALISIS DE DESCOMPOSICIÓN DE UNA
SERIE DE TIEMPO
 Estudiar el componente estacional para:
 Establecer el patrón de cambios
pasados. Saber que todos los meses
de mayo, julio y diciembre, por
ejemplo aumenta el tráfico telefónico
por fiestas.
 Proyectar los patrones de
estacionalidad en el futuro.
 Eliminar sus efectos de la serie de
tiempo y quedarse con la serie sin
estacionalidad.100
120
140
160
180
200
220
99 00 01 02 03 04 05 06 07 08 09
PBI
PBI PERU

22. FÁTIMA PONCE 22
DUMMY ESTACIONAL (1/3)
 Ejemplo de Jhonston&Dinardo pg. 134: Modelo Inicial de
Gasto en Vacaciones:
Yt = 1 + xt’β + µt data trimestral
Qit = 1 si observación esta en el trimestre i
0 de otra manera.
Para i = 1,…, 4 para los 4 trimestres de cada año las dummies son:
Q1 Q2 Q3 Q4
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1

23. FÁTIMA PONCE 23
DUMMY ESTACIONAL (2/3)
 Modelo: Yt = 1 + 2Q 2 t + 3Q 3 t + 4Q 4 t + xt’β + µt
Para evaluar estacionalidad en la función:
H0: 2 = 3 = 4 = 0 (No hay estacionalidad relevante)
Emplear un test de hipótesis conjunto: F
Si Fest< Ftabla ó p-valor>0.05  Aceptar H0, no hay estacionalidad.
Si Fest > Ftabla ó p-valor<0.05 Aceptar H1, la estacionalidad es
relevante.

24. FÁTIMA PONCE 24
DUMMY ESTACIONAL (3/3)
Para evaluar la relevancia de la estacionalidad en un trimestre
en particular se analiza el estadístico test correspondiente:
Modelo: Yt = 1 + 2Q 2t + 3Q 3t + 4Q 4t + xt’β + µt
Para evaluar estacionalidad en un trimestre:
H0: 2 = 0 (No hay estacionalidad relevante en T.II)
Si test< ttabla ó p-valor>0.05  Aceptar H0, no hay
estacionalidad relevante en ese trimestre.
Si test> ttabla ó p-valor<0.05  Aceptar H1, estacionalidad del T.II
es relevante.

25. 25FÁTIMA PONCE REGALADO
Anderson, D., Sweeney, D. y Williams T. (2008). Estadística
para Administración y Economía. [10ma. Ed.] México,
Cengage Learning Editores S.A. de C.V., Cap 14 y 15.
Levin, R. y Rubin, D. (2010). Estadística para Administración
y Economía. Séptima Edición Revisada. Pearson Educación,
México. Prentice Hall. 2010. Cap. 12 y 13.
BIBLIOGRAFIA