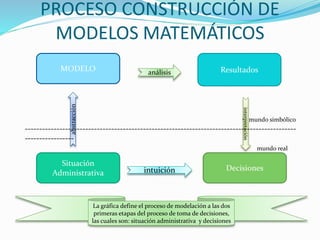
El documento discute la importancia de los modelos matemáticos en la educación y su aplicación en la resolución de problemas reales. Destaca la labor del Centro Multidisciplinario de Modelación Matemática y Computacional (CEMMAC) en Puebla, que integra la matemática con otras disciplinas para abordar problemas en neurociencias, cardiología y epidemiología. Además, enfatiza la necesidad de mejorar la enseñanza de las matemáticas desde niveles básicos para desarrollar el pensamiento lógico en los estudiantes.

1. DIEGO LEANDRO IZA GAVILANES
Tutor
Msc. ACOSTA BONILLA JHON PATRICIO
Tarea
MODELO MATEMATICO, SU
CLASIFICACION, LA CONSTRUCCIÓN
DE MODELOS MATEMÁTICOS Y LA
RESOLUCIÓN DE PROBLEMAS
Nivel SEXTO PARALELO 02

2. MODELO MATEMATICO
El nuevo marco curricular establece, como meta prioritaria para el
sistema educativo, la alfabetización y el uso funcional de las
matemáticas por los escolares. La construcción de modelos
matemáticos y la resolución de problemas destacan como componentes
de la competencia básica en matemáticas, establecida para guiar el
aprendizaje de los escolares en esta materia durante su educación
obligatoria
¿Para qué sirve un modelo
matemático?
Para analizar la relación entre dos o
más variables, entender fenómenos
naturales, sociales, físicos, etc.
Existen muchos aspectos de la vida
cotidiana regidos por modelos
matemáticos. Lo que ocurre es que
no son modelos matemáticos
enfocados a teorizar. Al contrario,
son modelos matemáticos
formulados para que algo funcione.
Ejemplo, un coche.
Es una representación
simplificada, a través de
ecuaciones, funciones o
fórmulas matemáticas, de un
fenómeno o de la relación
entre dos o más variables.

3. . Parámetros: Se trata de valores conocidos o
controlables del modelo.
Restricciones: Límites que nos
indican que los resultados del análisis
son razonables.
Relaciones entre las variables: El
modelo establece una determinada
relación entre las variables
apoyándose en teorías económicas,
físicas, químicas
Representaciones simplificadas: Es
la representación de las relaciones
entre las variables estudiadas a través
de elementos de las matemáticas tales
como: funciones, ecuaciones,
fórmulas, etc.
ELEMENTOS BÁSICOS DE UN MODELO MATEMÁTICO
Referentes a su complejidad, todos ellos tienen un conjunto de características básicas:
Variables: Son los conceptos u objetos que se busca
entender o analizar. Sobre todo con respecto a su relación
con otras variables.
Ejemplo, salario de los trabajadores y lo que queremos
analizar son sus principales determinantes

4. CLASIFICACIÓN DE
MODELOS
MATEMÁTICOS
Según tipo de
representación
Cualitativos o conceptuales: Se refieren a un análisis de la
calidad o la tendencia de un fenómeno sin calcular un valor
exacto.
Cuantitativos o numérico: Los resultados obtenidos tienen un
valor concreto que tiene un cierto significado (puede ser exacto o
relativo).
Heurístico: Basado en posibles explicaciones sobre las causas de
los fenómenos observados.
Empírico: Utiliza la información de la experimentación real.
Según la
aleatoriedad
Determinista: No tiene incertidumbre, los valores son
conocidos.
Estocástico: No se conoce con exactitud el valor de las variables
en todo momento. Existe incertidumbre y por ende una
distribución de probabilidad de los resultados.
Según su aplicación u
objetivo
Simulación o descriptivo: Simula o describe un fenómeno. Los
resultados se enfocan a predecir qué sucederá una determinada
situación.
Optimización: Se utilizan para encontrar una solución óptima a
un problema.
De control: Para mantener el control de una organización
o sistema y determinar las variables que deben ajustarse
para obtener los resultados buscados.

5. PROCESO CONSTRUCCIÓN DE
MODELOS MATEMÁTICOS
Resultados
Decisiones
Situación
Administrativa
MODELO análisis
interpretación
intuición
abstracción
mundo simbólico
----------------------------------------------------------------------------------------------
-----------------
mundo real
La gráfica define el proceso de modelación a las dos
primeras etapas del proceso de toma de decisiones,
las cuales son: situación administrativa y decisiones

6. RESOLUCIÓN DE UN MODELO
MATEMÁTICO

7. MODELOS MATEMÁTICOS PARA RESOLVER PROBLEMAS REALES
 Por Dalia Patiño González. Puebla, Puebla. 14 de agosto de 2018 (Agencia Informativa Conacyt).- ¿Para qué sirven las
matemáticas cuando el cerebro o el corazón registran una actividad anómala; acaso pueden ayudar al neurólogo y al cardiólogo a
determinar el origen y tomar decisiones acertadas para revertirla? ¿Puede la matemática predecir la aparición de un brote viral y
proponer medidas para evitarlo? Las respuestas están en el trabajo que desarrolla el Centro Multidisciplinario de Modelación
Matemática y Computacional (Cemmac) de la Benemérita Universidad Autónoma de Puebla (BUAP).
 A tres años de su conformación, el Cemmac, integrado por un equipo multidisciplinario de investigadores de la BUAP, en su mayoría
matemáticos y físicos de la Facultad de Ciencias Físico Matemáticas (FCFM) y de otras unidades académicas como Electrónica y
Computación, en colaboración con especialistas de las áreas de Biología y Química, ha encaminado sus esfuerzos para demostrar que
las matemáticas son una ciencia útil que brinda soluciones efectivas a problemas prácticos y sobre todo vigentes.
 El doctor Andrés Fraguela Collar, coordinador del Cemmac, ha impulsado este modelo de aplicación matemática con la intención de
resolver dificultades reales, hacer visible la necesidad de este tipo de centros y formar perfiles que respondan a estos requerimientos
científicos.
 "Atacamos problemas en neurociencias, cardiología, geofísica y epidemiología, planteados por especialistas de estas áreas y eso
requiere entender de qué se está hablando porque a veces los resultados no se ajustan a la práctica y eso sucede porque, por lo general,
se hacen matemáticas alrededor de problemas reales, que es diferente a resolver problemas reales con matemáticas, y eso último es lo
que buscamos hacer, sin olvidar la importancia que tiene el desarrollo de esta ciencia en sí", declara para la Agencia Informativa
Conacyt el doctor Fraguela Collar.
 Conocimiento, aplicación y enseñanza
 El coordinador del Cemmac explicó que hoy en día las matemáticas juegan un triple papel en el contexto del conocimiento en general.
El primero está en su desarrollo como ciencia cuyo objeto de estudio es la abstracción. La segunda vertiente se refiere al uso que se les
da como instrumento para la solución de problemas prácticos, destacando la modelación matemática. Y lo último se refiere a la
importancia que tienen en la educación.
 "Es importante que se enseñen bien las matemáticas desde los niveles más básicos, pero eso no se puede lograr si los maestros no
están bien capacitados. Por eso se requieren programas para inducir en los maestros lo que llamamos pensamiento lógico matemático,
para que ellos lo puedan transmitir a los estudiantes. Por lo general, la enseñanza de las matemáticas en primaria, secundaria y
preparatoria se convierte en mecánica, memorística, en recordar fórmulas, y eso no permite desarrollar la abstracción y el
pensamiento lógico, que son componentes indispensables para crear individuos capaces de generar e innovar, sin lo cual es imposible
crear una sociedad basada en el conocimiento".