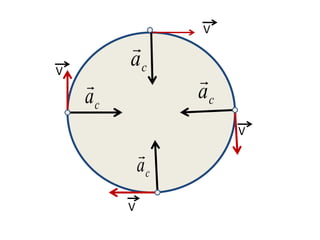
El documento describe el movimiento circular uniforme y variado. El movimiento circular uniforme ocurre cuando la velocidad es constante, mientras que el movimiento circular variado ocurre cuando la velocidad cambia con el tiempo. Se definen la aceleración centrípeta como la aceleración dirigida hacia el centro, y la aceleración tangencial como la derivada de la velocidad con respecto al tiempo.

1. OTRO MOVIMIENTO
BIDIMENSIONAL
MOVIMIENTO CIRCULAR

2. MOVIMIENTO CIRCULAR
UNIFORME
Ocurre cuando la rapidez es
constante es decir el
módulo de
la velocidad no cambia con
el tiempo

3. V
V R
V
V

4. Dis tan cia
Rapidez 
Tiempo

Rapidez  v
Dis tan cia de una vuelta  2R
Tiempo de una vuelta  P
 2R
v v
P

5. angulo de una vuelta
Rapidez angular 
tiempo de una vuelta
2

P
Por tan to :
v R
rapidez lineal  rapidez angular x radio

6. V

ac
V
 
ac ac
V

ac
V

7. ACELERACIÓN CENTRÍPETA
2
v
ac 
R
ac   R
2

8. MOVIMIENTO CIRCULAR VARIADO
Aparece cuando la rapidez varía con el tiempo.
Esto significa que hay otra aceleración que motiva
este cambio y se llama aceleración tangencial
Se define asi:
Aceleración tangencial=derivada de la magnitud
de la velocidad con respecto al tiempo

9. 
dv
at  o
dt
dv
at  donde hemos convenido
dt

que v  v

10. la aceleración total se escribe así :
  
aT  at  ac 
 v
at

ac 
aT
R

12. En un movimiento con aceleración tangencial constante
se pueden utilizar las siguientes fórmulas.
v cambio en la magnitud de la velocidad
at  
t int ervalo de tiempo
Si at  0, movimientouniformemente acelerado.
Si at  0, movimientouniformemente desacelerado.
Si at  0, movimientouniforme.

13. Rapidez en cualquier instante
v  v0  at t
Arco recorrido en el intervalo t
at 2
s  v0 t  t
2
Estas expresiones son válidas para el
giro en un solo sentido.

14. Ejemplo : La gráfica representa el movimiento de una partícula en un
instante dado.
Determinar: a)aceleración centrípeta, b)aceleración tangencial y c)rapidez

de la partícula para ese instante particular, si a  15.0m / s 2
T

v

at

30°
aT
 30° 
ac aT