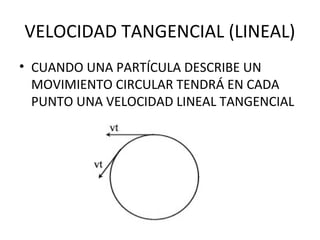
Este documento describe los conceptos fundamentales del movimiento circular, incluyendo el desplazamiento angular, la velocidad angular, la velocidad lineal tangencial, la aceleración angular y la aceleración centrípeta. Explica las relaciones entre estas cantidades y proporciona ejemplos numéricos de cómo calcularlas para diferentes situaciones de movimiento circular uniforme.

1. MOVIMIENTO CIRCULAR

2. MOVIMIENTO CIRCULAR
• EL MOVIMIENTO CIRCULAR ES TAMBIEN UN MOVIMIENTO EN
DOS DIMENSIONES Y POR LO TANTO PUEDE SER DESCRITO
EN FUNCIÓN DE SUS COMPONENTES RECTANGULARES COMO
EL MOVIMIENTO PARABÓLICO, SIN EMBARGO ES
CONVENIENTE DESCRIBIR EL MOVIMIENTO EN FUNCIÓN DE
SUS MAGNITUDES ANGULARES.
• A CONTINUACIÓN DEFINIREMOS LOS CONCEPTOS
RELACIONADOS CON EL TEMA .

3. DESPLAZAMIENTO ANGULAR ( θ )
• EL ÁNGULO EN QUE GIRA EL VECTOR DE
POSICIÓN DE UN OBJETO QUE SE MUEVE
CON UN MOVIMIENTO CIRCULAR

4. EL DESPLAZAMIENTO ANGULAR SE
PUEDE MEDIR EN:
• GRADOS SEXAGESIMALES : °
• REVOLUCIONES: REV
• RADIANES: RAD

5. DEFINICIÓN DE RADIAN
• SE DEFINE COMO EL ÁNGULO CENTRAL QUE
SUBTIENDE UN ARCO DE IGUAL LOGITUD QUE
EL RADIO DE LA CIRCUNFERENCIA
• 1RAD = 57.3°

6. VELOCIDAD ANGULAR ( ω )
• INDICA QUE TAN RÁPIDAMENTE GIRA EL VECTOR DE
POSICIÓN DE UN OBJETO QUE SE MUEVE CON
MOVIMIENTO CIRCULAR.
• VEL. ANGULAR MEDIA .- SE DEFINE COMO EL
COSIENTE ENTRE EL DESPLAZAMIENTO ANGULAR Y
EL TIEMPO EN QUE TARDA EL RECORRIDO
• ω = ∆θ/ ∆t , SI to = 0 Y θo = 0 ENTONCES QUEDA:
ω = θ/ t

7. UNIDADES DE VEL. ANGULAR (ω )
•RAD /SEG

8. MOVIMIENTO CIRCULAR
UNIFORME (MCU)
• LA VELOCIDAD ANGULAR MEDIA ES
CONSTANTE CUANDO RECORRE ÁNGULOS
IGUALES EN TIEMPOS IGUALES. EJEMPLO:

9. VELOCIDAD TANGENCIAL (LINEAL)
• CUANDO UNA PARTÍCULA DESCRIBE UN
MOVIMIENTO CIRCULAR TENDRÁ EN CADA
PUNTO UNA VELOCIDAD LINEAL TANGENCIAL

10. • CUANDO UN CUERPO DESCRIBE UNA
TRAYECTORIA CIRCULAR Y SU VELOCIDAD
TANGENCIAL CAMBIA SOLAMENTE EN
DIRECCIÓN SE DICE QUE DESCRIBE UN
MOVIMIENTO CIRCULAR UNIFORME (MCU)

11. EXISTE UNA RELACIÓN ENTRE LA VELOCIDAD
LINEAL Y LA VELOCIDAD ANGULAR
• Cuando una rueda gira, un punto en el borde
de la rueda recorre la longitud de arco s (en
metros, por ejm.). Esta longitud de arco está
en relación con el ángulo subtendido θ, por
definición de ángulo:
• θ = s /r
• s=θ r

12. RELACIÓN ENTRE LA VELOCIDAD LINEAL Y LA
VELOCIDAD ANGULAR
• 1) s = θ r.
• 2) ω = θ / t
• 3) v = s / t
• Se pueden combinar para encontrar una relación entre la
velocidad angular ω y la velocidad lineal v.
• Al sustituir 1 en 3 tenemos:
• v= θr pero θ/t = ω entonces finalmente queda:
t
v=ω r

13. ECUACIÓN DE VEL. LINEAL O
TANGENCIAL
•v = ω r
ESTA FÓRMULA SOLO ES VÁLIDA CUANDO
ω ESTE DADA EN RADIANES
• UNIDADES: m/s

14. FRECUENCIA Y PERIODO
• FRECUENCIA ( f ) .- ES EL NÚMERO DE
VUELTAS COMPLETAS O REVOLUCIONES QUE
EL OBJETO REALIZA POR UNIDAD TIEMPO.
• f = n/ t
• UNIDADES: rps , rpm,
• 1 HERTZ = 1 rps = seg-1

15. PERIODO ( P )
• ES EL TIEMPO EN QUE TARDA EN EFECTUAR
UNA VUELTA COMPLETA O REVOLUCIÓN.
• (INVERSO DE LA FRECUENCIA)
• P= t/n
• UNIDADES : SEGUNDOS

16. VELOCIDAD ANGULAR ( ω ) CUANDO
SE CONOCE LA FRECUENCIA
• SI UNA VUELTA COMPLETA EQUIVALE A 360°Y
ESO ES IGUAL A 2π RAD ENTONCES SE
SUSTITUYE EN LA ECUACIÓN DE ( ω )
• θ= 2πn rad = 360°
• ω = θ/ t ω = 2πn rad
t seg
• PERO n/t = f
• ω = 2πf UNIDADES rad/s

17. VELOCIDAD ANGULAR ( ω ) CUANDO
SE CONOCE EL PERIODO
• ω = 2π
P

18. PROBLEMAS
• UN DISCO DE 20CM DE DIÁMETRO GIRA CON
UN (MCU) A 150 RPM. CALCULAR:
• A)FRECUENCIA
• B)VELOCIDAD ANGULAR
• C)VEL. LINEAL A 5 CM DEL CENTRO DEL
DISCO
• D) VEL. LINEAL EN LA PERIFERIA DEL DISCO

19. ACELERACIÓN ANGULAR MEDIA( α )
• ES EL CAMBIO DE VELOCIDAD ANGULAR
DIVIDIDO ENTRE EL INTERVALO DE TIEMPO
QUE TARDA EN EFECTUARSE ESE CAMBIO.
• α = ωf - ωo
t
UNIDADES: RAD/SEG2

20. ACELERACIÓN CENTRÍPETA ( a )
La aceleración hacia el centro, que se necesita
para mantener un objeto moviéndose en un
círculo, se llama su aceleración centrípeta

21. PROBLEMAS
• UN OBJETO UNIDO AL EXTRMO DE UNA
CUERDA DE 60 CM DE LARGO GIRA 10
REVOLUCIONES EN 10 SEG CON RAPIDEZ
CONSTANTE , CALCULA:
• A) VEL. ANGULAR ( RAD /S)
• B) VEL. LINEAL DEL OBJETO
• C) ACELERACIÓN CENTRÍPETA.