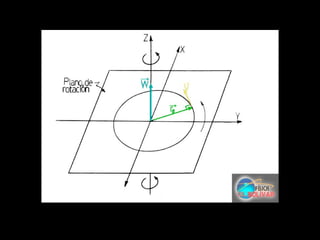
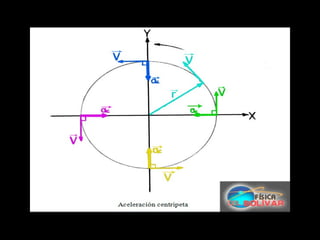
El documento describe los conceptos de movimiento circular uniforme y movimiento circular uniforme acelerado. Explica que en el movimiento circular uniforme, la velocidad angular es constante, mientras que en el movimiento circular uniforme acelerado, la velocidad angular cambia con el tiempo, dando como resultado una aceleración angular. También define las ecuaciones para el desplazamiento angular, la velocidad angular, la aceleración tangencial y la aceleración centrípeta en estos tipos de movimiento.

1. Movimiento circular uniforme acelerado !

2. El movimiento también se puede presentar en forma de giro o movimiento circular . Se realiza en un eje de giro, un radio constante y la trayectoria es una circunferencia. Como ejemplo de movimientos circulares encontramos: la rotación de la tierra sobre su eje , el carrusel de la feria, las aspas del ventilador ,entre otras .

3. Ejemplos

4. El movimiento circular uniforme se define como : el movimiento circular en el que un móvil se desplaza alrededor de un punto central siguiendo la trayectoria de una circunferencia , de tal modo que en tiempos iguales recorra espacios iguales .

5. Aceleración En la mayoría de los casos ,en el movimiento circular, después de un tiempo la velocidad angular puede variar ,dando como resultado una aceleración angular.

6. Para obtener las formulas del desplazamiento angular y la velocidad angular cuando el movimiento es circular uniforme acelerado , se combinan la velocidad angular media ω , y la aceleración angular α ,dando como resultado las siguientes ecuaciones . θ = ω 0 t+1/2 at² ω ² = ω ² 0 +2 α θ

7. Movimiento Lineal Movimiento Circular d = vt θ = ω t v = v 0 + at ω = ω 0 + α t = v 0 + v/2 = ω 0 + ω / 2 d = v 0 t + ½ at² θ = ω 0 t + ½ α t² v ² = v² 0 + 2 ad ω ² = ω ² 0 + 2 α θ

8. E j e m p l o ! ; )

9. Si las ruedas de un automóvil dan 40 vueltas en 3 segundos y tienen un diámetro de 64 cm ¿Con que velocidad se mueve el automóvil ? Datos θ = 40 vueltas D = 64 cm = 0.64m R = 0.32m V= ?

10. Fórmulas : ω = θ /t v = ω r Desarrollo: ω = θ /t = 40rev/ 3s =13.33rev/s(2 π rad/1rev)=83.73 rad/s V = ω r = (83.73 rad/s) (0.32m) = 26.8 m/s

11. Aceleración tangencial y centrípeta Aceleración tangencial (a t ) Esta aceleración se presenta cuando la velocidad tangencial de un cuerpo cambia , lo que da origen al movimiento circular no uniforme , esto se debe a que tanto l magnitud como la dirección de la velocidad tangencial cambian .

13. Debido a que la velocidad tangencial es variable ,la magnitud de la aceleración tangencial se puede calcular a patir de la aceleración angular ( α ),de la forma siguiente: a t = α r Otra forma de calcular la aceleracion tangencial es apartir de la segunda ley de newton : F t = ma t Donde: F t = magnitud de la fuerza tangencial neta (N) m = masa del cuerpo que gira (kg) a t = aceleración tangencial (m/s2 )

14. Aceleración centrípeta (a c ) A esta aceleración se le llama centrípeta (a c ) , que significa que se dirige hacia el centro . Se define como una cantidad vectorial que tiene magnitud así como dirección que apunta siempre hacia el centro de la circunferencia

15. La magnitud esta dada por : (a c ) = v² T / r = ω ² r Donde: v T = velocidad tangencial en el perímetro de la circunferencia (m/s) r= radio de la circunferencia (m) ω = velocidad angular (rad/s )

17. Fuerza centrípeta La segunda ley de newton establece que todo cuerpo que se encuentra acelerado debe tener una fuerza neta que actua sobre él (∑f=ma). Cuando el movimiento se realiza con velocidad constante,es decir ,circular uniforme ,la fuerza comunica al cuerpo una aceleración centripeta . ∑ f = ma c = m v² t / r = m ω ²

19. E j e m p l o ! ; )

20. Calcula la aceleración centrípeta de la tierra en su orbita alrededor del sol y la fuerza neta que éste ejerce sobre la tierra .supongamos que la órbita terrestre es un circulo de 1.50 x 10 11 m de radio . datos : r= 1.50 x 10 11 m a c = ? M t = 5.97 x 10 24 kg f c =?

21. Formulas a c = v² t /r = ω ² r f c = m a c desarrollo : Hagamos primero la onversion a rad/ seg la velocidad angular de la tierra y luego sustituyamosen las ecuaciones .

22. ω = 1 rev/365 dias (2 π rad/1 rev) (1 dia/86400s) = 1.99 x 10 –7 rad/s a c = ω ² r = (1.99 x 10 –7 rad/seg) 2 (1.50x10 11m) f c = m a c =(5.97x10 24 kg)(5.94x10 –3 m/s 2 )=3.55x10 22 N

23. Angélica García Córdoba Yuridia Gpe Salas Zamora Rubí Gpe Hernández cruz Dulce Thalía Hernández Acosta Beatriz Hernández Figueroa Mayela Odette Gutiérrez Gómez