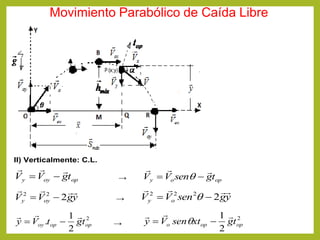
Este documento describe el movimiento circular y parabólico. Explica conceptos como velocidad angular, tangencial y aceleración angular y tangencial. Presenta fórmulas para calcular desplazamiento angular, período, frecuencia, altura y alcance máximo en movimiento parabólico. También cubre movimiento circular uniformemente variado y relaciones entre velocidad, aceleración angular y tangencial. Finalmente, incluye ejemplos numéricos para practicar los conceptos.

1. UNIVERSIDAD NACIONAL “HERMILIO VALDIZÁN”
FACULTAD DE CIENCIAS DE LA EDUCACIÓN
ESCUELA PROFESIONAL DE MATEMÁTICA Y FÍSICA
MECÁNICA DE SOLIDOS
CINEMÁTICA EN 2 Y 3 DIMENSIONES
Dr. Andrés A. Cámara Acero
Huánuco, Perú
2017

2. Movimiento Parabólico de Caída Libre
Es aquel movimiento compuesto por un movimiento horizontal,
considerado M.R.U. y un movimiento vertical, considerado caída libre
 = Ángulo de lanzamiento
Vo = Velocidad de lanzamiento
ga

 Raire = 0
g

= cte. 0º <  < 90º
oyV

= - yV

(en el punto R)
xV

= oxV

xV

= cte
oyV

= senVo

oxV

= cosoV

I) Horizontalmente: M.R.U.
oxx VV

 → cosox VV

 →
op
x
t
X
V



ttt VerticalHorizontal 

3. Movimiento Parabólico de Caída Libre
II) Verticalmente: C.L.
opoyy tgVV

 → opoy tgsenVV

 
ygVV oyy

222
 → ygsenVV oy

2222
 
2
2
1
. opopoy tgtVy

 →
2
2
1
opopo tgxtsenVy

 

4. III) Cálculo de la velocidad Instantánea en “P”
222
yxp VVV

 →
22
yxp VVV

 →
222
cos yop VVV

 
IV) Cálculo de la Dirección () de la Velocidad Instantánea o Tangencial
x
y
v
v


tan →


cos
tan
o
y
v
v


 → 








cos
arctan
o
y
v
v



5. V) Cálculo de Hmáx, máxx
_
y tvuelo
a) Hallamos la altura Máxima: Tramo OP
ygVV oyy

222
 → máxhy

 → 0yV

→ Máxoy hgV

20 2

 
g
senv
g
v
h ooy
Máx 


22
22

 →
g
senv
h o
Máx 

2
22


b) Hallamos el Tiempo de Vuelo
BROB tt  → BROBVuelo ttt  → OBV tt 2
voyy tgVV

 → voyoy tgVV

 → oyv Vtg

2
g
v
t
oy
v 

2
 →
g
senv
t o
v 

2

c) Alcance Horizontal ( x

)
opox tvx .

 → Máxsx

 → voxMáx tvs .

 →
g
senv
vs o
oMáx 

 

2
.cos
  cos.2
2
sen
g
v
s o
Máx 


 →
g
senv
s o
Máx 

 22


6. Ejemplo 01:
Desde una superficie horizontal se lanza una bala con una velocidad de 50
m/s y con un ángulo de 53º, halla:
a) La altura máxima, el tiempo de vuelo o permanencia en el aire y alcance
máximo.
b) El alcance y la altura en t= 3 segundos.
c) La velocidad instantánea y su dirección en t = 3 s. Considerar g = 10
m/s2

7. Características Físicas Del Movimiento
Circunferencial
Desplazamiento Angular ()
Desplazamiento Lineal(S)
Periodo (T)
Frecuencia (f)

8. Velocidad Angular Media (m)
0
0
0
tan tan :
lim
m
f
m
f
x
t
t t
Velocidad Angular Ins ea
d
t dt


 

 
 
 







  

Velocidad Tangencial (Vt)
0
: 0
tan tan
lim
T
T m
T
t
T
s
V
t
si t s
d
V V
t
En valor ins eo
s d
V
t dt
d s
V
dt



 



     
 


  



9. AceleraciónTangencial (at)
0
0
0
, var ,
tan tan :
lim
t
t
tf t
t
f
t t
t t
t
v
a La iaciónes unmódulo
t
V V
a
t t
EnValor Ins eo
V dv
a a
t dt 







  

0
0
2
2
tan tan :
lim
m
f o
m
f
t
t
t t
Envalor ins ea
t
d d
dt dt


 



 
 
 









 

10. VelocidadTangencial
Para “1” Vuelta
Para “m” Vueltas
( )
, ,t t
t
Vt V cte Enmódulo
S s
V cte S V xt t
t V
 
   
2
2 ,
2
t
t
S R
s R t T V
t T
R
V
T



    

2
2
2
S RxM
S RxM
t T Vt
t t
Vt Rf




   

Relación Entre Vt y 
2 ............(1)
2 ............(2)
(2) (1)
Vt fR
f
en
Vt xR

 





11. Movimiento Circular Uniformemente Variado
,
. . .
t
R
cte t cte
cte
M CU V
a cte
a cte


    
  
  
 
 
   
0 0 0 0
0
0 00
0
( 0)
t t
t t
t
d
d dt d dt
dt
t t t
t
 
 



    
       
  
    
       
 
   
 
 
 
0
2
0
0 000 0 0 0
2
0 00 0
0
2 2
0
0
( )
( )
2
0
0 ( )
2 2
1
2
t t t
t
tt t
d
d dt d t dt
dt
d t dt dt t dt
t
dt t dt t
t
t
t t
 

     
     
     
  
  
     
    
 
      
 
   
 
   
 
Para Determinar la  Tenemos que: t0 = 0
Para determinar : si  = 0 y t0 = 0

12.  0
0
0
2
00
2 2
2 20
0
2 2
0
0
....(1)
....(2)
(2) (1):
2
2
2 2
2
f
f
f
f
f
d
d
d
dt
d d
dt
dt
d d
en
d d
d d

  



  



 


  
 
 


     
 
   
  
  
 
  
  
 
   
 
    
 
 
También tenemos que:
Relación Entre Aceleración Tangencial ( ta ) y Aceleración Angular ( )
Sabemos que :
0 . 0.
0
tf t f R R
t
t
v v
a
t t
tf ta
v v
t
 

 
 
 
 
 
 
 
  
 
 
 
 


. .tR a R 

13. Aceleración del Movimiento Circular
UniformementeVariado (M.C.U.V)
 
2 2
2
2
2
2
: tan tan
:
:
: .
R N cp
R t
t R
N cp
N N
a Aceleraciónins ea
a a a
Aceleracion total
a a a
Enmódulo
a a a
v
a a R
R
R
como v R a a R
R


 
 
 
 
  
    

14. EJEMPLOS
5. Convierte 50 revoluciones a radianes
6. Convierte 48 π rad a revoluciones
7. Convierte 72 R.P.S. a rad/s
8. Convierte 1800 rev/min a rad/s
9. El ángulo girado por un esmeril está determinado por la siguiente
igualdad , determina:
a) La velocidad angular instantánea
b) La aceleración angular instantánea

15. EJEMPLOS
10.- Si en el problema anterior el tiempo transcurrido es de ½ minuto (30 segundos), determina:
a) El número de vueltas que ha dado en este tiempo
b) La  en este instante
c) La aceleración angular ()

16. EJEMPLOS
13.- La  de un volante disminuye de 450 rev/min a 400Rev/min en 2,5 segundos, encuentra:
a) La aceleración angular () a los 2,5 segundos
b) El número de revoluciones en ese tiempo
c) El tiempo necesario para que se detenga el volante

17. EJEMPLOS
14.- Una rueda de 50 cm de diámetro gira alrededor de un eje fijo con una
Re
4
v
o
s
  y tiene una
2
Re
6
v
s
  .
a) Determina la  que pasa luego de 3 segundos.
b) El ángulo que ha girado la rueda en ese intervalo
c) Qué velocidad tangencial posee en su borde cuando el tiempo es de 3 segundos
d) Cuál es su aceleración normal y tangencial, cuando el tiempo es de 3 segundos