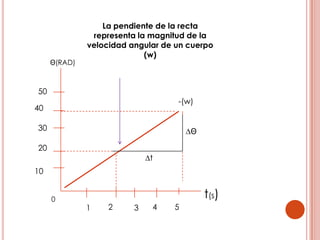
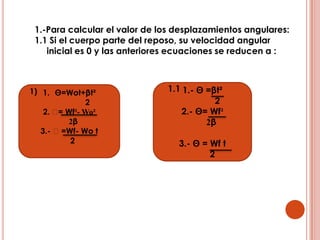
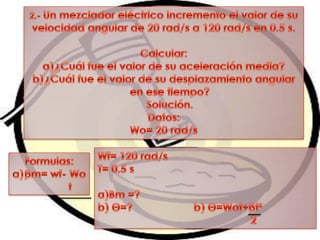
Un cuerpo en movimiento circular gira alrededor de un eje de rotación fijo. Este movimiento implica conceptos como desplazamiento, tiempo, velocidad y aceleración. Existen dos tipos de movimiento circular: uniforme, donde la velocidad no cambia aunque sí la dirección; y uniformemente acelerado, donde la velocidad angular cambia a una tasa constante.

3. Un cuerpo describe un movimiento circular
cuando gira alrededor de un punto fijo
central llamado Eje de rotación. Por
ejemplo, la rueda de la fortuna.
Para estudiar este movimiento es necesario
recordar los conceptos de :
Desplazamiento, Tiempo, Velocidad y
Aceleración.

4. El Movimiento
movimiento Uniformemente
Circular acelerado
uniforme

5. Es aquel en el que no existe cambio en la rapidez, sino solo
en la
dirección. a) La tensión hacia
dentro que el cordel
Ejemplo
:
ejerce sobre la piedra
hace que esta se
mueva en una trayectoria
circular
b) Si el cordel se rompe,
La piedra sale en
dirección
Tangente al circulo

6. ACELERACIÓN CENTRÍPETA

7. FUERZA CENTRÍPETA
Se define fuerza centrípeta como la fuerza
dirigida hacia el centro
que se requiere para mantener un
movimiento circular uniforme.

8. Donde m es la masa de un objeto que se mueve con
velocidad v a
Lo largo de una trayectoria circular de radio.
Las unidades que se utilicen para Fc , m, v y R deben
ser congruentes con el sistema de unidades elegido.

9. Angulo:
Es la abertura comprendida entre dos radios que limitan
un arco de circunferencia.
Radian:
Es el ángulo central que corresponde a un arco de longitud.
La equivalencia de un radian en grados sexagesimales se
determina sabiendo que :
I rad= 360°=180° = 57.3° = 57°18’
2п п

10. ANGULO Y VELOCIDAD ANGULAR
 El ángulo abarcado en un movimiento circular
es igual al cociente entre la longitud del arco
de circunferencia recorrida y el radio.
 La longitud del arco y el radio son magnitudes
de longitud, por lo que el desplazamiento
angular es el radian.
 La Velocidad angular es la variación del
desplazamiento angular por unidad de
tiempo:
 W= d1
dt

11. PERIODO Y FRECUENCIA
PERIODO
Es el tiempo que tarda un cuerpo en dar una vuelta
completa o en completar un circulo. Las unidades del
periodo son :
T= Segundos transcurridos
1 ciclo
FRECUENCIA
Es el numero de vueltas, revoluciones o ciclos que
efectúa un móvil en un segundo.
F= Numero de ciclos
1 Segundo

12. Velocidad Angular
La velocidad angular se representa:
W= 
t
Donde: W= Valor de la velocidad angular en rad/s
= Desplazamiento angular en rad.
T= tiempo que efectúa el desplazamiento en
segundos (s)
Entonces el valor de la velocidad angular se puede
expresar, respecto al desplazamiento y al cambio
de tiempo de esta forma :
W=∆= 2 -1
∆t t2-t1

13. También la podemos determinar si conocemos su
periodo (T). La expresión que utiliza es:
w= 2 rad = 2 en rad/s
T T
VELOCIDAD ANGULAR MEDIA
Cuando la velocidad angular de un cuerpo es
constante podemos determinar la magnitud de la
velocidad angular media al conocer la velocidad
angular inicial y su velocidad angular final:
Wm = Wf – Wo
2

14. MOVIMIENTO CIRCULAR UNIFORME (MCU)
Este movimiento se produce cuando un cuerpo con
velocidad angular constante describe ángulos iguales
en tiempos iguales. En un MCU se mantiene constante
su magnitud pero no su dirección ,toda vez que esta
siempre se conserva tangente a la trayectoria del
cuerpo.
La velocidad lineal o
tangencial representa la
velocidad que llevara un
cuerpo al salir disparado en
forma tangencial a la
circunferencia que describe.

15. Interpretación de las Graficas de desplazamiento angular-
tiempo y Velocidad angular-tiempo en el MCU.
En el movimiento circular uniforme de un cuerpo se obtuvieron los
datos contenidos en el cuadro
1.- Graficar los valores del desplazamiento angular en función del
tiempo, interpretar la pendiente y obtener el valor de dicha
pendiente.
2.- Graficar la magnitud angular del cuerpo en función del tiempo e
interpretar el significado físico del área.
 (rad)
Tiempo (s) Desplazamiento
50
angular =(rad)
0 0 40
1 9 30
2 18
20
3 27 10
4 36
5 45 t(s)
0 1 2 3 4 5

16. Solución
Calculo del valor de la pendiente recta:
a)Como se observa la pendiente de la recta representa la magnitud
de la velocidad angular.
w= ∆ = 36rad- 18rad
∆t 4s- 2s W=18rad = 9rad/s
2s
W(rad/s) b) Como la velocidad no cambia su magnitud
20
graficamos el mismo valor cada segundo
1O (RAD)
La pendiente de la recta
representa la magnitud de la
=wt t(s) velocidad angular de un cuerpo
1 2 3 4 5
(w)
50
-(w)
40
El área del rectángulo representa el 30 ∆
producto wt, el cual equivale al
valor desplazamiento angular. Por 20
∆t
lo tanto el valor de desplazamiento
será : 10
=wt= 9rad/s x 5s = 45 rad.
0 t(s)
1 2 3 4 5

17. Este movimiento se presenta cuando un móvil con trayectoria
circular tiene una aceleración angular que permanece
constante.
1 ( en lugar de d)
2 (w en lugar de v)
3.- (β en lugar de a ).
1.-Para calcular el valor de los desplazamientos angulares:
1.1 Si el cuerpo parte del reposo, su velocidad angular inicial es 0
y las anteriores ecuaciones se reducen a :
1.1 1.-  =βt²
1) 2
1. =Wot+βt² 2.- = Wf²
2 2β
2.  Wf²- Wo²
=
2β 3.-  = Wf t
3.- =Wf- Wo t 2
2

18. Velocidad Angular Instantánea
Representa el desplazamiento angular de un
cuerpo en un tiempo muy pequeño que casi tiende
a cero.
Winst = lim ∆
∆t 0 ∆t
Aceleración Angular Media
Cuando durante el movimiento circular de un
cuerpo su velocidad angular no permanece
constante, si no que sufre una aceleración angular
Βm = wt - w0 =∆w
tf - t0 ∆t

19. Donde
Βm = Valor de la aceleración angular media en rad/s²
Wf =Magnitud de la velocidad angular final en rad/s
W0= Magnitud de la velocidad angular inicial en rad/s
∆t= Tiempo durante el cual varia la velocidad en
segundos (s)
ACELERACION ANGULAR INSTANTANEA
Cuando el movimiento acelerado de un cuerpo que
sigue una trayectoria circular y el intervalo de tiempo es
tan pequeño que tiende a cero, la aceleración angular
del cuerpo será la instantánea.
β Inst. = lim ∆w
∆t 0 ∆t

20. PROBLEMAS
1.- Un engrane adquirió una velocidad angular cuyo
valor es de 2512 rad/s en 1.5 s ¿Cuál fue su
aceleración angular?
DATOS: Formula:
Wf= 2512 rad/s Β=w
T= 1.5 s t
Β=?
Sustitución y resultado:
Β= 2512 rad/s = 1674.66 rad/s²
1.5 s

22. Finalmente después de haber llevado
acabo este trabajo y solucionar
problemas respecto al movimiento
circular podemos decir que esta clase
de movimiento lo aplicamos en la
vida cotidiana haciendo uso de las
variadas formulas que aquí hemos
presentado.