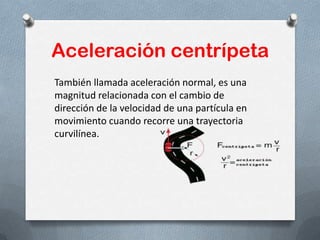
Este documento describe el movimiento circular uniforme. Define este movimiento como cuando un cuerpo se mueve a lo largo de una circunferencia a una velocidad constante. Explica conceptos como periodo, frecuencia, velocidad angular, velocidad lineal y aceleración centrípeta. También incluye ejemplos y fórmulas para calcular estas cantidades.

1. MOVIMIENTO
CIRCULAR
UNIFORME
DAVID PAREDES BRAVO

2. DEFINICIÓN
O Un cuerpo posee un movimiento circular
uniforme, cuando se mueve sobre una
circunferencia con rapidez constante.
O El movimiento circular está presente en
multitud de artilugios que giran a nuestro
alrededor: los motores, las manecillas de
los relojes y las ruedas son algunos
ejemplos que lo demuestran.

3. CARACTERÍSTICAS
Entre las características más visibles que tiene el MCU, podemos
mencionar las siguientes:
• Todos los cuerpos describen una trayectoria
circular, recorriendo arcos iguales en tiempos iguales.
• En todos, existe un eje de rotación real o imaginario.
• Se mueven con dos tipos de velocidades: una lineal o
tangencial (VL) y otra angular (W).
• La velocidad lineal (VL) es siempre tangente a la curva y
constante en magnitud, pero cambia permanentemente de
dirección y sentido.
• La velocidad angular (W), es constante en todo el
movimiento.
• La aceleración del movimiento es centrípeta, es decir que
siempre va dirigida al centro de la circunferencia.
• El vector velocidad y el vector aceleración son
perpendiculares en cualquier punto de la trayectoria.

4. PERIÓDO Y FRECUENCIA
O Dos conceptos importantes de movimiento
circular son el periodo y la frecuencia. El
periodo[p] es le tiempo que tarda un cuerpo en dar
una vuelta completa. Sus unidades son los
segundos(s). Por ejemplo, el periodo de rotación y
traslación de la tierra es de 24 hora s y 365 días
respectivamente.
La frecuencia[f] se define como el numero de
vueltas completas que efectúa un cuerpo en una
unidad de tiempo. Sus unidades son Hertz(Hz).
Cuando un cuerpo presenta una frecuencia de
1Hz, significa que realiza una vuelta completa
(1ciclo=2πrad) en un segundo.

5. Desplazamiento angular y
radian
El desplazamiento angular de un cuerpo describe la
cantidad de rotación. Se representa por el ángulo
formado al girar el cuerpo del punto A al B.
Por su parte, el radian (rad) es una magnitud
geométrica, un numero sin unidades, es el cociente
entre dos longitudes, el arco (s) y el radio (r). θ = s/r
La relación entre radianes y grados se obtiene
considerando que una vuelta completa es igual a
360º .

6. Velocidad Angular
Se denomina rapidez angular media al cociente
entre el ángulo barrido, es decir θ y el tiempo.
En el instante t' el móvil se encontrará en la
posición P' dada por el ángulo θ'. El móvil se
habrá desplazado θ = θ' - θ en el intervalo de
tiempo t = t‘ - t comprendido entre t y t'.

7. Aceleración angular
Se denomina aceleración angular media al cociente
entre el cambio de velocidad angular y el intervalo
de tiempo que tarda en efectuar dicho cambio.
Si en el instante t la velocidad angular del móvil
es ω y en el instante t' la velocidad angular del
móvil es ω‘, la velocidad angular del móvil ha
cambiado ω = ω‘ - ω en el intervalo de
tiempo t = t'- t comprendido entre t y t‘.

8. Velocidad lineal o tangencial
El vector velocidad lineal es tangente a la trayectoria
circular, por ello también se le denomina velocidad
tangencial.
La velocidad tangencial es la velocidad del móvil
(desplazamiento del móvil en el tiempo). Por lo tanto
para distintos radios y a la misma velocidad angular,
el móvil se desplaza a distintas velocidades
tangenciales.

9. Aceleración centrípeta
También llamada aceleración normal, es una
magnitud relacionada con el cambio de
dirección de la velocidad de una partícula en
movimiento cuando recorre una trayectoria
curvilínea.

10. Fuerza centrípeta
Ahora, según la segunda ley de Newton, la variación de
velocidad en un cuerpo es producida por una
fuerza, por lo que la aceleración centrípeta se debe a la
acción de una fuerza, llamada Fuerza centrípeta.
Dicha fuerza es un vector dirigido hacia el centro de la
circunferencia.
Como el módulo de una fuerza es masa por
aceleración, tendremos que:
Fc = m • ac
Pero sabemos que ac = v2/r, por lo que el módulo de
Fc será:

11. FÓRMULAS

12. FÓRMULAS

13. EJERCICIOS
O un objeto lleva un Movimiento circular de 6cm de radio girando a 200 revoluciones por minuto.
Calcular el periodo, la frecuancia, el angulo descrito en 20 segundos y la aceleracion normal
DATOS
Radio de la trayectoria ........ R = 6 cm
frecuencia de giro ................ f = 200 RPM
a) Vamos a convertir la frecuencia de revoluciones por minuto a revoluciones por segundo ó
Hertz
........... rev..... 1 min... 10
f = 200 ------- x --------- = --- rev /s ó Hertz
........... min.. .. 60 s .... 3
b) El Período (T) es la inversa de la frecuencia
...... 1........1....... 3
T = --- = -------- = ---- = 0,3 s
.......f .... 10/3.....10
c) La velocidad angular del objeto ( ω ) será :
................ ω = 2 . π . f
reemplazando valores :
................ ω = 2 . π ( 10 /3 )
............ ..........20 π
................ ω = ------- rad /s
............. ...........3

14. EJERCICIOS
O - Un ventilador gira con una
velocidad angular constante de 20
revoluciones por segundo. Calcular:
A- velocidad lineal si el radio de la
circunferencia es 15cm
B- la longitud del arco recorrido en
4 horas en funcionamiento

15. EJERCICIOS
O a) La frecuencia de rotación del ventilador es...... f = 20 rev /s
b) Con este dato, hallamos su velocidad angular ( ω )
................ ω = 2 . π . f
reemplazando valores :
ω = 2 . π ( 20 )
ω = 40 π rad /s
c) La velocidad lineal ( V ) , con R = 15 cm será :
................ V = ω . R
reemplazando valores ;
................ V = ( 40 π ) ( 15 )
................ V = 1884,96 cm /s
................ V = 18,85 m /s

16. EJERCICIOS
Ouna rueda gira a razon de
800 radianes por minuto.
Calcular la velocudad lineal
de un punto situado a 6cm
del eje y su aceleracion
centripeta.

17. EJERCICIOS
O velocidad angular ( ω ) = 800 rad /min
...... rad..... 1 min.... 40
800 -------- x -------- = ---- rad /s
...... min...... 60s.......3
a) La velocidad lineal ( V ) de un punto situado a 6 cm de su eje
será :
................ V = ω . R
reemplazando valores :
................ .......( 40 )
.......... ...... V = -------- ( 6 )
................. .........3
................ V = 80 cm /s .............. ........ ............. RESPUESTA
b) La aceleración centrípeta la encontramos aplicando :
................ ac = ω*2 . R
reemplazando valores :
.......... .......... 40
................ ac = ( ----- )*2 ( 6 )
................. ..........3
................ ac = 1066,66 cm /s2

18. EJERCICIOS
O un móvil recorre una circunferencia
de 5cm de radio con una velocidad
angular de 10 revoluciones por
minuto. Calcular
periodo, frecuencia, velocidad lineal
y aceleración normal.

19. EJERCICIOS
O ) La frecuencia de giro del móvil es 10 RPM. vamos a convertirla a revoluciones por
segundo -o Hertz :
......... rev .... 1 min...... 1
f = 10 ------- x ---------- = ---- rev /s ó Hertz ..... ...... RESPUESTA
......... min ..... 60 s ......6
b) El Período ( T ) es la inversa de la frecuencia .......
......1....... 1
T = ---- = ------- = 6 segundos ....... ................... ... RESPUESTA
.......f .....1 /6
c) La velocidad angular ( ω ) del móvil será :
................ ω = 2 . π . f
reemplazando valores :
................ ω = 2 . π ( 1 /6 )
.................. ......π
................ ω = ----- rad /s
.................. ......3
d) La velocidad lineal ( V ) será :
................ V = ω . R
reemplazando valores :
................. .........π
................ V = ( ----- ) ( 5 )