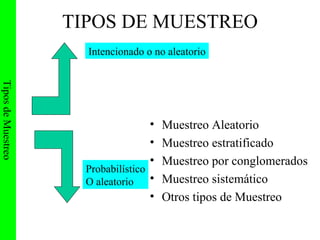
Este documento introduce conceptos básicos sobre muestreo estadístico, incluyendo los tipos de muestreo como aleatorio, estratificado y por conglomerados. También discute la inferencia estadística a partir de muestras, la distribución de estimadores y la estimación por intervalos de confianza.

1. MUESTREO INTRODUCCIÓN. PRIMEROS CONCEPTOS TIPOS DE MUESTREO INFERENCIA ESTADÍSTICA DISTRIBUCIÓN EN EL MUESTREO DE UN ESTADÍSTICO O ESTIMADOR ESTIMACIÓN PUNTUAL ESTIMACIÓN POR INTERVALOS. INTERVALOS DE CONFIANZA

2. INTRODUCCIÓN Deseamos conocer la estatura de un regimiento de 942 soldados. ¿Cómo lo hacemos? Deseamos conocer la estatura de todos los hombres españoles de edad comprendida entre loa 18 y 35 años. ¿Cómo lo hacemos? Deseamos conocer la vida media de una marca de bombillas. ¿Cómo lo hacemos? NECESITAMOS EL MUESTREO Introducción. Primeros conceptos Deseamos conocer la intención de voto de una población

3. PROS Y CONTRAS EN EL MUESTREO Proceso más económico Proceso más rápido El estudio puede suponer la destrucción de los objetos estudiados ¿Representatividad de la población?. ¿Cómo hacer inferencia a la población? ¿Qué confianza nos merecen los datos?. Fiabilidad Introducción. Primeros conceptos ¡¡DAR UNA RESPUESTA!!

4. A LA HORA DE ELEGIR UNA MUESTRA ESPECIFICAR: Método de selección. Tipo de muestreo El tamaño de la muestra Grado de fiabilidad (Estimación del error en términos de probabilidad) Error o sesgo de selección Error o sesgo de no respuesta Introducción. Primeros conceptos

5. TIPOS DE MUESTREO SESGO: FACTOR DE ELEVACIÓN: FRACCIÓN DE MUESTREO: Tipos de Muestreo Error que se comete al muestrear, puede ser debido a que la muestra no ha sido al azar o a otras causas, como la no respuesta Tamaño Poblacional/Tamaño muestral Tamaño muestral/Tamaño poblacional Algunos conceptos previos:

6. TIPOS DE MUESTREO Muestreo Aleatorio Muestreo estratificado Muestreo por conglomerados Muestreo sistemático Otros tipos de Muestreo Tipos de Muestreo Intencionado o no aleatorio Probabilístico O aleatorio Intención de voto Medios de comunicación en ciertos programas Encuesta a la entrada de un cine

7. MUESTREO ALEATORIO Tipos de Muestreo SIN REEMPLAZAMIENTO CON REEMPLAZAMIENTO (Muestreo Aleatorio Simple) En una ciudad se quiere hacer un estudio para conocer qué tipo de actividades se realizan en el tiempo libre. Se desea estudiar la población total de ballenas en elmundo

8. MUESTREO ESTRATIFICADO Tipos de Muestreo Regalo a la directora del IES de zapatillas deportivas para los alumnos Población Total = N Creamos k estratos heterogéneos entre sí con tamaños: Sin elementos comunes en cada estrato Proporcional al tamaño del estrato ¿Cómo elegir el tamaño de las muestras de cada estrato para que el total sea n? Igual en cada estrato

9. MUESTREO POR CONGLOMERADOS Tipos de Muestreo Gastos familiares de una sociedad Población se divide en grupos en los cuales se haya representada la misma.Los grupos son homogéneos entre sí, pero heterogéneos sus individuos Controlar el nivel de audiencia de un canal televisivo Estudio del efecto de fiebre Actosa en la cañada bovina de Andalucía

10. MUESTREO SISTEMÁTICO Tipos de Muestreo Tamaño poblacional = N Tamaño muestral = n Supongamos los elementos ordenados y numerados del 1 hasta N, se elige el primer elemento al azar y los n-1 restantes de k en k a partir del primero. Eliges al azar el elemento a {1,2,.....,N/n} Los siguientes: a + k , a+2k,a+3k,......a+(n-1)k

11. SACAR UN NÚMERO ALEATORIO CON LA CALCULADORA Tipos de Muestreo Supongamos que queremos sacar un´número aleatorio entre a y b ambos incluidos: {a, a+1, a+2,.........................,b} [0,1) .(b+1-a) [a,b+1) [0,b-a+1) +a [a,b+1) E([a,b+1))

12. INFERENCIA ESTADÍSTICA Inferencia Estadística POBLACIÓN QUEREMOS CONOCERLA ¿Qué queremos conocer? ¿Cómo? MUESTRAS Media Poblacional Desv. Típica Tamaño Población Proporción ESTIMADORES O ESTADÍSTICOS

13. EJEMPLOS Inferencia Estadística Queremos saber el tiempo medio de vida una marca de bombillas Queremos saber el peso medio de los tomates de una huerta Queremos saber el número de ballenas existentes en los océanos Queremos saber la proporción votantes de un determinado partido político

14. PROCEDIMIENTOS DE INFERENCIA Inferencia Estadística Procedimientos Según objetivo de estudio Según tipo de información que utiliza Métodos Paramétricos Métodos No Paramétricos Infer. Clásica Inf. Bayesiana ¿Cómo Llevarla a cabo? Estimación Contraste Hipótesis Puntual Por Intervalos

15. DISTRIBUCIÓN DE LOS ESTIMADORES Distribución de los estimadores. ¿Cómo saber la cantidad de cada color? ¿Cómo hacer más fiable nuestra inferencia? ¿Cuál de los dos resultados es más fiable? ¿Con cuál nos quedamos? EJEMPLO1: COMPOSICIÓN DE UNA BOLSA. DISTRIBUCIÓN DE PROPORCIONES

16. DISTRIBUCIÓN DE LOS ESTIMADORES Distribución de los estimadores. EJEMPLO2: DISTRIBUCIÓN DE MEDIAS 1 3 5  =3  =1,63 ¿Qué forma tiene? ¿Media? ¿Desv. Típica? ¿Cómo saber la MEDIA y la DESV. TÍPICA de la población? (1,1) 1 9 8 7 6 5 4 3 2 Nº MUESTRA (5,5) (5,3) (5,1) (3,5) (3,3) (3,1) (1,5) (1,3) MEDIAS MUESTRAS

17. DISTRIBUCIÓN DE LOS ESTIMADORES Distribución de los estimadores. Supongamos que tenemos una V.A de una población de la que queremos conocer un parámetro : X (  ,  2 , p) ¿Cuál será su distribución? Sean: X1: V.A en la muestra 1 X2: V.A en la muestra 2 ..................................... Xi: V.A en la muestra i P1 P2 ... Pi P TEOREMA CENTRAL DEL LÍMITE

18. DISTRIBUCIÓN MUESTRAL DE MEDIAS Distribución de los estimadores. X1: V.A en la muestra 1 X2: V.A en la muestra 2 ..................................... Xi: V.A en la muestra i a) Independientemente de N y del tipo de muestreo b) Si N finita (n<=30) y muestreo sin reemplazamiento: ; s Si N infinita (n>30) o muestreo con reemplazamiento: TEOREMA CENTRAL DEL LÍMITE

19. ESTIMADORES PUNTUALES Distribución de los estimadores. PROPIEDADES DESEABLES DE LOS ESTIMADORES Centrado o Insesgado Consistente Eficiente Suficiente De la media poblacional: Media muestral De la proporción poblacional: Proporción en la muestra De la varianza poblacional Cuasivarianza muestral SIMULACIÓN

20. ESTIMACIÓN POR INTERVALOS. INTERVALOS DE CONFIANZA Intervalos de confianza. Ejemplo: Distancia de los alumnos al centro INTERVALO DE CONFIANZA Se llama así a un intervalo en el que sabemos que está un parámetro, con un nivel de confianza específico DEFINICIONES NIVEL DE CONFIANZA Probabilidad de que el parámetro a estimar se encuentre en el intervalo de confianza. Nc=1-  ERROR DE ESTIMACIÓN Es el error que máximo que admitimos a un nivel de confianza específico, es por lo tanto el radio del intervalo:

21. ESTIMACIÓN POR INTERVALOS. INTERVALOS DE CONFIANZA Intervalos de confianza. -k k

22. RELACIONES ENTRE EL ERROR, EL TAMAÑO MUESTRAL Y EL INTERVALO DE CONFIANZA Intervalos de confianza. -k k SIMULACIÓN

23. ¿QUÉ PROBLEMAS SE NOS PUEDEN PRESENTAR? Intervalos de confianza. CALCULAR EL INTERVALO DE CONFIANZA dado el tamaño muestral y el nivel de confianza CALCULAR EL TAMAÑO MUESTRAL PARA ASEGURAR QUE CON UNA CIERTA CONFIANZA LA MEDIA POBLACIONAL SE ENCUENTRA EN UN INTERVALO CALCULAR EL ERROR QUE SE COMETE AL ESTIMAR POR INTERVALOS SIMULACIÓN

24. FIN