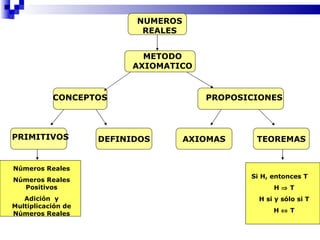
El documento habla sobre los números reales, incluyendo las propiedades básicas de la suma, resta, multiplicación y división. También define conceptos como intervalos, ecuaciones, desigualdades y conjuntos de números como naturales, enteros, racionales e irracionales. Finalmente, explica las operaciones básicas en el conjunto de los números reales y los axiomas y propiedades que las rigen.

1. NUMEROS REALES. VALOR ABSOLUTO. DESIGUALDADES UNIDAD I: PRIMERA PARTE.

2. TEMA I 1.- Los Números Reales . 1.1.- Suma y Multiplicación de Números Reales. Propiedades básicas de la Suma y la Multiplicación. Definición de Diferencia y Cociente. Algunas propiedades de los Números Reales. Axioma de Orden. Definición de desigualdades . Intervalos. Tipos de Intervalos.

3. Ecuaciones: Dos expresiones algebraicas unidas por el signo igual. Ejemplo: 2x + 1 = 3x – 2 ,

4. Nota: Resolver una ecuación o una inecuación significa hallar el conjunto solución de la igualdad o desigualdad respectivamente. El conjunto solución, es el conjunto formado por todos los números reales que son solución de la ecuación o inecuación. El conjunto solución de una ecuación es finito, mientras que el conjunto solución de una inecuación, en general, es infinito.

5. Ejemplos: 1.- Resolver la siguiente ecuación: x – (6 – 2x) = 8(x – 2) 2.- Resolver la siguiente inecuación: x – (6 – 2x) > 8(x – 2)

6. DEFINIDOS AXIOMAS TEOREMAS NUMEROS REALES METODO AXIOMATICO CONCEPTOS PROPOSICIONES PRIMITIVOS Números Reales Números Reales Positivos Adición y Multiplicación de Números Reales Si H, entonces T H  T H si y sólo si T H  T

7. Conjuntos de Números: Naturales: 1,2,3,4,... Denotado por: Enteros: ..., -3,-2,-1,0,1,... Denotado por: Racionales: Números que pueden escribirse de la forma: m/n donde n es distinto de 0 Se denota por: Números Reales

8. Ejemplos

9. En general: “ Un número es racional si es entero o, si su fracción decimal es finita o infinita periódica” 2; 3; 176543; 34,456; -456,456456456... En otro caso es irracional: Estos y otros forman el conjunto de los irracionales denotado por

10. Asi tenemos: e N Z Q R

11. El Conjunto de los Números Reales R Está formado por todos los números, racionales e irracionales que pueden medir longitudes, incluyendo sus negativos y el cero.

12. La Recta real La recta real es una representacion geométrica del conjunto de los números reales . Tiene su origen en el cero , y se extiende en ambas direcciones, los positivos en un sentido (normalmente hacia la derecha) y los negativos en el otro (normalmente a la izquierda). Existe una correspondencia uno a uno entre cada punto de la recta y un número real. Obtenido de " http://es.wikipedia.org/wiki/Recta_real "

13. Números Reales, Racionales e Irracionales Recta Real Números Racionales Pueden expresarse como cociente de dos enteros Números Irracionales No pueden expresarse como decimales finitos ni periódicos Decimales finitos Periódicos 1 3 =0,333...=0,3 0 1 2 3 4 2 e   2  1,414213562   3,141592654 e  2,718281828 2 5 =0,4

14. Operaciones en R Suma o adición: Multiplicación:

15. Axiomas de la Suma y Multiplicación Leyes conmutativas: Leyes Asociativas: Ley Distributiva: Elementos Identidad: Inversos: Aditivo: Multiplicativo:

16. Sustracción y división Para definir estas operaciones hacemos uso de las propiedades anteriores, de manera que: