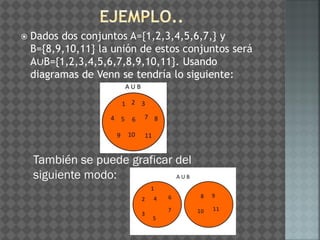
El documento define conceptos matemáticos como conjuntos, uniones de conjuntos, números naturales, desigualdades, valor absoluto y desigualdades de valor absoluto. Explica que un conjunto es una colección de objetos y que la unión de conjuntos une los elementos de varios conjuntos sin repetirlos. También define números naturales como los usados para contar y explica conceptos como el número cardinal y ordinal. Luego, introduce desigualdades, el valor absoluto y cómo resolver desigualdades de valor absoluto.

1. Estudiante:
Rubí Prieto
Nro. Cedula:
30.395.948
Sección:
0101.
Materia:
Matemática.

2. Se denomina conjunto a toda unión de objetos,
dichos objetos se denominan elementos del
conjunto. Los conjuntos se denotan con letras
mayúsculas y se colocan entrellaves.
Ejemplos:
 1) A={1,2,3,4,5}
 2) B={a,e,i,o,u}
 3)C={1,2,3,4,…}
 4)D={lunar,mar,…,dom}

3.  Unión o reunión de conjuntos.
 Es la operación que nos permite unir dos o más
conjuntos para formar otro conjunto que contendrá
a todos los elementos que queremos unir pero sin
que se repitan. Es decir dado un conjunto A y un
conjunto B, la unión de los conjuntos A y B será otro
conjunto formado por todos los elementos de A, con
todos los elementos de B sin repetir ningún
elemento. El símbolo que se usa para indicar la
operación de unión es el siguiente: ∪. Cuando
usamos diagramas de Venn, para representar la
unió de conjuntos, se sombrean los conjuntos que
se unen o se forma uno nuevo. Luego se escribe por
fuera la operación de unión.

4.  Dados dos conjuntos A={1,2,3,4,5,6,7,} y
B={8,9,10,11} la unión de estos conjuntos será
A∪B={1,2,3,4,5,6,7,8,9,10,11}. Usando
diagramas de Venn se tendría lo siguiente:
También se puede graficar del
siguiente modo:

5. Un número natural es cualquier número que se usa
para contar un grupo de cosas. Debido a que los
números naturales se suelen usar para contar
un grupo de cosas, se usa el 0 para indicar la
ausencia de los mismos, los números naturales se
representa de la siguiente manera:
= { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ... }
Los tres puntos suspensivos indican hasta el infinito.
El símbolo , se usa para representar a los números
Naturales, Las llaves {} encierran a los números que
son todos naturales hasta el infinito. Los números
naturales son infinitos, y lo infinito significa que estos
números no tienen fin.
También se suele representar los números naturales
usando la siguiente notación similar a la anterior.
= { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ..., ∞ }

6. Pero en este caso los puntos suspensivos, indican
que existen números después del once hasta el
infinito, y el símbolo ∞ se usa para representar lo
infinito.
Cuando usamos los números naturales para contar
un grupo de cosas, y el número que obtenemos al
contar la última cosa, recibe el nombre de número
cardinal. Por ejemplo el número cardinal de las
letras de la palabra LIBERTAD es 8, es decir la
cantidad de letras que tiene la palabra LIBERTAD.
Cuando contamos cualquier grupo de cosas, el
número natural que corresponde a cada cosa o
elemento del grupo de cosas que se cuenta, se
llama número ordinal de dicha cosa. El número
ordinal representa a un elemento de un grupo de
cosas, teniendo en cuenta el orden de los mismos.

7.  Una desigualdad es equivalente a la desigualdad
del mismo sentido obtenida sumando una misma
cantidad a sus dos miembros. Una desigualdad es
equivalente a la desigualdad del mismo sentido
obtenida multiplicando sus dos miembros por una
misma cantidad positiva. Una desigualdad es
equivalente a la desigualdad de sentido opuesto
obtenida multiplicando sus dos miembros por una
misma cantidad negativa. El producto de dos
cantidades es positivo si, y sólo si, las dos
cantidades son positivas o las dos son negativas.
decir que dos desigualdades son equivalentes
significa que las dos son ciertas o ninguna es
cierta y que ambas se satisfacen para los mismos
valores de las variables.

8.  El valor absoluto es un concepto que está presente en diversos
contextos de la Física y las Matemáticas, por ejemplo en las
nociones de magnitud, distancia, y norma. En casos más
complejos es un concepto muy útil, como en las definiciones
de cuaterniones, anillos ordenados, cuerpos o espacios
vectoriales.
 El valor absoluto o módulo de un número real cualquiera es el
mismo número pero con signo positivo. En otras palabras, es el
valor numérico sin tener en cuenta su signo, ya sea positivo o
negativo. Por ejemplo, el valor absoluto del número −4−4 se
representa como |−4||−4| y equivale a 44, y el valor absoluto
de 44 se representa como |4||4|, lo cual también equivale
a 44.
 En la recta numérica se representa como valor absoluto a
la distancia que existe de un punto al origen. Por ejemplo, si se
recorren 4 unidades del cero hacia la izquierda o hacia la
derecha, llegamos a −4−4 o a 44, respectivamente; el valor
absoluto de cualquiera de dichos valores es 44.

9. Formalmente, el valor absoluto de todo
número real está definido por:
|a|={a,−a,sisia≥0a<0|a|={a,sia≥0−a,sia<0
Como podemos notar, el valor absoluto de un
número real es siempre mayor que o igual a
cero y nunca es negativo. Además, el valor
absoluto no sólo describe la distancia de un
punto al origen; de manera general, el valor
absoluto puede indicar la distancia entre dos
puntos cualesquiera de la recta numérica. De
hecho, el concepto de función
distancia o métrica en Matemáticas surge de
la generalización del valor absoluto de la
diferencia

10. Una desigualdad de valor absoluto es una desigualdad que tiene un
signo de valor absoluto con una variable dentro. Desigualdades de
valor absoluto (<):
La desigualdad | x | < 4 significa que la distancia entre x y 0 es menor
que 4.
Así, x > -4 Y x < 4. El conjunto solución es .
Cuando se resuelven desigualdes de valor absoluto, hay dos casos
a considerar.
Caso 1: La expresión dentro de los símbolos de valor absoluto es
positiva.
Caso 2: La expresión dentro de los símbolos de valor absoluto es
negativa.
La solución es la intersección de las soluciones de estos dos
casos.
En otras palabras, para cualesquiera numéros reales a y b , si | a |
< b , entonces a < b Y a > - b .

11.  https://www.varsitytutors.com/hotmath/hot
math_help/spanish/topics/absolute-value-
inequalities#:~:text=Una%20desigualdad%20d
e%20valor%20absoluto,absoluto%20con%20un
a%20variable%20dentro.
 https://es.scribd.com/document/480905894
/Numeros-Reales#from_embed
 https://www.superprof.es/apuntes/escolar/
matematicas/algebra/inecuaciones/ejercicio
s-de-inecuaciones.html