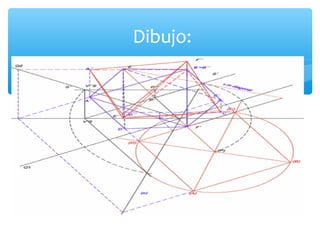
El documento describe las propiedades de un octaedro, incluyendo que es un poliedro regular con 8 triángulos equiláteros iguales. Explica que tiene 6 vértices, 12 aristas y 8 caras, y presenta fórmulas para calcular su área y volumen. También discute su simetría octaédrica.

1. Año de la Intengracion Nacional y el
Reconocimiento de Nuestra Diversidad

Institución Educativa: Ofelia Velasquez.

Alumna: Claudia Paola Cardenas Ramirez.

Profesora: Jane Rodriguez Sanchez.

Grado: 5

Sección: “B”

Tema: Octaedros.
TARAPOTO__ PERU.

2. OCTAEDRO
Octaedro es un poliedro de ocho caras. Con este número de caras puede ser un
poliedro convexo o un poliedro un poliedro de ocho caras. Con este número de
caras puede ser un poliedro convexo o un poliedro cóncavo. Sus caras han de ser
polígonos de siete lados o menos. Si las ocho caras del octaedro son triángulos
equiláteros, iguales entre sí, el octaedro es convexo y se denomina regular, siendo
una figura de los llamados sólidos platónicos.s han de ser polígonos de siete lados
o menos. Si las ocho caras del octaedro son triángulos equiláteros, iguales entre
sí, el octaedro es convexo y se denomina regular, siendo una figura de los
llamados sólidos platónicos.

3. Concepto:

Un octaedro es un poliedro regular formado por 8 triángulos
equiláteros iguales.

Se puede considerar formado por la unión, desde sus bases, de
dos pirámides cuadrangulares regulares iguales.

4. Propiedades del octaedro.
Número de caras: 8.
Número de vértices: 6.
Número de aristas: 12.
Numero de aristas concurrentes en un vértice: 4

5. Formulas.
 Área del octaedro
 Volumen del octaedro

6. 
Se llama octaedro porque es un poliedro con 8 (octa-) caras (igual
que un octópodo tiene 8 tentáculos)

7.  Cuando decimos "octaedro" normalmente
queremos decir "octaedro regular" (es decir,
todas las caras tienen el mismo tamaño y forma),
pero no tiene por qué serlo siempre: este
también es un octaedro, aunque sus caras no
sean todas iguales (pero es mejor llamarlo
prisma hexagonal).

8.  ¿Dados de 8 caras? ¡Sí! Un octaedro con 8 caras
iguales tiene la misma probabilidad de caer sobre
cada una de las caras.
 De hecho, puedes hacer dados equilibrados con
todos los sólidos platónicos.

9. Volumen, área y desarrollo.
vértices = 6Cubo.
Simetría = Octaédrico (Oh).Dado un octaedro regular de arista a, podemos
calcular su volumen V.

10. Simetría
 Un octaedro regular tiene tres ejes de simetría de orden
cuatro, las rectas que Simetrnen vértices opuestos; seis ejes
de simetría de orden dos, las rectas que unen los centros de
aristas opuestas y cuatro ejes de simetría de orden tres, las
rectas que unen los baricentros de las caras opuestas; nueve
planos de simetría, tres que contienen cada grupo de aristas
coplanares, y seis perpendiculares a cada par de aristas
paralelas; y un centro de simetría. Los elementos de simetría
anteriores definen uno de los grupos de simetría
octaédricos, el denominado Oh según la notación de
Schöenflies.

11. Proceso para hacer un ejercicio.
1 - Desde el punto F se traza una recta que forme 60º con la línea
de tierra.
2 - Se halla la traza horizontal de esa recta, que será el punto E, y
por tanto ya se tiene la diagonal del cuerpo, FE.
3 - Por el punto medio de FE se hace un plano perpendicular o
uno que sea perpendicular al primer bisector y forme 30º sus
trazas con la línea de tierra, lo mismo es.
4 - Se abate el plano y el punto medio de FE.
5 - En el abatimiento se dibuja el cuadrado ABCD con centro en
el punto medio de FE, cuya diagonal sea igual a la verdadera
magnitud de FE y que formen (sus diagonales) 45º con
respecto a la traza horizontal del plano.
6 - Desabatir el cuadrado y unir sus vértices con E y F.

12. Dibujo: