(1) El documento describe los conceptos de presión, presión absoluta y manométrica, y la relación entre presión y elevación. (2) Explica cómo calcular la fuerza resultante sobre un área plana debido a la presión de un fluido, usando la presión promedio. (3) Proporciona procedimientos para calcular la fuerza sobre paredes rectangulares y rectangulares inclinadas debido a la presión de un fluido.

![UMSA-FACULTAO DE INGENIERIA OPERACIONES UNITARIAS PET-245
PROBLEMAS RESUELTOS
P-1.1 Un líquido de peso especifico l.2S [g/cm
3
], llena parcialmente el reservorio esférico
de la figura . ¿Cuál será la intensidad de la presión en un punto situado a O.SS [m] debajo
del punto C (punto D)?
SOLUCION:
B
o.38 lmJ
y1= 1.25 [g/cc]
y2=13.6 [g/cc]
(2)y(3) en......(1)
Re ernplazando :
101325 ~ - 0.38111*(13600 *9.81) ~ =P0 - 0.55111 *(1250 *9.81) ~
m m m
P0 = 57.37 KPa presion. absoluta
P-1.2 Calcular la diferencia de presiones entre los puntos 1 y 2 de la tubería de la figura
por la que circula agua, el líquido en el piezómetro tiene una densidad relativa de 2.96,
(Tome como datos adicionales h=0.6m, z=O.Sm)
Gula Aux. José Luis Huanca P. Página 2
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-2-320.jpg)

![UMSA-FACULTAO DE INGENIERIA OPERACIONES UNITARIAS PET-245
P-1.3 Para el tanque que muestra la figura calcular el valor de H.
SOLUCION: (+!,-i )
p ag,w +<)ªS"". g. 0.2 - <)Hg . g. /-J +Ó. g. 0.3 =~,ceite
30cm
t
Aceite
16(kPa)
H =P,,guil- p aceil, +(8ª8"" •0.2 +() •0.3)g
81/g • g
H = 40- 16+(9810 ·0.2+9810·0.92·0.3) = O. l
743
(ni)
13.6·9810
1
H =l7.43(1n)1
Agua
40(kPa)
20cm
mercurio
P-1.4 Encontrar la diferencia de presiones entre los puntos M y N en función de z, s,h;
( s = r' l
r
SOLUCION:
r
Balance entre los puntos M y B
P.11 =PB - Y* m.....(1)
Balance entre los puntos C y N
M
-·1•· z
,n
Balance entre los puntos By C h +
_
________
P8 =P
e + y'*z .......(3) N
---•--
(1) + (2)
P = P -y*m
]
M B ⇒ P + P = P - y* ,n+ P - r* n
P, - P _ * M e s ,v
C - N Y n,
r'
Por geometría: h-,n = n-z➔ h+ z= 1n+n. .....(5)
Gula Aux. José Luis Huanca P. Página 4
r
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-4-320.jpg)
![UMSA-FACULTAO DE INGENIERIA OPERACIONES UNITARIAS PET-245
~1 - PN =r'*z- r*(h+ z)
r'
Pero: s = - ➔ r'=s*r ⇒ P.w -PN=s*r*z - r*(h +z)
r
PM -P
N =r* [s*z- (h+ z)] ⇒
P-1.S Un piezómetro conectado a un tanque contenido agua como se muestra en la figura,
el liquido en el piezómetro es mercurio (Dr= 13.6). Cuando la superficie del tanque esta
en A, el valor de Hes 0.6(m). Hallar el valor de H cuando la superficie del agua en el
tanque esta en B=S(m) sobre A.
SOLUCION:
Inicialmente en el nivel D se cumple:
Patrn +y* z=Patn1 - y*Ji
r• 13.6 . o6 8 6
z= - *h= --"' . = .l (1
n)
r l
Luego en la situación final cuando el
nivel del agua en el tanque esta en B. el
punto D baja una distancia Y, lo mismo
ocurre con el punto C por lo tanto en el
nivel D se cumple.
z
8
A
1-- -·-------·
-
h=0.6 (m)
- -------------------- 1- -- ~ -·
Gula Aux. José Luis Huanca P. Página 5
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-5-320.jpg)

![UMSA-FACULTAO DE INGENIERIA OPERACIONES UNITARIAS PET-245
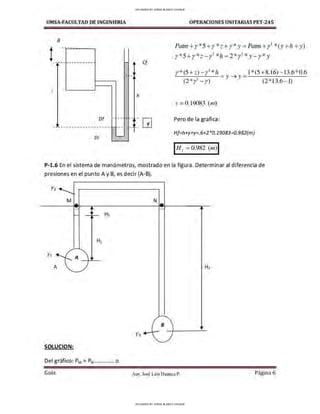
P-1.8 Un liquido A tiene un peso especifico de 9.4 KN/m3 y el liquido B tiene un peso
especifico de 11.4 KN/m3. El líquido manométrico es mercurio. Si la presión de B es de
210 KPa, halle la presión en A:
SOLUCION:
kN kN kN
P¡ = P8 - 6l.56- , = 210- , - 61.56- , =148.44kPa
,n- ,n- m-
Donde:
9.4tNhn3
~
400mm
2m
P6 P5
♦
( A (Hg)=13.6
----------
___,/
3 m
'11.4kNhn3
Por otra parte se tiene P3:
____________
{B_
Donde:
P1 = Pi +11.4 k~ *0.4,n =l48.44kPa +4.56kJ)a =153kJ)a
m
Se tiene P5 bajo la siguiente relación:
~ =P; +13.6*9.81 kN_ *0.4rn
mº
kN k1V kN
P; =~ - 53.37 ~ =153- 2
- 53.37~ =99.63kPa
rn rn m
Sabiendo que:
La presión en el manómetro A es:
PA=Pr, +9.4 ktv_ *2.4m
mº
PA= 99.63k~ +22.56k~ =122.19 [kPa]
nr rn-
IPA=122.19 [kPa]I
Gula Aux. José Luis Huanca P.
J
Página 8
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-8-320.jpg)







![UMSA-FACULTAO DE INGENIERIA OPERACIONES UNITARIAS PET-245
PROBLEMAS RESUELTOS
P-2.1 Cuál es el empuje que se ejerce por el agua en una compuerta vertical de 3 x 4 [m]
cuyo tope se encuentra a S[m] de profundidad.
[
/(9]
YHzO =1000 m3
S[m] S[m]
ji
eg_____ __
CP" ··---- ---------------------------------------------------.iJ
SOLUCIÓN:
4[rn]
En el problema: h = y= 1.S[m] + 5.0(m] =6.S(m]
A= (3 x 4)[m] = 12(m2
)
E = yhA = 1000 [~[ ] x 6.S(m] x 12 (m2
]
1
E = 78000[Kgr ]
1
Cp
P-2.2 Determine la posición del centro de presiones para el caso de la compuerta del
problema anterior.
- fo
Yp=y + yA ... ... ... ... ... ... .... (a)
Donde: f0 = momento de inercia con respecto al centro de gravedad
1 1
/ 0 =
12
bh3
=
12
(4m)(3m)3
= 9[m4
] .. ....... ... ...... ......... ... (/3)
{3 en a
9[m4
]
Yp = 6.S[m] + ( )( 2 )
6.Sm 12m
P-2.3 Determine la coordenada del centro de presion (Cp) de las siguientes áreas situadas
en planos verticales y la magnitud de la fuerza F
Gula Aux. José Luis Huanca P. Página 16
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-16-320.jpg)

![UMSA-FACULTAO DE INGENIERIA OPERACIONES UNITARIAS PET-245
P-2.4 Un dique con 4[m] de altura y lO[m] de ancho presenta un perfil parabólico aguas
arriba. Calculé se la resultante de la acción del fluido. (Solución numérica).
SOLUCIÓN:
H,0
/¡ =4n1I F,,
--+--+---
1.5,n
Componente Horizontal:
h
FH =y. - . b. h
2
X
F
' N
'
►
IFy
1
A 1-
2.511'1
F11 Fx
[
Kgf] 2
Fv =1000 m3 •
3·1.S[m] · 4[m] · lO[m]
F,, =40000 [Kgf] *
[
Kgf] 4
Flf = 1000 m3
•
2
[m] · 4[m] · lO[m] Donde se aplica: (x)
5 5
i = Xp =
8
· r =
8
· 1.S[m]
Donde se aplica: Xp =0.94[m]
2 2
Yp = 8
• h; Yp = 8
• 4[m] Para la resultante {R)
Yp =2. 67 [m] *
Componente Vertical: R = Jcaoooo)2 + (400000)2
Fv = y ·Aso · b = y · (!r · h) · b
R = 89442. 7 [Kgf] *
Gula Aux. José Luis Huanca P. Página 18
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-18-320.jpg)
![UMSA-FACULTAO DE INGENIERIA OPERACIONES UNITARIAS PET-245
P-2.5 La compuerta de la figura .Tiene 3 [m] de longitud. Calculé se la magnitud y
ubicación de los componentes de la fuerza que actúan sobre ella.
,,..._, ,,..._, ,,..._,
,,..._, ,,..._, ,,..._,
A w e
,,..._, ,,..._, ,,..._,
Solución: Calculo de la Fuerza
Horizontal.
Fh =y. h. AAB
FH = (~)- b · h
2
Yp = 3
· 2[m]
Yp = 1.33[m] *
Calculo de la fuerza Vertical:
Fv =y· V
Fv =y· AAB · b
[
Kgf] 2
FH =1000 m3 •
2
[1n] · 3[1n] · 2[1n] (
rr. h
2
)
Fv =y·
4
· b
F1t = 6000[Kgf] *
Calculo de Yp:
l
Yp =Ycg +y; . A
cg CB
h b · h3
Yp =2+ 'h
12 · (2) · b · h
h h
Yp =2 + 6
2
Yp =3·h
Gula
Fv =9424.B[Kgl] *
Calculo del lugar donde se aplica (x)
4 · h
x=--
3n
_ 4 · 2[m]
x=---
3n
X = Xp = 0. 849[m]
Aux. José Luis Huanca P. Página 19
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-19-320.jpg)




![UMSA-FACULTAD DE lNGENIERIA
1l'D2 1r(450f 3
Vy = 4 · L = 4 ·6.750 =1.074111
[
;rr/)2 fJ ] ]
Vt1 = - ·-+-(2xx115
) L
4 360 2
V = [ ¡z-(0.4
5
)2 . 2415
+ .!_(0.!934y0.l 15)]6.75rn3
= 0.8703ni3
J 4 360 2 ~
Yum>d =(9.8lkNI 1
n
3
xo.8703/1.074)=7.95kN/ 1
n
3
Ywotul =7.95kN/ ,n3
OPERACIONES UNITARIAS PET-245
P-2.11 En la siguiente figura, un cilindro de 2,4 m de diámetro cierra un agujero
rectangular en un depósito de 0,9 m ¿Con que fuerza queda presionado el cilindro contra
el fondo di deposito por la acción de los 2.7 m de profundidad de agua?
2 .1 m
FIGURA
Pv =fuerza hacia abajo sobre CDE - fuerza hacia arriba CA y BE
= 1000*0.9[(21*24 - .!_.ir*12
2
) - 2(21 * O162 + -
1
;r *12
2
- .!_*O6*l 038)]
' ' 2 ' ' ' 12 ' 2 ' '
=2500-810=1690 [ kg hacia abjo ]
Guía Aax. José Luis Huanca P. Página 24
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-24-320.jpg)

![UMSA-FACULTAD DE lNGENIERIA OPERACIONES UNITARIAS PET-245
donde x e y son las coordenadas, en metros, de un punto genérico de la superficie,
medidas con el origen en el vértice situado en el eje de revolución, y "w" la velocidad
angular constante, medida en radianes por segundo. La demostración de esta fórmula se
da más adelante.
• RECIPIENTES CERRADOS
En los recipientes cerrados aumenta la presión al girar los recipientes. El aumento de
presión entre un punto situado en el eje y otro a una distancia de x metros del eje, en el
mismo plano horizontal, es:
(j)2 ?
p = y- x-
2g
y el aumento de la altura de presión (m) será
que es una ecuación análoga a la aplicable a recipientes abiertos en rotación. Como la
velocidad lineal v=x*w, el término x
2
w
2
/2g = v
2
/2g da la altura de velocidad, en m, como
se verá más adelante.
PROBLEMAS RESUELTOS
P-3.1 Problema: Un vaso de 1.22[m] de diámetro está abierto y lleno de un liquido como
muestra la figura . Determinar el volumen derramado del liquido cuando el cilindro gira
sobre su eje vertical simétrico.
SOLUCIÓN:
w
1
4 y ~
,
D = 1.22[m]
Guía
H =1.83[m]
.
..
Aax. José Luis Huanca P.
w =60rpm
2n 1S
w =60rpm* - - *-
60rpn, l m
w = Zn[rad]
2
Y =~ *x2
2•g
y= Q.75[m] Altura del paraboloíde
Página 26
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-26-320.jpg)
![UMSA-FACULTAD DE lNGENIERIA OPERACIONES UNITARIAS PET-245
H =y+ h ~ h = H - y= (1.83 - 0.75)[m]
h =l .08[n1..]
Vderra,nado =Vparaboloide de rebolucion
1
Vparaboloide de reboluclon = 2
Vcilindro circunscrito
1 2
Vderraniado = 2
(n:r )y
1 2 3
Vderr,m11td o =
2(n:0.61 )0.75 m
Vderramado =O. 44m
3
Rpta.
P-3.2 Un vaso cilíndrico abierto está lleno de líquido. ¿A qué velocidad deberá girar sobre
un eje vertical para el liquido deje descubierto en el fondo un circulo en el fondo de radio
(3R/4) del cilindro. ¿Cuál será el volumen del líquido derramado con esta relación? El vaso
tiene 1.6 (m) de diámetro y 2(m) de altura:
SOLUCIÓN:
w2 z
H =Zg(R ) ... ... ... (1) Y =;; (!R)
2
...... . .. ........... (2)
pero H = 2(m) +Y ... ...... (3) remplazando (l )y (2)en (3)
w
2
R
2
w
2
(3 )2
w
2
R
2
( 9)
- - =2+ - - R - - 1 - - =2
2g 29 4 29 16
w2R2(!_) - 2_6+g
29 16
- 2 W -
7
R2 con10 R = 1,6(m) y 9 = 9,81 m/s2
.
.. W=
64 * 9,81cm/s2)
7 * (1,6(m))2
rad
W =5.92-
s
para el volumen: Vderra,nado =Vparabota
1 2 1 2
Vderramado1 =
2rcR H =
2n:(0,8) * 4.SS(m) = 4.574(m) ......... (1)
1 3 2
Vderramado2 =
2rc (¡* 0.8) * 2.SS(m) = 1.442(m3
) ............... (2)
Vderramado(Total) = Vdl - Vd2 = (4.574 - 1.442)(rn3
)
Vderramculo(Total) = 3. 13 (m3
)
Guía Aax. José Luis Huanca P. Página 27
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-27-320.jpg)


![UMSA-FACULTAD DE lNGENIERIA OPERACIONES UNITARIAS PET-245
CAPITULO 4
"FLUJO DE FLUIDOS Y LA ECUACION DE BERNOULLI"
4.1 RAPIDEZ DE FLUJO DE FLUIDO
Es la cantidad de flujo que fluye en un sistema por unidad de tiempo, se puede expresar
mediante los tres términos que definimos a continuación.
La Rapidez de Flujo Volumétrico (Q), es el volumen de flujo de fluido que pasa por una
sección por unidad de tiempo y esta es la más importante entre los tres términos que se
menciona y se calcula empleando la siguiente ecuación:
Donde:
A = es el área de la sección
V = es la velocidad promedio del fluido
4.2 LA RAPIDEZ DE FLUJO DE PESO (W), es el peso de fluido que fluye por una sección
por unidad de tiempo y está relacionada con Q mediante la ecuación:
DONDE:
W= r *Q
IW = r* A *v ]
W = es el peso específico del fluido
Q = es la rapidez de flujo de volumen
4.3 LA RAPIDEZ DE FLUJO DE MASA (M), es la masa de fluido que fluye por una
sección por unidad de tiempo y está relacionada con Q mediante la ecuación:
M=p * Q
IM= p * A *v i
Donde:
p = es la densidad del fluido
Q = es la rapidez de flujo de volumen
Guía Aax. José Luis Huanca P. Página 30
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-30-320.jpg)





![UMSA-FACULTAD DE lNGENIERIA OPERACIONES UNITARIAS PET-245
PROBLEMAS RESUElTOS
P-4.1. En la siguiente figura, están circulando 0.370m3
/s de agua de Aa B, existiendo en A
una altura de presión de 6.6 m. Suponiendo que no existen perdidas de energía entre A y
B determinar la altura de presión en B. Dibujar la altura de líneas totales.
o
Línea de altura•
s totales
- =0.09111
Vb"
-,:----.-------"'------ - - - - - -- - 2g
"· 6.6111
y
z,, 3.0111
Línea de alturas piezométricas _ , _ . - . - · - · - · - · - · -
.- -- -- ·- ·- ·-·- · P. -3.41111
-------r----..,..Jh. 3.41111
r
B60cm
A30cm
Plano de referencia z. =7.5111
o
FIGURA
(P
.
4 V
2
30 z )-(Pu V-,o z )
- +- -+ A - - + - - + 8
r 2g r 2g
Donde: V30 = O/ A30 = 0,370[{1!4)ll'0.32
]=5,24m/sy
V60 = (~)
2
{5,24)= l,3lrn/.v.Sustituyendo,
( 6,6+ (5,24)
2
+OJ=(Pu + (1,31)
2
+ 4,sJ y
2g r 2g
P
u= 3,41m de agua
r
Puede representarse la energía total en una sección cualquiera como altura sobre un
plano horizontal de referencia. Utilizando en este caso el plano que pasa por D-D.
Altura total en A =P,1/r+ V
2
30/2g +zA = 6,6+ l,4 + 3,0 = ll,O,n
Altura total en B = p 8 / Y + V 2
6-0/2g + Z8 = 3,41 + 0,09 +7,5= 11,0,n
Guía Aax. José Luis Huanca P. Página 36
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-36-320.jpg)
![UMSA-FACULTAD DE lNGENIERIA OPERACIONES UNITARIAS PET-245
Nota: Se observa que tiene lugar la transformación de una forma de energía en otra
durante el flujo. En el caso presente, parte de la energía de presión y de la energía cinética
en Ase transforma en energía potencial en B.
P-4.2 Según la figura mostrada determinar el caudal y la presionen el punto A. (Sin tomar
en cuenta las perdidas menores) D1=150mm D2=SOmm
Datos:
D1=150mm
D2=50mm
y=9810[N/m
3
]
Incógnitas:
a) Q?
b) PA=?
Guía
- _
e ------
-
H ,O 2,4111
•
----·-
D 3,6111
♦D,
1
•A e B
t
SOLUCION:
a) La velocidad de las partículas en Ces tan pequeña que puede
despreciarse. Para calcular el caudal Primero:
Ecuación de energía entre C y B:
P. v1 P. v 2
_í + e + Z = -1!.. + - 8
- +Z
r 2g e r 2g 8
?
O+(desprec.) +(3,6 + 2,4) = 0 + v8
- +O(nivel de referencia)
2g
Despejando la velocidad en el punto B
VB=.J2g *(3,6 + 2,4) = .J2 *9.81*(3,6 + 2,4) =L0.85[:
1
]
Según la siguiente ecuación se calculara el caudal en la tubería:
1r , rn 1r , rn3
Q8
= V * A = V * -D8
- = 10.85-*-(0.0Srn)- = 0.021-
4 s 4 s
3
Q = 0.021 'n
s
b) Para cálculo de la presión analizando la variable Ps/y=O (da a la
atmosfera).
Ecuación de energía entre los puntos A y B
Aax. José Luis Huanca P. Página 37
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-37-320.jpg)

![UMSA-FACULTAD DE lNGENIERIA OPERACIONES UNITARIAS PET-245
2(9.81rn/2 )(5.67m - 4.73rn)
V
_ I s
.- 1
Para la velocidad del agua será:
vi( /) =0,98*4.291
,nlJ--
► v i(,"'''') = 4,2J. _rri/
.r .
,w, · [¡ 8 • -/s
P-4.4. En el venturímetro la lectura del manómetro diferencial, en el fluido es 35,8 (cm)
determine el caudal de agua a través del venturímetro si se desprecia las pérdidas entre
los puntos A y B.
SOLUCIÓN:
Aplicando la ecuación de Bernoulli
p 12 p 12
__i_+ - "
- + z =_IL+ _E_ + z
r 2g A r 2g º
'
~~,¡
' ' 1
1 ' •
. ' '
. ' .
' '
A
Q=?
Z8 =0,75~11]
? ?
~ :====:::::;-,
P,1 v;¡ - Po Vñ O ( )
- + - - - +- + t75 ...................... 1
r 2g r 2g
Sabemos que: P,.. =P0
p
Pe = __i_+ h + 0.358
r
p
PD= 0,75 + h+ 0.358*13,6 + _1L
r
Entonces:
'
'
B
•
''•
p p
__i_+ h +0.358 = 0,75 + h+ 0.358 *13,6 + _lL
r r
PA= 5,2608+ Po .................................... (2)
r r
(2) en (1)
p 11
2 p 11
2
5 26Q$ + _IL + _A
_ = _IL + - 8
- + () 75
' . ,
r 2g r 2g
2 2
VA Vo
- =- - 4,7.l ......,................................ (3)
2g 2g
De la ecuación de conductividad tenemos: AA*VA = A8 * V 8
Guía Aax. José Luis Huanca P.
T
)Sc11,
h
t
I
Página 39
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-39-320.jpg)

![UMSA-FACULTAD DE lNGENIERIA OPERACIONES UNITARIAS PET-245
b) Empleando Bernoulli en los puntos Sy A:
Ps v] PA vl
-+z5 +-= -+zA+- Pc= O
YAc 29 YAc · 29 '
Despejado la presión en A
[
v
2
- v
2
]
PA = s
29
A+ (zs- zA) *YAc ... •·········(1)
Donde la VAse la obtiene empleando la ecuación de continuidad:
rr * (0.035m)2
7 6 7
m 3
Ac * Ve 4 * · s . m
QA = QB => VA = A,, = rr * (0.lm)Z = 0.904 s
Sustituyendo VA en (1):
O- (0.94 rn)2
----"-~-
1
-+ (4m - O
)
2*9.812
s
Empleando Bernoulli entre los puntos Sy B:
4
kN
* 0.85 * 9.81 3 = 32. 98 kpa
m
Ps v] P8 vJ
- +zs+ - = -+ zB +-
Y11c 29 YAc 29
Considerando Ps=O y despejando Ps:
Vs - VB
[
2 2 ]
PB = 29
+ (zs - zB) * YAc •·· •·· •·· •·· ...... (2)
Sustituyendo la V8 en (2) se tiene:
o - (0.947)2
P8 = m + (3.0ni - O
)
2 *9.81 2 9
s
m
" 0.85 * 9.81(2)
s
P-4.6 Para el sifón que se muestra en la figura calcule a) la rapidez de flujo de volumen de
aceite del tanque y b) la presión en los puntos A, B, C, D.
Guía Aax. José Luis Huanca P. Página 41
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-41-320.jpg)
![UMSA-FACULTAD DE lNGENIERIA OPERACIONES UNITARIAS PET-245
t
/ +a
3.0m
1
1
--- + +
--- A. e
-
---
Aceite
(sg =0.86)
10.0m 50mm
- de di:1mctro
SOLUCION:
a)
T - - '
n1
V 2 = -J2g(z1 - Z2) = V2 * 9.81 * 10 =14.01 -
S
donde
V2
VA =VB = Ve =Vv =-4
.._
n(0.25)2
_
3
nt3
Q=A2 v2 = 4
* 14.01 = 6.88 * 10
5
interior
+ D
[ v}] ( 3.502
2
)
PA = Y
0 - - = 0.86 * 9.81 - - - - = - 5.27 kpa
· 2g 2 *9.81
25 mmde
dlámetro
interior
1
f
---
- -
PB =Yo [cz1- ZB)- ;;] = 8.437 * (- 3 - 0.625) = - 30. 58 kpa
Pe =PA = - 5.27Kpa
2 2
P1 V1 Pv Vv
- + Z1 + - = - + Zv + -pl = 0 , V1 = 0
Yo 2g Yo 2g
Po= Y
0 [(z1 -z0 )- ;;] = 8.437 * (10 - 0.625) = 79.1 kpa
2
m
VA= 3.502-
S
P-4.7 En la figura se muestra un manómetro que se utiliza para indicar la diferencia de
presión entre dos puntos de un sistema de conductos. Calcule la rapidez de flujo de
volumen del agua del sistema si la desviación en el manómetro es h de 250 mm (A este
Guía Aax. José Luis Huanca P. Página 42
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-42-320.jpg)
![UMSA-FACULTAD DE lNGENIERIA OPERACIONES UNITARIAS PET-245
dispositivo se le conoce como medidor Venturi, que se utiliza a menudo para mediciones
de flujo).
SOLUCION:
A
Díreccion de Hujo
B
...-
,,..
---_-_--;-, t-___.......____
~ mm 0$ 11am~
- - - + - 1 ll'll!!r10r
h
Mercurio
p 2 [.> 2
_ A + Z + VA = -1!.. + z + v /J ·Z = Z
A 2g /J 2g ' .4 /J
r.,, r.,.
~ ~
PA-PB - Va- - vA- [vA(AAIA8)]
2
- vA
2
= [vA(DAID8J f- vA
2
r,,, 2g 2g 2g
2g 2g
Del manómetro:
PA+r,,,Y+r,,,h - rHgh - r..,y =PB
PA-P8 =rH
gh- r.,,h =h(rHg - r11
.) =1i(13.54r.,. - r..,)=1i(12.s4r.,.)
?
PA- P8 _ 15vA-
r.. 2g
12.S4r ,,,h _ 15vA
2
-
r.,, 2g
2g ·12.54 ·h
V - - - - - - -
A - 15 -
2·9.81,n/s 2
•12.54•0.250m
2025 1
,___________ = . ,n s
15
Guía Aax. José Luis Huanca P. Página 43
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-43-320.jpg)




![UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Aux. José Luis Huanca P. Página 48
Donde:
f = Factor de fricción de Darcy, adimencional, usualmente el número varía entre 0.008 y
0.10
L = Longitud de la tubería, ft
D = Diámetro interno de la tubería, ft
V = Velocidad media del liquido, ft/s
g = Aceleración debido a la gravedad, 32.2 ft/s2
en unidades inglesas
En un flujo laminar, el factor de fricción f solo depende del número de Reynolds. En un
flujo turbulento f depende del diámetro de la tubería, de la rugosidad de la tubería y
del número de Reynolds, como se mostrara.
5.8 FACTOR DE FRICCIÓN
Para flujo laminar, con un número de Reynolds R<2000, el factor de fricción de Darcy es
calculado mediante la siguiente relación:
Para un flujo laminar el factor de fricción solo depende del número de Reynolds y es
independiente de las condiciones internas de la tubería.
Para un flujo turbulento, Cuando el numero de Reynolds es R > 4000, el factor de fricción
f no solo depende del número de Reynolds, sino también del la rugosidad en el interior de
la tubería. Dado que la rugosidad incrementa, así también los hace el factor de fricción.
Por eso una tubería lisa tiene menor factor de fricción comparada con una tubería rugosa.
Mas correctamente, el factor de fricción depende de la rugosidad relativa (e/D) donde e
es la rugosidad absoluta de la tubería.
Existen varias relaciones para hallar el valor del factor de fricción f . Estos están basados
en experimentos realizados por científicos e ingenieros en los últimos 60 años. Una buena
ecuación propuesta para un flujo turbulento (donde R>4000) es la ecuación de Colebrook-
White:
[
√
]
Donde:
f=Factor de fricción de Darcy, adimensional
D=Diámetro interno de la tubería, in.
e=Rugosidad absoluta de la tubería, in.
R=Numero de Reynolds, adimesional
Todos los términos en la ecuación son adimensionales
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-48-320.jpg)
![UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Aux. José Luis Huanca P. Página 49
Esta ecuación puede verse que el cálculo no es fácil, dado que el factor de fricción f
aparece en ambos lados de la ecuación. Para lo cual se debe resolver con un error. Se
puede empezar a asumir un valor de f (0.02) y sustituir en el lado derecho de la ecuación.
Esto llevara a una segunda aproximación de f, la cual puede ser usada para re calcular el
valor de f por sucesiva iteración. Generalmente, de tres a cuatro iteraciones pueden dar
un valor satisfactorio de f. (correcto con 0.001 decimales)
Durante las dos últimas décadas varias formulas del factor de fricción para flujo
turbulento han sido propuestas por varios investigadores. Todas estas facilitan el cálculo
del factor de fricción comparada con la ecuación de colebrook-White estas requieren un
error y son llamadas ecuación de Churchill y Swamee-Jain.
En la zona critica, donde el numero de Reynolds está entre 2000 y 4000, Generalmente la
formula no es aceptada, esto es debido a que es una zona inestable y por eso el factor de
fricción es indeterminado. Pero es más comúnmente calculado como si fuera flujo
turbulento.
Para denotar mejor, la zona de flujo turbulento (R>4000) actualmente consiste en tres
diferentes zonas:
Flujo Turbulento en tubería lisa
Flujo Turbulento en tubería totalmente rugosa
Flujo de Transición en una tubería lisa y rugosa
5.8.1 Para flujo turbulento en tubería lisa, La rugosidad en la tubería tiene un efecto
despreciable en el factor de fricción f. Por eso, el factor de fricción en esta región solo
depende del número de Reynolds como sigue:
[
√
]
5.8.2 Para Flujo Turbulento en tubería totalmente rugosa, el factor de fricción f parece
depender menos del numero de Reynolds como la rugosidad aumento de valor. En este
caso solo dependerá de la rugosidad y el diámetro. Y este puede ser calculado mediante la
siguiente ecuación:
[ ]
5.8.3 Para la zona de transición entre un Flujo turbulento en tubería lisa y un flujo
turbulento en tubería rugosa, el factor de fricción f es calculado usando la ecuación de
Colebrook-White dado anteriormente:
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-49-320.jpg)
![UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Aux. José Luis Huanca P. Página 50
[
√
]
La ecuación discutida arriba puede ser graficada sobre un Diagrama de Moddy. La
rugosidad relativa es definida como e/D, y es el resultado de simplemente dividir la
rugosidad absoluta entre el diámetro interno de la tubería. Los términos de la rugosidad
relativa son adimencionales. El diagrama de Moddy refleja un mapa completo para la zona
de flujo laminar y turbulento dentro la tubería. El diagrama de Moddy no es confiable
debido a que se usa un error para resolver la ecuación para el cálculo del factor de fricción
f. Para usar el diagrama de moddy, para
Figura Diagrama de Moody para el factor de fricción.
determinar el factor de fricción f. Primero se debe calcular el número de Reynolds R, luego
localizar en el eje horizontal el valor del numero de Reynolds y dibujar una línea vertical
hasta interceptar con la apropiada curva de rugosidad relativa (e/D). Desde este punto de
intersección sobre (e/D), leer el valor del factor de fricción f sobre el eje vertical de la
izquierda.
0.1
1,..
o
.....
u
ro
l.L
e
o
t,
·e V
lL e: Q)
o e
N o
1- N
l'O
e l'O
.E (J
:¡:¡
ro ·e
...J u
2000 4000
Turbulent Zone __.,..
Complete Turbulence
, Rough Pipes
._
Reynolds Number
o.os
~
Q)
e
.e
O'I
::,
ii
(l,J
>
:¡:;
ro
~
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-50-320.jpg)

![UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Aux. José Luis Huanca P. Página 52
P-5.2 Calcule la rapidez de flujo de volumen máximo de aceite combustible a 45ºC a la cual
el flujo seguirá siendo laminar en un conducto de 100mm de diámetro. Para el aceite
utilice SG= 0,895 y una viscosidad dinámica de 4,0 *10-2
Pa-s.
DATOS:
D =100 mm
µ (45ºc)=4,0*10-2
Pa*s
SG= 0,895
INCOGNITAS:
NR=?
SOLUCION:
Considerando flujo laminar NR < 2000
Calculo del caudal empleando la ecuación de continuidad:
[ ]
[ ]
P-5.3 Aire con un peso especifico de 12,5 N/m3
y una viscosidad dinámica de 2,0*10-5
Pa*s,
fluye a través de la parte sombreada del ducto de la figura, con una rapidez de 150 m3
/h.
Calcular el número de Reynolds del flujo.
DATOS:
= , * -5
Pa*s
γ= , N/ 3
Q =150 m3
/h
INCOGNITAS:
NR=?
SOLUCION:
Superficie del área sombreada:
r
50mm
l - - SO mm ----1
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-52-320.jpg)
![UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Aux. José Luis Huanca P. Página 53
{[ ( )] }
Velocidad de flujo promedio:
Perímetro mojado:
√
Calculo del radio hidráulico para sección irregular, para ello se reemplaza los valores de
área y perímetro mojado en la siguiente relación:
Calculo del NR empleando la siguiente relación:
[ ]
P-5.4 En el sistema mostrado en la Figura la bomba BC debe producir un caudal de 160 l/s
de aceite, Dr = 0,762, hacia el recipiente D. Suponiendo que la pérdida de energía entre A
y B es de 2,50 m y entre C y D es de 6,50 m, a) ¿qué potencia en HP debe suministrar la
bomba a la corriente? b) Dibujar la línea de alturas totales.
A
B C
D
cm
D 30
cm
D 30
Figura
m
3
m
60
m
15
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-53-320.jpg)
![UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Aux. José Luis Huanca P. Página 54
D
D
D
perd
B
A
A
A
Z
g
v
P
H
H
Z
g
v
P
2
2
2
2
60
.
0
)
5
,
6
5
,
2
(
15
.
0
desprec
H
desprec B
m
HB 0
.
54
W
m
s
m
m
N
H
Q
Watt
Potencia BOMBA 9
,
64585
0
,
54
*
)
16
.
0
(
*
)
81
.
9
*
1000
*
762
.
0
(
*
*
3
3
HP
W
HP
W
HP
Potencia 58
.
86
746
1
*
9
,
64585
)
(
HP
Potencia 58
.
86
DATOS: SOLUCION:
Q=160 [l/s]
Dr=0,762
HA-B=2,5m
HC-D=6,5m
INCÓGNITAS:
a) Pott=?
b) Líneas de alturas
b)
P-5.5 Una tubería que transporta aceite crudo (SG=0.93) a 1200 l/min está hecha con
conducto de acero de 6 plg, Calibre 80. Las estaciones de Bombeo están espaciadas 3,2
Km entre sí. Si el aceite esta a 10 ºC, Calcule: (a) La caída de presión entre estaciones y (b)
La potencia requerida para mantener la misma presión en la entrada de cada bomba.
a) La velocidad de las partículas en A y D es tan pequeña que puede
despreciarse las alturas de velocidad.
Ecuación de energía entre A y D:
A
B C
D
Figura
m
60
m
3
m
15
m
5
.
66
m
5
.
12
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-54-320.jpg)
![UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Aux. José Luis Huanca P. Página 55
DATOS:
D (6plg)= 146.3 mm (Tabla)
µ (10ºC)= 1.5*10-1
N*s/m2
(Tabla)
SG= 0.93
Q= 1200 l/min
L= 3,2 Km
INCOGNITAS:
a ΔP=?
b) Pott=?
SOLUCION:
a) Caída de presión entre los puntos A y B
Aplicando la ecuación de energía en los puntos A y B:
Despejando de la ecuación de energía la diferencia de presión se tiene:
[ ]
Velocidad en el conducto:
[ ]
[ ]
Se sabe que la perdida de energía (hL) en el conducto es:
Numero de Reynolds:
Calculo de factor de fricción:
Q
Flujo
Bomba Bomba
m
3200
A B
A
P
esion
Pr B
P
esion
Pr
aC).i----------::-----On
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-55-320.jpg)
![UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Aux. José Luis Huanca P. Página 56
Sustituyendo el factor de fricción f en (2):
Reemplazando la pérdida de energía en (1):
[ ] [ ]
[ ]
b) Calculo de la potencia de la bomba para mantener la misma presión a la entrada
de cada bomba.
P-5.6 A través de una tubería nueva de fundición esta circulan de agua a 20°C y a una
velocidad de 4,2(m/s), la tubería es de 150mm de diámetro y tiene una longitud de 400m.
Determine la perdida de carga debida a la fricción.
DATOS:
SOLUCIÓN:
Calculo del Número de Reynolds:
Diametro D
Presion P
i() Temperatura T¡
( ) ~· esion P2
R ujo Q
1· ·I
Longitud L
0 0
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-56-320.jpg)


![UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Aux. José Luis Huanca P. Página 59
)
4
.....(
..........
Re
51
.
2
71
.
3
log
2
1
cal
cal f
D
e
f
]
[
26 cm
D
Ecuación de Colebroock:
Este valor de f(supuesto) coincide con el valor de f(calculado). De aquí que el valor correcto de
D diá et o e ue ido es .
P-5.8 Para una tubería de acero de 4 pulgadas Calibre 80 de 25 pies de longitud está
fluyendo agua a 100ºF. Calcule la velocidad de flujo de volumen máxima permitida si la
pérdida de energía debido a la fricción de la tubería se limitará a 13.061 pies lb/lb.
Encontrando los valores:
4" 0.3188[ ]
D pies
, 4
1.5 10 [ ]
pies
, 6 2
7.37 10 [ ]
v pies s
SOLUCION:
Despejando de Darcy la velocidad de flujo expresado en función de f:
2
f
2
L
L V
h
D g
⟹
2
f
L
h D g
V
L
2 2 2
13.061[ ] 0.3188[ ] 2 32.2[ ] 10.726[ ]
25[ ] f f
pies pies pies s pies s
V
pies
(1)
Número de Reynolds en el conducto en función a la velocidad de flujo:
4
4 2
0.3188[ ]
4.326 10
7.37 10 [ ]
R
D V m V
N V
v pies s
(2)
Rugosidad relativa:
f(supuesto) D ec. 1 Re ec. (2) e/D ec. (3) f(calculado) ec.(4)
0.020 0.24999 1251081.8 0.002000 0.024
0.024 0.25928 1209176.3 0.001928 0.024
Para el cálculo del diámetro se procederá:
. “e efe tuara el ál ulo por ta teo de u valor f(supuesto) fa tor de fri ió , deter i a do D por la
ecuación (1).
2. Se determinara Re y (e/D) para el valor de D o las e ua io es y .
. “e deter i ara el valor de f(calculado) e fu ió de Re y e/D o el diagra a de Moody o o la
ecuación de colebroock. En caso de que este valor coincida con el valor del supuesto este será el diámetro
us ado, e aso o trario será e esario efe tuar u uevo ta teo, supo ie do ahora el f al ulado.
/
F
✓-----/ ✓~-/
/
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-59-320.jpg)
![UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Aux. José Luis Huanca P. Página 60
4
4
10
7059
.
4
]
[
3188
.
0
]
[
10
5
.
1
x
pies
pies
x
D
Con el NR y la rugosidad relativa se procede al procedimiento de iteración mediante la
ecuación de colebroock con valores de prueba inicial de f ó también del diagrama de
Moddy f 0.023
y sustituyendo f en (1)
2 2
10.726[ ]
21.6[ ]
0.023
pies s
V pies s
El número de Reynolds se obtiene sustituyendo la velocidad de flujo en (2)
4 5
4.326 10 21.6 9.34 10
R
N
Obteniendo el nuevo factor de f 0.0175
y sustituyendo en (1)
2 2
10.726[ ]
24.76[ ]
0.0175
pies s
V pies s
Cálculo del nuevo número de Reynolds bajo la sustitución de V en (2)
4 5
4.326 10 25.12 1.087 10
R
N
Obteniendo nuevo factor de f 0.017
En vista que el valor de f permanece inalterado que la anterior prueba por tanto se acepta
la velocidad de flujo de 25.12[ ]
pies s
Cálculo de la velocidad de flujo de volumen:
2
0.3188[ ]
25.12[ ]
4
pies
Q AV pies s
⟹
3
2.0[ ]
Q pies s
P-5.9 A través de una tubería de acero con un diámetro exterior de 2pulg y un grosor de
pared de 0.083 pulgadas se encuentra fluyendo un aceite hidráulico. Una caída de presión
de 68 kPa se observa entre dos puntos en la tubería situada a 30m entre si. El aceite tiene
una gravedad especifica de 0.90 y una viscosidad dinámica de 3.0×10-5
m. Calcule la
velocidad de flujo de aceite.
✓--/ /
✓--/ /
/
/
/ 1
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-60-320.jpg)
![UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Aux. José Luis Huanca P. Página 61
4
5
10
7059
.
4
]
[
046584
.
0
]
[
10
3
x
m
m
x
D
DATOS: SOLUCION:
D=2 pulg
Espesor=0.083 plg
ΔP=68 KPa
LA-B=30m
GE=0.90
δ=3.0*10-5
m
INCÓGNITAS:
V=?
2 2
2 2
A A B B
A L B
REF REF
P V P V
Z h Z
g g
Despejando de la pérdida de energía:
2
2 2
.
( )
2
A B B A
L B A
AC H H O
P P V V
H Z Z
Sg g
Sustituyendo los valores y considerando 0
B A
Z Z
y
2 2
2 0
B A
V V g
2
3
68[ ]
7.702[ ]
0.9 9.81[ ]
L
kN m
H m
kN m
Despejando de Darcy la velocidad de flujo expresado en función de f:
2
f
2
L
L V
h
D g
⟹
2
f
L
h D g
V
L
2 2 2
7.702[ ] 0.046584[ ] 2 9.81[ ] 0.23465[ ]
30[ ] f f
m m m s m s
V
m
(1)
Calculo del Número de Reynolds en el conducto en función a la velocidad de flujo:
4
.
3
0.046584 0.9 1000
1.398 10
3.0 10
AC H
R
D V V
N V
(2)
Rugosidad relativa:
Con el NR y la rugosidad relativa se procede al procedimiento de iteración. Como valores
de prueba inicial de f se obtuvo del diagrama de Moddy f 0.03
y sustituyendo en (1)
Empleando la ecuación de la energía en A y en B
t ·-'A- 3
0m -=--=-..-1
8
,
/
/
/
F
✓------'---
/ ✓ /
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-61-320.jpg)
![UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Aux. José Luis Huanca P. Página 62
2 2
0.23465[ ]
2.797[ ]
0.03
m s
V m s
El número de Reynolds se obtiene bajo el sustituto de la velocidad de flujo en (2)
4 4
1.398 10 2.797 3.91 10
R
N
Obteniendo el factor nuevo de f del diagrama de Moddy f 0.024
y remplazando en (1)
2 2
0.23465[ ]
3.13[ ]
0.024
m s
V m s
Cálculo del nuevo NR bajo el remplazo de V en (2)
4 4
1.398 10 3.13 4.38 10
R
N
Obteniendo el factor nuevo de f del diagrama de Moddy f 0.0235
y sustituyendo en (1)
2 2
0.23465[ ]
3.16[ ]
0.0235
m s
V m s
Cálculo del nuevo NR bajo el remplazo de V en (2)
4 4
1.398 10 3.16 4.42 10
R
N
Obteniendo el nuevo factor de f del diagrama de Moddy f 0.0235
. En vista que el valor f
permanece inalterado que la anterior prueba por lo tanto se acepta la velocidad de flujo
de:
3.16[ ]
V m s
.
P-5.10 En un sistema de procesamiento químico, el flujo de glicerina a 60ºF (sg=1.24) en
un tubo para que este permanezca laminar con un numero de reynolds aproximadamente
igual a 300, pero sin exceder este valor. Determine el tamaño de conducto que
transportara una rapidez de flujo de 0.90 s
pie / . Entonces, para un flujo de 0.90 s
pie /
3
en el tubo que usted ha calculado, calcule la caída de presión entre dos puntos separados
entre si a una distancia de 55.0pies, si el tubo está en posición horizontal.
Valor encontrado. 2
2
/
*
10
*
62
.
4 pie
s
lb
/ /
/ /
/ /
/ 1
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-62-320.jpg)




![UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Aux. José Luis Huanca P. Página 67
Empleando la ecuación de la energía en A y B.
Despejando la perdida de energía (hL) y considerando VA= VB y (PA – PB) = 0
[ ]
Expresando la perdida de energía en términos de velocidad, utilizando la ecuación de
Darcy:
Expresando la velocidad en términos de caudal y el diámetro de la tubería:
Sustituyendo la velocidad de flujo en la ecuación de Darcy ó (3) en (2)
Despejando el diámetro del conducto:
⁄
Sustituyendo los valores:
⁄
⁄
Expresando el número de Reynolds en términos del diámetro:
Sustituyendo los valores:
1. Asumiendo un valor de prueba inicial f = 0,0200.
2. Calculo del diámetro del conducto bajo el sustituto de f en (4)
⁄
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-67-320.jpg)









![UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Guía Página 79
PROBLEMAS RESUELTOS
P-6.1 Determine la pérdida de energía cuando 3
0.04[ ]
m s de agua fluye de un conducto
estándar Calibre 40 de 6pulg en un depósito grande.
SOLUCION:
Encontrando los valores:
6 154.1[ ]
D mm
Coeficiente de resistencia a la salida 1.0
K
Velocidad de flujo en el conducto:
3
2
0.04[ ]
2.145[ ]
(0.1541[ ]) 4
Q m s
V m s
A m
Cálculo de la pérdida de energía:
2
2
2
2.145[ ]
1.0
2 2 9.8[ ]
L
m s
V
h K
g m s
⟹ 0.2345[ ]
L
h m
P-6.2 Determine la pérdida de energía cuando petróleo de una gravedad especifica de
0.87 fluye de un conducto de 4pulg a uno de 2pulg a través de una contracción súbita si la
velocidad de flujo en el conducto mayor es de
4.0[ ]
pies s .
SOLUCION:
Cociente de los diámetros 4 2
D D
4
2
4[ ]
2
2[ ]
D pulg
D pulg
Velocidad de flujo en el conducto de 2pulg:
2 4
Q Q
⟹ 2 2 4 4
V A V A
⟹ 2 2
2 2 4 4
4 4
V D V D
2
2
4
2 4
2
(2) 4.0[ ] 16.0[ ]
D
V V pies s pies s
D
Obteniendo K de tablas mediante interpolación para una velocidad de 16.0 [pies/s] en el
conducto de 2pulg y para un cociente de diámetro de 2, tenemos K=0.34
/
/
/
/
I
/
/
/
/ /
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-79-320.jpg)
![UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Guía Página 80
Cálculo de la pérdida de energía:
2
2
2
2
16[ ]
0.34
2 2 32.2[ ]
L
pies s
V
h K
g pies s
⟹ 1.35[ ]
L
h pies
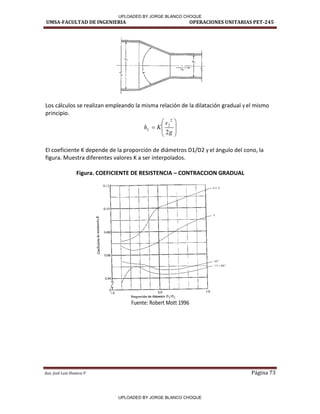
P-6.3 Determine la pérdida de energía para una contracción gradual de un conducto de
acero Calibre 80 de 5pulg a uno de 2pulg para un caudal de 500 [L/min]. El Angulo de cono
para la contracción es 105º.
SOLUCION:
Encontrando los valores:
5 122.3[ ]
D mm
; 2 49.3[ ]
D mm
Velocidad de flujo en el conducto de 2pulg:
3 3
2 2
2
8.33 10 [ ]
4.366[ ]
(0.0493[ ]) 4
Q m s
V m s
A m
Cociente de los diámetros 4 2
D D
5
2
122.3[ ]
2.48
49.3[ ]
D mm
D mm
Obteniendo K de tablas mediante interpolación para un cociente de diámetro de 2.48 y un
ángulo de cono de 105º, tenemos K=0.23
Cálculo de la pérdida de energía:
2
2
2
2
4.366[ ]
0.23
2 2 9.81[ ]
L
m s
V
h K
g m s
⟹ 0.223[ ]
L
h m
P-6.4 Determine la pérdida de energía que ocurrirá si fluye agua de un depósito hacia un
conducto con una velocidad de 3 m/s si la configuración de la entrada es un conducto de
proyección hacia adentro.
SOLUCION:
Encontrando los valores:
Coeficiente de resistencia de entrada 1.0
K
Cálculo de la pérdida de energía empleando la
siguiente relación:
I
/
/
/
/
/
/
/
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-80-320.jpg)
![UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Guía Página 81
2
2
2
3.0[ ]
1.0
2 2 9.81[ ]
L
m s
V
h K
g m s
⟹ 0.459[ ]
L
h m
P-6.5 Determine la longitud equivalente en metros de conducto de una válvula de
compuerta completamente abierta colocada en un conducto Calibre 40 de 10pulg.
SOLUCION:
Encontrando los valores:
10 254.5[ ]
D mm
Longitud equivalente válvula de compuerta 8
Le D
Factor de fricción conductos nuevos de acero 10T
f 0.014
Calculo de K para la compuerta completamente abierta empleando la siguiente relación.
T
= f 8 0.014 0.112
Le
K
D
Determinando la longitud equivalente en metros, empleando la siguiente relación:
8 8 0.2545[ ]
Le D m
⟹ 2.036[ ]
Le m
P-6.6 Calcule la diferencia a través de una válvula de un ángulo completamente abierta
colocada en un conducto de acero Calibre 40 de 5pulg que lleva 650 [gal/min] de petróleo
(sg=0.9).
SOLUCION:
Encontrando los valores:
5 0.4206[ ]
D pies
Longitud equivalente válvula de ángulo
completamente abierta 150
Le D
Factor de fricción conductos nuevos de acero 5T
f 0.016
Empleando la ecuación de la energía en los puntos 1 y 2
2 2
1 1 2 2
1 2
2 2
L
PET PET
P V P V
Z h Z
g g
Despejando la diferencia de presión
/
/
/
1.
/
Válvula de ángulo
completamente abierta
• 2
-
Flujo
6
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-81-320.jpg)
![UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Guía Página 82
2 2
2 1
1 2 2 1
( )
2
L PET
V V
P P Z Z h
g
(1)
Cálculo de la pérdida de energía debida a la válvula de ángulo:
2 2
T
f
2 2
L
V Le V
h K
g D g
(2)
Velocidad de flujo en el conducto:
3
2
1.448[ ]
10.442[ ]
(0.4206[ ]) 4
Q pie s
V pies s
A pies
Sustituyendo valores en la ecuación (2) se tiene hL
2
2
10.422[ ]
0.016 150 4.048[ ]
2 32.2[ ]
L
pies s
h pies
pie s
Reemplazando hL en la ecuación (1) y considerando 2 1 0
Z Z
y 2 2
2 1 2 0
V V g
por ser
el mismo diámetro en ambos puntos y por constituirse en un mismo nivel.
3
1 2 0 0 4.048[ ] 0.9 62.4[ ]
P P pies lb pie
3
1 2 2
1
227.34
12
lb pie
P P
pie pulg
⟹
2
1 2 1.579[ ]
P P lb pulg
P-6.7 De un depósito grande fluye agua a 10 ºC a una velocidad de 2 2
1.5 10 [ ]
m s
a
través del sistema que se muestra en la figura. Calcule la presión en B.
DATOS:
4" 97.97[ ]
D mm
,
6
1.5 10 [ ]
m
,
6 2
1.30 10 [ ]
v m s
Longitud equivalentes codo estándar
30
Le D
INCÓGNITAS:
PB=?
SOLUCION:
Sabiendo que la velocidad de flujo es:
/
/
/
/
/
/
/
1 /
/
A
.
-- ;.:_-=-- 1,5
m
I
1
/ 7,5 Tubo de
12m
m cobre de 4•
1 / tipo K
]
l=
/ ►
F:ujo
e ,J.
a
i
70m ►;
1
1
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-82-320.jpg)
![UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Guía Página 83
2 3
2
1.5 10 [ ]
2.0[ ]
(0.09797[ ]) 4
Q m s
V m s
A m
Empleando la ecuación de la energía en A y en B
2 2
2 2
2 2
A A B B
A L B
H O H O
P V P V
Z h Z
g g
Despejando de la ecuación de energía B
P y considerando 0
A
P
2
2 2
( )
2
A B
B A B L H O
V V
P Z Z h
g
(1)
Cálculo de L
h para el cual existen tres componentes:
1 2 3
L
h h h h
(2)
Donde:
2 2
1 1.0
2 2
B B
V V
h K
g g
Pérdida a la entrada
2 2 2
2
80.5[ ]
f f 821.68 f
2 0.09797[ ] 2 2
B B B
V V V
L m
h
D g m g g
Pérdida por fricción
2 2 2
3 T T T
f 3 f 30 3 90 f
2 2 2
B B B
V V V
Le
h
D g g g
Perdida por codos estándar
Sustituyendo las perdidas de energia en (2)
2 2 2
T
1.0 821.68 f 90 f
2 2 2
B B B
L
V V V
h
g g g
2
T
1.0 821.68 f 90 f
2
B
L
V
h
g
(3)
Cálculo de fT para un conducto de 2 pulg de cobre considerando completa
turbulencia
T
1
2log(3.7 )
f
D
⟹
2 2
T
1 1
f 0.0086
2log(3.7 ) 2log(3.7 65313)
D
Número de Reynolds:
5
5 2
0.09797[ ] 1.99[ ]
1.5 10
1.30 10 [ ]
R
DV m m s
N
v m s
/
✓ /
/
/ /
/
/
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-83-320.jpg)
![UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Guía Página 84
Rugosidad relativa:
[ ]
[ ]
Obteniendo f del diagrama de Moddy f 0.016
y reemplazando los valores en (3)
2
2
(2.0[ ])
1.0 821.68 0.0165 90 0.0085 3.126[ ]
2 9.81[ ]
L
m s
h m
m s
Sustituyendo valores en (1) se tiene B
P .
2
3
2
(2.0[ ])
(12[ ] 0[ ]) 3.126[ ] 9.81[ ]
2 9.81[ ]
B
m s
P m m m KN m
m s
3
(12 0.204 3.126)[ ] 9.81[ ]
B
P m KN m
⟹ 85.05[ ]
B
P KPa
P-6.8 Del sistema mostrado en la figura se bombeará keroseno ( 0.82
sg ) a 20ºC, del
tanque A al tanque B incrementando la presión en el tanque sellado A sobre keroseno. La
longitud total de la tubería de acero calibre 40 de 2 pulg. es de 38m, los codos son
estándar. Calcule la presión que se requiere en el tanque A para causar una velocidad de
flujo de 435L/min.
DATOS:
2" 52.50[ ]
D mm
,
5
4.6 10 [ ]
m
,
3
1.30 10 [ ]
v Pa s
Longitud equivalentes válvula
check 150
Le D
Longitud equivalentes válvula
de ángulo 150
Le D
SOLUCION:
Velocidad de flujo:
3
2
435[ min] 1[m ] 1000[ ] 1[min] 60[ ]
3.35[ ]
(0.0525[ ]) 4
Q l l s
V m s
A m
Empleando la ecuación de la energia en A y en B
2
2 2
2 2
A A B B
A L B
KER H O
P V P V
Z h Z
g g
Despejando de la ecuación de energía A
P y considerando 0
B
P
/
/
/
/
/
- B
/
/
/ /
/
.l
Flu10 1
va1vula
de Angulo
/
/
Valvula c:heck
tipo balanceo
/
Tubena de.acero
Cahbre '10 de 2·,
-- -
-- -
Tanque A
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-84-320.jpg)
![UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Guía Página 85
2 2
( )
2
B A
A B A L KER
V V
P Z Z h
g
(1)
Cálculo de L
h para el cual existen tres componentes:
1 2 3 4 5 6
L
h h h h h h h
(2)
Donde:
2 2
1 1.0
2 2
V V
h K
g g
Pérdida a la entrada
2 2
2 T T
f f 150
2 2
Le V V
h
D g g
Pérdida por válvula check
2 2
3 T T
f f 150
2 2
Le V V
h
D g g
Perdida por codos estándar
2 2
4 T T
f f 30
2 2
Le V V
h
D g g
Pérdida por codo estándar
2 2
5 1.0
2 2
B
V V
h K
g g
Pérdida por salida
2
2 2
6
38[ ]
f f 723.81 f
2 0.0525[ ] 2 2
B
V
L V m V
h
D g m g g
Perdida por fricción
Sustituyendo las pérdidas de energía en (2)
2 2 2 2 2 2
T T T
1.0 150 f 150 f 30 f 1.0 723.81 f
2 2 2 2 2 2
L
V V V V V V
h
g g g g g g
2
T T T
1.0 1 150 f 150 f 30 f 1 723.81 f
2
L
V
h
g
2
T
2 330 f 723.81 f
2
B
L
V
h
g
(3)
Se obtiene de la misma forma que el caso anterior f 0.019
T para un conducto de 2 pulg
de acero nuevo.
Número de Reynolds:
C
Rugosidad relativa:
[ ]
[ ]
Obteniendo f del diagrama de Moddy f 0.023
y reemplazando los valores en (3)
2
2
(3.35[ ])
2 330 0.019 723.81 0.023 14.253[ ]
2 9.81[ ]
L
m s
h m
m s
Sustituyendo valores en (1) y considerando
2 2
2 0
A B
V V g
se tiene A
P .
/
/
/
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-85-320.jpg)
![UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Guía Página 86
A
Válvula de globo
completamente
abierta
B
12 pies
Codo
3
4.5[ ] 0 14.253[ ] 0.82 9.79[ ]
A
P m m kN m
⟹
150.5[ ]
A
P KPa
P-6.9 El agua del tanque mostrado en la figura se va a hacer fluir hacia un drenaje.
Determine el tamaño de la tubería de acero Calibre 40 que transportará al menos 400
gal/min del agua a 80° F a través del sistema mostrado. La longitud total de tubería es de
75 pies.
Datos:
Q=400 gal/min
L=75 pie
v = 9,15*10-6
pies2
/s
= , * -4
pies
SOLUCION:
Empleando la ecuación de la energía en A y en B
Despejando la perdida de energía (hL) y considerando PA – PB/γ = VA = 0
[ ]
⁄
Donde los componentes de la perdida de energía son:
Donde:
/
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-86-320.jpg)
![UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Guía Página 87
Sustituyendo los componentes de la pérdida de energía en (2)
Sustituyendo (3) en (1) y despejando el factor f:
[ ] [ ]
Por continuidad
Sustituyendo (5) en (4)
Esta ecuación (6) se utilizará para iterar el diámetro D. Puesto que no
podemos despejar D en términos de f, la iteración se llevará a cabo como sigue:
Calculo del número de Reynolds en función del diámetro:
Calculo de la rugosidad relativa en función de D:
Procedimiento de Iteración
1. Asúmase el valor de D
2. Calcule f en la ecuación (6)
3. Calcule la rugosidad relativa (D/E) empleando la ecuación (8)
4. Calcule el numero de Reynolds empleando la ecuación (7)
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-87-320.jpg)


![UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Guía Página 91
En el diseño o análisis de un sistema de flujo de tubería existen seis parámetros básicos
involucrados, llamados:
1. Las pérdidas de energía del sistema o la adición de energía al sistema.
2. La velocidad de flujo de volumen del fluido o la velocidad del fluido.
3. El tamaño de la tubería.
4. La longitud de la tubería.
5. La rugosidad de la pared de la tubería, ε.
6. Las propiedades del fluido como peso específico, densidad y viscosidad.
Normalmente, se determinará uno de los parámetros mientras que los demás se conocen o
pueden especificarse por el diseñador. El método de llevar a cabo, el diseño o completar el
análisis es diferente dependiendo de lo que no se sabe. Los métodos que describimos en
este texto se clasifican de la siguiente manera:
Se determinarán las pérdidas o adiciones de energía.
Se determinará la velocidad del flujo de volumen.
Se determinará el diámetro de la tubería.
PROBLEMAS RESUELTOS
P-7.1 Según la figura mostrada calcular el caudal en litros/seg y la potencia de la bomba
en HP tomando en cuenta que la presión en el punto 2 es 175 KPa.
DATOS:
tramo Diámetro
(Pulg.)
Longitud
(m)
1-2 3 100
2-3 2 60
e=4.6*10-5
m
Vis osidad i e áti a υ= . * -6
[m2
/s]
INCÓGNITAS:
a) Q=?
b) Pott.=?
B
Figura
)
1
(
)
2
(
)
3
(
95
.
0
.
comp
val
k 80
.
0
tb
tk
k 00
.
1
tk
tb
k
64
.
0
º
90
codo
k
A
comp
val %
100
.
.
m
5
m
15
1 1 1 1
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-91-320.jpg)


![UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Guía Página 94
P-7.2 Se encuentra fluyendo agua a 40°C de A hacia B a través del sistema mostrado en la
figura. Determine la velocidad de flujo de volumen del agua si la distancia vertical entre las
superficies de los depósitos es de 10 m. Ambas tuberías son de hierro cubiertas de asfalto.
Los codos son estándar.
Encontrando los valores:
= , * -7
m2
/s
= , * -4
m
Longitud equivalente vál. Mariposa completamente abierta Le/D=340
Longitud equivalente de codo estándar de 90° Le/D=30
Asumiendo D6/D3= . la velo idad de flujo e el o du to de de , /s
encontramos K=0,45
SOLUCION:
Empleando la ecuación de energía en A y en B:
Despejando la pérdida de energía:
[ ]
Sustituyendo los valores y considerando PA-PB/γAGUA=0 y VA
2
- VB
2
/2g=0
hL = ……………………………………………………………………………………….... E .- 1)
Velocidad de flujo en ambos conductos:
Q6 = Q3 => A6*V6 = A3*V3
A
B
10m
Tubería de 5”
DI=165.2 mm
Longitud total=30m
Tubería de 3”
DI=90.9 mm
Longitud total=55m
Flujo
Alargamiento Repentino
Válvula de mariposa
completamente
abierta
-----
- - -
-----
- - -
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-94-320.jpg)
![UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Guía Página 95
V6
2
= (0.3028*V3)2 => V6
2
= 0.0917V3
2
…………………………………………... E .- 2)
Perdida de energía en el sistema para el cual existen 8 componentes:
hL = h1 + h2 + h3 + h4 + h5 + h6 + h7 + h8………………………………………….... (Ec.- 3)
Donde:
Perdida por fri ió , 6
(Perdida por salida)
Calculo de f3T y f6T, considerando completa turbulencia
[
⁄
] [ ]
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-95-320.jpg)
![UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Guía Página 96
[
⁄
] [ ]
Sustituyendo los componentes de la perdida de energía en (3) bajo una factorización de
la velocidad de ambos conductos.
………………….….. E .- 4)
Sustituyendo (1) y (2) en (4)
⁄
√
⁄
………………………………………………………………. E .- 5)
Nu ero de Rey olds e el o du to de :
⁄
…………………………….… E .- 6)
Rugosidad relativa o du to de :
Comienza el proceso de iteración como prueba inicial f3 = 0.023.
Nu ero de Rey olds e el o du to de 6 :
⁄
……………………………….………….. E .- 7)
Rugosidad relativa o du to de 6 :
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-96-320.jpg)



![UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Guía Página 100
por unidad de flujo en cada rama del sistema. Se puede demostrar escribiendo la ecuación
de energía utilizando los puntos 1 y 2 como puntos de referencia:
)
3
...(
..........
2
2
2
2
2
2
2
1
1
1
g
v
Z
P
h
g
v
Z
P
L
PROBLEMAS RESUELTOS
P-8.1 Un sistema de conducción de agua está constituido por tres tuberías que partiendo
del punto A convergen en el punto B. Las características de las tuberías son:
Tubería Longitud [m] Diámetro [in] e/D
1 1600 6 0.0003
2 1000 5 0.0004
3 800 4 0.0005
El caudal del agua a través del sistema es de 100 m3
/h. La presión en A y B es la atmosférica
y el nivel de A está situado 3 m por debajo del nivel de B. Determínese el caudal a través de
cada tubería y la potencia teórica de la bomba a instalar.
DATOS:
Q=100m3
/s
ZA=3m
INCOGNITAS:
Q1, Q2, Q3=?
Pott=?
1) Caudal supuesto a través de la tubería de 6”
2)
m
3
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-100-320.jpg)



![UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Guía Página 104
[ ]
P-8.3 Se encuentra fluyendo 100 gal/min de agua a 60 ºF en una tubería de acero Calibre
40 de 2 pulg. en la sección 1. El intercambiador de calor en la rama tiene un coeficiente
de pérdida de k=7.5 basado en la cabeza de velocidad de la tubería. Las tres válvulas están
abiertas completamente. La rama b es una línea de bypass compuesta de tubería de acero
Calibre 40 de 1 ¼ pulg. Los codos son estándar. La longitud de la tubería entre los puntos 1
y 2 en la rama b es de 20 pies. Debido al tamaño del intercambiador de calor, la longitud
de la tubería en la rama es muy corta, por lo que se pueden despreciar las pérdidas de
fricción. De este arreglo, determine:
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-104-320.jpg)

![UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Guía Página 106
Del diagrama de Moody una estimación lógica para el factor de fricción fb=0,023.
Sustituyendo este en la ecuación para hb obtenemos:
( ⁄ ) ( ⁄ )
Ahora tenemos:
⁄ ( ⁄ )
Despejando va obtenemos:
Entonces:
Después tenemos que:
⁄
[ ]
⁄
⁄
⁄
Puesto que realizamos estos cálculos utilizando un valor supuesto para fb, deberíamos
verificar la exactitud del supuesto.
Podemos evaluar el número de Reynolds para la rama b.
⁄
De tablas =1.21*10-5
pies2
/s. Entonces:
⁄
Utilizando este valor y la rugosidad relativa de 767 de ante, en el diagrama de Moody
obtenemos un nuevo valor para fb=0,25. Debido a que este valor es muy diferente del
valor supuesto de 0,023, podemos repetir los cálculos:
( ⁄ ) ( ⁄ )
⁄
Igualando las pérdidas de cabeza en las dos ramas:
⁄ ⁄
Despejando las velocidades:
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-106-320.jpg)
![UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Guía Página 107
Sustituyendo este valor en la ecuación de vb utilizada anteriormente obtenemos:
⁄
[ ]
⁄
⁄
⁄
Al volver a calcular el número de Reynolds para la rama b obtenemos:
⁄
⁄
No existe un cambio significativo en el valor de fb. Por lo tanto, los valores de las dos
velocidades calculadas anteriormente son correctos.
Ahora calculamos las velocidades de flujo de cabeza Qa y Qb:
⁄ ⁄
⁄ ⁄
Convirtiendo estos valores a las unidades de gal/min obtenemos Qa=74,5 gal/min y
Qb=25,5 gal/min
Para calcular la caída de presión, podemos escribir la ecuación de la energía utilizando los
puntos 1 y 2 como puntos de referencia. Puesto que las velocidades y elevaciones son las
mismas en estos puntos, la ecuación de la energía es:
Despejando la caída de presión obtenemos:
Puesto que hL1-2=ha=hb:
Entonces:
⁄ ⁄
Observe que esto no toma en cuenta las pérdidas secundarias. Entonces tenemos que:
⁄
⁄
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-107-320.jpg)

![UMSA-FACULTAD
DE
INGENIERIA
OPERACIONES
UNITARIAS
PET-245
Guía
Página
109
análogas
en
las
ecuaciones
anteriores;
Designando
por
Dh
a
l
suma
de
la
carga
de
presión
y
la
carga
de
altura
en
D,
tendremos:
El
problema
podemos
resolverlo
por
tanteo,
dando
un
valor
arbitrario
a
Dh
,
determinando
los
valores
de
las
cargas
de
fricción
para
este
valor
de
Dh
,
y
calculando
después
los
valores
de
1Q
,
2Q
y
3Q
,
según
el
método
indicado
en
el
ejemplo
1-8.
Si
tomamos
para
Dh
un
valor
menor
que
Dz
ha
de
cumplirse
que:
3 2 1
Q Q Q
[A]
En
caso
de
no
cumplirse
esta
igualdad,
si
resulta
menor
mayor
nos
indica
que
el
valor
tomado
para
Dh
es
alto
bajo
,
siendo
necesario
variar
el
valor
de
Dh
hasta
que
se
cumpla
la
igualdad
[A].
Si
tomamos
para
Dh
un
valor
mayor
que
Bz
,
ha
de
cumplirse
que:
3 2 1
Q Q Q
[B]
En
caso
de
no
cumplirse
esta
igualdad,
si
resulta
menor
mayor
nos
indica
que
el
valor
tomado
para
Dh
es
alto
bajo
,
siendo
necesario
variar
el
valor
de
Dh
hasta
que
se
cumpla
la
igualdad
[B].
1
er
tanteo:
valor
supuesto
para
Dh
=5m
Ramificación
AD
5
1
1
4
10*53.1 34260
800
3.0*81.9*2
10*7
870*3.0
Re
f
f
h
h
f
00016.0
D
5.8
1
f
seg m h
f
u
f
/ 30.3 *0867.0
1
1 1
h m Q
/ 820
3
1
Ramificación
BD
4
10*66.7 Re
f
00016.0
D
3
2
1
f D
f D B
f D A
h h
h h z
h h z
J
I
_J
J _J
_J
I
t _J
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-109-320.jpg)


![UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Guía Página 112
P-9.2 Para el sistema de tres ramas que se muestra en la figura, determine la distribución
de flujo de Qi de agua y la carga piezometrica H en la unión. El aporte de potencia al fluido
po pa te de la o a es o sta te, e igual a γQHp= kW. “upo ga fa to es de fricción
constantes.
Tubo L [m] D [m] f ∑K
1 50 0.15 0.020 2
2 100 0.10 0.015 2
3 300 0.10 0.025 1
SOLUCION:
Los equivalentes de los coeficientes de resistencia se calculan de la siguiente forma:
Considerando:
Se tiene:
Suponiendo las direcciones de flujo que se indican. La ecuación de energía para el tubo 1
desde el depósito hasta la unión B es:
Donde H es la carga piezometrica en B. Sustituyendo los parámetros conocidos y
despejando H se obtiene:
Figura
m
alt 20
m
alt 5
m
alt 13
2
3
1
P
B
m
x
Le 15
2
02
.
0
15
.
0
1
m
x
Le 7
.
6
1
015
.
0
10
.
0
2
m
x
Le 4
1
025
.
0
10
.
0
3
5
2
3
5
2
1 /
10
42
.
1
15
.
0
81
.
9
65
02
.
0
8
m
s
x
x
x
x
x
R
5
2
4
5
2
2 /
10
32
.
1
10
.
0
81
.
9
7
.
106
015
.
0
8
m
s
x
x
x
x
x
R
5
2
4
5
2
3 /
10
28
.
6
10
.
0
81
.
9
304
025
.
0
8
m
s
x
x
x
x
x
R
5
2
2
2
2
2
8
4
2
D
x
x
g
L
x
f
x
D
x
v
g
v
D
L
x
f
Q
h
R L
i
2
1
1
1 Q
R
H
H
Z P
2
1
3
1
3
10
42
.
1
9800
10
20
10 Q
x
Q
x
H
2
1
1
1420
4
.
2
10 Q
Q
H
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-112-320.jpg)

![UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Guía Página 114
CAPITULO 10
FLUJO DE FLUIDO“ COMPRE“IBLE“
En los ejemplos indicados anteriormente hemos hecho aplicación de la Ec. de energía
considerando los fluidos incompresibles; en el caso de flujo de gases no podemos hacer esa
suposición, para la deducción de una ecuación aplicable para estos casos podemos partir de la Ec.
de energia, que escrita en forma diferencial (suponiendo que el flujo es horizontal y que no realiza
trabajo ni se le suministra calor), se convierte en:
0
2
2
gD
dL
u
f
dp
g
udu
Esta ecuación no puede integrarse directamente debido a que la velocidad u varia al variar p, que
a su vez es función de la longitud L.
Es conveniente poner la ecuación anterior en función de la velocidad másica G, que es la misma en
cualquier punto de la canalización. Tendremos en cuenta las relaciones que indicamos
seguidamente para su sustitución en la ecuación anterior:
1
0
2
,
,
2
2
D
dL
g
V
G
f
V
dp
g
g
g
GdV
GV
Gdv
du
A
W
G
u
u
V
u
G
c
Dividiendo por V2
2
0
2
2
2
D
dL
g
G
f
V
dp
g
g
V
dV
g
G c
Para integrar esta expresión es necesario tener en cuenta que f es función del Re = DG/μ, que es
independiente de la densidad del fluido, pero que depende de la viscosidad del mismo. De todos
modos, la variación de f con la viscosidad es pequeña, y prácticamente podemos tomar la media
aritmética de los valores correspondientes a las condiciones extremas:
2
2
1 f
f
f
Y considerar este valor constante para efectos de integración. En tales condiciones la integración
de la Ec. [1-27] entre los estados 1 y 2 nos lleva a:
3
0
2
ln
2
2
1
1
2
2
D
L
g
G
f
V
dp
g
g
V
V
g
G c
Flujo isotermo de un gas ideal.- En este caso particular
4
2
1
1
1
2
1
2
2
2
1
1
1
2
1
V
p
p
p
dp
p
V
p
V
dp
Y
2
1
1
2
p
p
V
V
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-114-320.jpg)
![UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Guía Página 115
Luego
5
0
2
2
ln
2
1
1
2
1
2
2
2
1
2
D
L
g
G
f
V
p
p
p
g
g
p
p
g
G c
Si designamos por Vm el volumen especifico a la presión media, podemos escribir:
1
1
2
1
2
V
p
V
p
p
m
Y
6
1
2
2
1
2
1
1
1
2
1
2
1
1
2
1
2
2
p
p
V
V
p
p
p
p
p
V
p
p
p
m
Entonces
7
0
2
ln
2
1
2
2
1
2
D
L
g
G
f
V
p
p
g
g
p
p
g
G
m
c
Si la caída de presión a lo largo de la canalización es pequeña en relación con la presión
total, el primer termino de la Ec. [1-32], que representa el aumento de la energía cinética
del fluido, será pequeño y despreciable frente a los otros dos, y en tales condiciones
8
0
2
2
1
2
D
L
g
G
f
V
P
P
c
m
Y de aquí:
D
L
g
G
f
V
P
P
c
m
2
*
2
1
2
9
2
1
2
1
*
2
2
2
D
L
u
g
f
D
L
V
u
g
f
V m
m
m
m
c
m
Siendo um y γm la viscosidad y el peso especifico del fluido a la presión media de p1 y p2.
Donde:
P1= Presión de entrada a la tubería
P2= Presión de salida de la tubería
Vm= [1/γm] Volumen especifico promedio a Pm (P1+P2/2)
γm= Peso especifico promedio a Pm (P1+P2/2)
f= factor de fricción
L= Longitud de la tubería
D= Diámetro interno de la tubería
G=Gasto
R= Constante universal de los gases
M= Peso molecular del gas
ρ= Densidad
v= Velocidad
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-115-320.jpg)
![UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Guía Página 116
PROBLEMAS RESUELTOS
P-10.1 Desde una instalación productora de acetileno hasta el lugar de ampliación situado
a 5000 [ ] se transporta este a razón de100 [ ] (Medidos en condiciones normales) por
una tubería de hierro de 5´´. Determine ser la presión a que se encuentra el acetileno
cuando entra en la tubería si en el lugar de aplicación (a la salida de la tubería) ha de
encontrarse a 1 [ ] de presión.
El flujo del acetileno a través de la tubería es isotermo a 25
(La densidad del acetileno a 0 y 1 [ ] es 1.1708 [ ], y su viscosidad a 25 Es
poises. Las características de la tubería se dan en la tabla a-19.)
SOLUCIÓN:
[ ]
Haciendo uso de la Ec.
[ ] [ ]
A continuación se determina el valor de correspondiente a la presión media,
efectuándose el cálculo por tanteo:
1er. Tanteo: presión supuesta, [ ]
[ ]
[ ]
m
g
G
D
L
f
P
P
*
2
*
2
2
1
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-116-320.jpg)
![UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Guía Página 117
2do. Tanteo: presión supuesta, [ ]
[ ]
[ ]
3er. Tanteo: presión supuesta, [ ]
[ ]
[ ]
Como resultado encontramos que la presión a que ha de entrar en la tubería ha de ser
11,80[ ].
P-10.2 Por tubería de hierro de 3 ´´ circula una corriente de hidrógeno con un caudal de
500 , medido a 0 y 1 [ ]. La longitud total de la tubería, incluidos los accesorios,
es de 400 [ ] Y la presión de entrada del hidrógeno en la tubería es de 30 [ ].
Determine ser la presión de salida si el flujo es isotérmico a 20 .
El factor de compresibilidad para el hidrógeno a 20 . En función de la presión es el
indicado en la tabla siguiente.
Presión Atm z
1 1.0732
10 1.0791
20 1.0855
30 1.0920
40 1.0985
La viscosidad puede suponerse invariable con la presión, y a 20 . Vale 0.009 cent poises.
La densidad a 0 y 1 Atm. es 0.0898 [ ].
SOLUCIÓN:
A partir de la Ec. [7] despreciando el primer término y haciendo , tenemos:
En las condiciones del problema:
[ ] [ ]
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-117-320.jpg)
![UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Guía Página 118
Sustituyendo en Ec. [1-35]
[ ] [ ]
Por tanto, la presión vendrá dada por:
La resolución de esta ecuación la efectuaremos por tanteo:
1er. Tanteo: presión supuesta, [ ]
[ ]
1er. Tanteo: presión supuesta, [ ]
[ ]
La presión debida es de 24 [ ] O sea que la pérdida de presión por fricción a lo largo de
la tubería es de 6 [ ]
En realidad, podíamos haber resuelto el problema admitiendo que el hidrógeno se
comporta como gas perfecto en este intervalo de presiones, ya que aproximadamente es
así, podemos observar en la pequeña diferencia del factor de compresibilidad respecto a
la unidad para el intervalo de presiones que hemos considerado.
P-10.3 De llevarse aire a 25 Por una tubería de 3´´ a lo largo de una conducción de 2000
[ ] De longitud total.
El aire entra en la tubería a 2 [ ] De sobrepresión, y se desea conocer la presión de
salida si en el lugar de aplicación se necesitan 1000 [ ] (Las características del tubo y del
fluido se dan en tablas)
SOLUCIÓN:
Teniendo en cuenta que el fluido es isotérmico y suponiendo que el gas se comporta como
ideal, haremos uso de la Ec. [7], calculando, en primer lugar, el último término de esta
ecuación, que es correspondiente a la fricción.
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-118-320.jpg)
![UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Guía Página 119
En las condiciones del problema:
[ ] [ ]
El término correspondiente a la fricción valdrá:
[ ]
La primera aproximación podemos escribir el término cinético quedando entonces:
[ ]
Que podemos poner de la forma:
̅
Siendo ̅
̅ La presión media entre resolviendo la ecuación anterior por tanteo
tenemos:
P supuesta [Atm] P calculada [Atm]
2 2.85
2.85 2.44
2.50 2.58
256 2.56
Con esta presión calculada determinaremos ahora el valor del término cinético.
( )
Observamos que éste término resulta casi despreciable frente al correspondiente al de la
fricción, siendo innecesario efectuar corrección alguna para el valor de este término que
no hemos tenido en cuenta en primera aproximación.
Si este término resultara significativo, sería necesario incluirlo al efectuar el cálculo por
tanteo. En general, suele ser despreciable, y su supresión facilita los cálculos.
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-119-320.jpg)


![UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Guía Página 122
seg
m
u 406
,
1
3
seg
m
u 247
,
1
4
seg
m
u 994
,
0
5
La velocidad media correspondiente a estos cinco valores es
seg
m
u 367
,
1
El caudal será
h
m
seg
m
Q 3
3
2
187
052
,
0
11
,
0
*
*
367
,
1
h
m
Q 3
187
b) 5
3
10
*
31
,
2
10
*
3
,
1
1000
*
22
,
0
*
367
,
1
e
R
81
,
0
máx
u
u
seg
m
umáx 688
,
1
145
,
0
2
2
g
u
hK
mm
h 242
6
,
0
10
*
145
,
0 3
Tiempo de descarga.- Cuando un depósito en el que esta contenido un líquido se está
descargando, desciende el nivel del líquido en el mismo; la velocidad de salida disminuirá
a medida que va descendiendo el nivel del líquido, y por tanto el tiempo de descarga de
un volumen determinado de líquido dependerá de aquel nivel. En el ejemplo siguiente
hacemos un estudio de este problema.
P-11.2 Un deposito cilíndrico de 1 m de diámetro y 4m de altura está lleno de agua a 200
C.
Perpendicularmente al fondo del depósito esta conectando un tubo de 1.5´´ y 5 m de
longitud a través del cual de vacía. Calcúlese el tiempo que tarda en descender 1 m el nivel
de agua en el depósito.
SOLUCIÓN:
Considerando un punto del depósito a una altura z, al descender al nivel dz en el tiempo
dt, el caudal vendrá dado por:
dt
dz
A
Q dep [A]
En este instante, a través del tubo de sección A2, circulara el mismo caudal
Q = A2 u2 [B]
/
/
/
/
/
/
/ /
~-;¡
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-122-320.jpg)
![UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Guía Página 123
Podemos considerar que la velocidad u1 del agua dentro del depósito es despreciable
frente a la velocidad u2 en el tubo. Si tomamos como plano de referencia para alturas el
punto inferior del tubo (z2 = 0), la aplicación de la Ec. de energía nos conduce a la
expresión:
D
fL
gz
u
h
z
g
u
f
/
1
2
;
0
2
2
1
2
2
Igualando las expresiones [A] y [B], una vez sustituido el valor de u2 en [B], tendremos:
1
2
/
1
2
2
/
1
/
1
2
2
1
2
1
2
1
2
1
final
inicial z
z
g
D
fL
A
A
t
dz
z
g
D
fL
A
A
dt
D
fL
gz
A
dt
dz
A
Para efectuar la integración hemos supuesto que f es constante; en realidad no ocurre
esto y debemos operar con un valor medio adecuado, cuyo cálculo se verifica del modo
siguiente:
Cuando empieza a descargarse el depósito (z = 9)
)
10
*
9
.
40
/(
1
9
*
8
.
9
*
2
3
2
fL
u
La longitud total serán los 5 m de tubería más la longitud equivalente al estrechamiento
brusco, que vale 0.6 m; por lo tanto L = 5.6 m y:
f
u
137
1
3
.
13
2
El valor de f lo determinaremos por tanteo:
1.er
tanteo: Suponemos u2 = 10 m/seg.
Re = 4.08*105
ε/D = .
f = 0.0205
u2 = 6.81 m/seg.
2. ° tanteo: Suponemos u2 = 6.81 m/seg.
Re = 2.78*105
f = 0.0212
u2 = 6.73 m/seg.
3. ° tanteo: suponemos u2 = 6.73 m/seg.
Re = 2.75*105
f = 0.0212
u2 = 6.73 m/seg.
En consecuencia, el valor de f al principio de la operación es:
f = 0.0212
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-123-320.jpg)



![Aux. José Luis Huanca P.
UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Guía Página 127
12.4 DIAGRAMAS DE PRESIÓN DE VAPOR.
En esos diagramas se representan las composiciones de las mezclas frente a la presión
parcial de vapor de cada componente, a una temperatura determinada. Se representa
también en dichos diagramas la presión total como suma de las presiones parciales
ejercidas por amos componentes.
12.5 DIAGRAMAS DE EQUILIBRIO.
En estos diagramas se representan las composiciones del líquido frente a las del vapor en
equilibrio, a presión total constante.
12.6 LEY DE RAOULT.
Cuando se trata de disoluciones ideales se pueden determinar los datos para la
construcción de los diagramas anteriores a partir de las tensiones de vapor de los
componentes puros. Este comportamiento ideal se representa en mezclas cuyos
constituyentes muestran gran semejanza química, y se aproximan a este comportamiento
las mezclas cuyos componentes tienen iguales presiones críticas. Estas disoluciones
obedecen a la ley de Rault, según la cual <<la presión de vapor de cada componente es
igual al producto de la fracción molar de dicho componente en la fase líquida por la
tensión de vapor del componente puro a la misma temperatura>>:
[1]
( ) ( ) [2]
Si la mezcla cumple con la ley de Dalton ( ) la presión necesaria para que la
mezcla hierva será:
( ) [3]
Por otra parte, como la fracción molar en la fase de vapor es la relación entre la presión
parcial y la presión total, tendremos:
⁄ [4]
⁄ [5]
12.7 VOLATILIDAD RELATIVA.
se denomina volatilidad de un componente en una mezcla a la relación entre su presión
parcial de vapor y su concentración en la fase líquida, es decir:
Volatilidad de A = pA/xA [6]
Volatilidad de B = pB/xB [7]
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-127-320.jpg)
![Aux. José Luis Huanca P.
UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Guía Página 128
Al cociente entre las volatilidades de componente más volátil y del menos volátil se
denomina volatilidad relativa, α; es decir:
⁄
⁄
[8]
( ⁄ )
⁄ [9]
Como y , podemos deducir la expresión:
( )
[10]
En términos estrictos, la volatilidad relativa es función de la temperatura, sin embargo,
para algunas mezclas permanece prácticamente constante en el intervalo normal de
operación.
EJEMPLO.1 Las tensiones de vapor del heptano y el octano son las siguientes:
t, o
C P7 P8 t, o
C P7 P8
98,4
100
102
104
106
108
110
112
760
795
841
890
941
993
1049
1104
377
356
380
406
429
452
479
510
114
116
118
120
122
124
125,6
1165
1228
1296
1368
1442
1528
1593
540
574
609
647
687
729
760
Si las mezclas de estos componentes cumplen la ley de Rault
Determínese:
a) Los datos de equilibrio para este sistema a la presión de una atmosfera calculados
directamente a partir de las presiones de vapor.
b) La volatilidad relativa a cada temperatura.
c) La relación analítica entre las composiciones de equilibrio de la mezcla a la presión
de una atmosfera, tomando el valor medio de la volatilidad relativa.
SOLUCIÓN:
A 124o
C, haciendo uso de las Ecs. [3] Y [4]:
760=1528X + 729(1-X)
X=0,0388
Y=1528X/760 = 0,0778
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-128-320.jpg)
![Aux. José Luis Huanca P.
UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Guía Página 129
A 122O
C
760 = 1442x + 687 (1-x)
x = 0,0967
y = 1442x/760 = 0,1835
A 120O
C
760 = 1368x + 647(1-x)
x = 0,1563
y = 1368x/760 = 0,2821
Operando del mismo modo para otras temperaturas se obtienen los datos que
resumimos en la tabla siguiente:
t, o
C x y α t, o
C x y α
125,6
124
122
120
118
116
114
112
0,000
0,039
0,097
0,156
0,220
0,284
0,352
0,421
0,000
0,078
0,184
0,282
0,375
0,450
0,541
0,613
2,096
2,096
2,099
2,114
2,128
2,139
2,157
2,165
110
108
106
104
102
100
98,4
0,495
0,569
0,647
0,733
0,824
0,922
1,000
0,681
0,743
0,801
0,862
0,912
0,963
1,000
2,190
2,197
2,193
2,192
2,213
2,233
2,255
b) Las volatilidades relativas para cada temperatura, incluidas en la tabla anterior, se han
de terminado por el cociente entre las tenciones de vapor de los componentes puros.
c) El vapor medio aritmético de la volatilidad relativa para todo el intervalo es igual a
α = 2,17
Entonces la relación analítica entre las concentraciones de equilibrio
Resulta (Ec. [10]):
Y =
12.8 DESVIACIONES DE LA IDEALIDAD.
para la mayor parte de las mezclas. La presión total obtenida para una temperatura
determinada es Distinta De la prevista por la ley de rault, Ecs. [3], y decimos que Estas
mezclas presentan desviaciones de la idealidad, siendo mucho más abundantes las
mezclas las con desviaciones positivas (cuando la Presión total es mayor que la prevista
por la ley de Rault) que con desviaciones negativas.
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-129-320.jpg)
![Aux. José Luis Huanca P.
UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Guía Página 130
Sin embargo cuando la concentración de un componente, expresada en fracción molar, se
aproxima a la unidad, su comportamiento se aproxima al previsto por la ley de Rault; por
tanto, en disoluciones muy concentradas , e8sta le8y se puede aplicar como limite al
componente que se halla en mayor proporción.
Si se trata de disoluciones diluidas, y para el componente que se Encuentra en menor
proporción, se puede aplicar la ley de Henry, Según la cual la presión de un componente
en el vapor es proporcional
A su conce8ntracion:
PA = CxA
Comparando el intervalo de aplicabilidad de estas dos leyes podemos Decir que la ley de
Rault es aplicable al disolvente, y la de Henry es aplicable Al soluto.
Las desviaciones del comportamiento ideal pueden tratarse introduciendo
Un coeficiente de corrección en las Ecs. [4] Y [5] de tal manera que
yA= [11]
yB= . [12]
Los coeficientes de corrección , denominados coeficientes de actividad, varían
con la concentración, siendo mayores que la unidad para las mezclas con desviaciones
positivas (log y > 0) y menores que la unidad para las mezclas con desviaciones negativas
(log y < 0); en cualquier caso, su valor se aproxima a la Unidad al hacerlo la fracción molar
del componente considerado.
12.9 MEZCLAS AZEOTROPICAS.
cuando las desviaciones de la ley de rault son suficientemente grandes, las mezclas
pueden presentar un máximo o un mínimo para la presión total en la curva presión de
vapor composición , correspondiendo este máximo o mínimo a la composición del
zoótropo son más abundantes las mezclas que presentan el máximo en la presión de
vapor que corresponde a un mínimo en la temperatura de ebullición , y en este caso
decimos que la mezcla presenta un zoótropo mínimo cuya composición corresponde al
mínimo que aparece en la curva de ebullición par una presión total determinada en estas
mezclas, las curvas de composición del liquido y del vapor son tangentes en el punto de
azeotropismo.
Las mezclas cuyo concentración es menor que la correspondiente al zoótropo, dan lugar
en ebullición a un vapor más rico en componente más volátil que el liquido de partida,
mientras que las mezclas de concentración superior a aquella dan un vapor mas pobre en
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-130-320.jpg)
![Aux. José Luis Huanca P.
UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Guía Página 131
componente más volátil que el liquido de partida .naturalmente, si se trata de una mezcla
cuya composición sea la del zoótropo dará lugar a un vapor de la misma composición
, comportándose como si se tratara de un componente puro; por tanto las mezclas de esta
composición no pueden separarse por destilación.
Para las mezclas que presentan un zoótropo máximo puede hacerse un razonamiento
análogo.
A partir de las Ecs. [5-11] Y [5-12], y teniendo en cuenta que para la composición del
azeotropo
YA=XA e YB=XB , podemos deducir la expresión.
= [13]
Por otra parte, como en las mezclas con desviaciones positivas (Mínimo en el punto de
ebullición) al aumentar la concentración del componente mas volátil aumenta el valor de
YB/YA , podemos deducir que para que se forme un azeotropo mínimo es condición
necesaria que el coeficiente de actividad del componente menos volátil llegue a ser mayor
que el cociente entre las tenciones de vapor del componente más volátil y del menos
volátil. Por un razonamiento análogo, deducimos que la formación de un azeotropo
máximo está condicionada a que el coeficiente de actividad del componente mas volátil
llegue a ser menor que la inversa de aquel cociente.
12.10 DESTILACION SIMPLE.
La destilación simple consiste en la vaporización parcial de una mezcla con producción de
vapor más rico en componentes más volátiles que la mezcla liquida inicial, quedando un
residuo liquido más rico en componentes menos volátiles se puede llevar de dos maneras:
12.10.1 DESTILACION DE EQUILIBRIO O CERRADA
En este caso el líquido se lleva a una temperatura intermedia entre la de principio y fin de
ebullición, dejando que la fase vapor formada alcance el equilibrio con la fase liquida, a
aquella temperatura.
Por aplicación de un balance de materia aplicado a todo el sistema
y al componente más volátil, llegamos a la expresión
= [14]
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-131-320.jpg)
![Aux. José Luis Huanca P.
UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Guía Página 132
que nos da la relación entre la cantidad de liquido residual L y la cantidad de vapor
separado V , en función de la composición inicial del liquido Xo, y las composiciones del
liquido y vapor en equilibrio a la temperatura y presión dadas x e y.
Sobre el diagrama de ebullición, construido a la presión de operación se leen
directamente las composiciones del líquido y del vapor en equilibrio, en función de la
composición del líquido inicial y de la temperatura de trabajo.
EJEMPLO.2 Una mezcla liquida de hexano y benceno que contiene 40 % en moles de
hexano, se somete a destilación cerrada a la presión atmosférica y temperatura constante
hasta que el 40 % del líquido inicial pasa a la fase vapor. Determínese la temperatura a
que ha de realizarse la operación y las condiciones del líquido residual y del vapor
separado.
Los datos de equilibrio para el hexano-benceno a 1 atm son los siguientes (expresadas las
composiciones en fracción molar):
x y T, ºC x y T, ºC
0.00 0.00 80.1 0.55 0.640 70.6
0.05 0.111 78.5 0.60 0.676 70.3
0.10 0.191 77.1 0.65 0.710 69.9
0.15 0.258 76.0 0.70 0.744 69.5
0.20 0.317 75.1 0.75 0.782 69.3
0.25 0.371 74.4 0.80 0.822 69.1
0.30 0.422 73.7 0.85 0.862 68.9
0.35 0.470 72.7 0.90 0.906 68.8
0.40 0.518 72.2 0.95 0.952 68.7
0.45 0.563 71.5 0.97 0.971 68.7
0.50 0.602 71.0 1.00 1.000 68.7
SOLUCIÓN:
A partir de los datos anteriores construimos el diagrama de ebullición (Fig. 2)
De acuerdo con la Ec.[5-14] y tomando como base de cálculo 100 moles de mezcla inicial,
tendremos:
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-132-320.jpg)

![Aux. José Luis Huanca P.
UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Guía Página 134
Podriamos tambien resolver este problema haciendo uso del diagrama de eqilibrio como
indicamos mas adelante.
En la practica la destilacion de equilibrio solo se aplica al tratamiento de petroleos,
haciendo pasar la mezcla de modo continuo y a presion a lo largo de un cambiador de
calor, que puede estar constituido por una serie de tubos calentados exteriormente, y se
descarga por una valvula de reduccion de presion a un recinto separador, tipo ciclon, en el
cual se separa la mezcla del liquido y el vapor en equilibrio (Figura siguiente); el liquido se
descarga por la parte inferior y el vapor que sale por la parte superior se lleva hasta un
condensador.
De la Ec.[14] deducimos para la relacion entre las concentraciones del vapor y del liquido
en equilibrio la expresion
[ ]
Sobre el diagrama de equilibrio esta ecuacion representa una recta de pendiente -(L/V)
que pasa por el punto (x0 , x0 ) de
82
80
78
76
74
72
~
~"'~
"" ~
~
................... · · · ; ~ .
--~
.................... ·····-··· ........
~ ~
70
-- -
68
o 0,2 0,4 0,6 0,8 1
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-134-320.jpg)


![Aux. José Luis Huanca P.
UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Guía Página 137
Siendo CLA y CLB los calores específicos de los componentes A y B en estado
liquido, y ∆Hm el calor de la mezcla.
Tomando valores medios para los calores específicos de ambos componentes nos
queda la expresión:
( ) ( ) ( ) (18)
b) Si se trata de una mezcla gaseosa de los componentes A y B a una temperatura
determinada, el cálculo de la entalpia de la mezcla se puede efectuar considerando
que su formación se realiza por el camino siguiente:
1) Calentamiento de los componentes puros desde una temperatura origen to
hasta la temperatura de ebullición del componente respectivo.
2) Vaporización de cada componente a su temperatura de ebullición.
3) Calentamiento de los vapores de los componentes puros desde su temperatura
de ebullición hasta la temperatura final de la mezcla.
4) Mezcla de los vapores.
La entalpia de la mezcla vendrá dada por la expresión:
[∫ ∫ ] ( ) [∫
∫ ] (19)
Siendo:
CLA y CLB = calores específicos de los componentes líquidos puros.
CVA y CVB = calores específicos de los componentes puros en estado de vapor.
λA y λB = calores latentes, a su temperatura de ebullición.
∆Hm = calor de mezcla en fase vapor.
Tomando los calores de vaporización de los componentes puros de la temperatura
final de la mezcla, la ecuación anterior se puede escribir en la forma:
[∫ ] ( ) [∫ ] (20)
Tomando valores de medio para los calores específicos, la expresión se transforma
en:
[ ( ) ] ( )[ ( ) ] (21)
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-137-320.jpg)


![Aux. José Luis Huanca P.
UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Guía Página 140
Teniendo en cuenta la Ec. (18) y considerando que el calor de mezcla es nulo por tratarse
de disoluciones de comportamiento ideal, la entalpia de la mezcla liquida resultante a
93.3ºC (tomando como temperatura origen de entalpias 30ºC), será
( ) ( )
A 93.3ºC los calores de vaporización de los componentes son
Benceno λB = 0.43 Kcal/Kg
Tolueno λT = 0.46 Kcal/Kg
De acuerdo a la Ec. (21) la entalpia del vapor resultante será
[ ( ) ] [ ( ) ]
La cantidad de calor que hay que suministrar a los 100 moles que hemos tomado como
base de calculo se determina haciendo uso de la Ec. (5-16):
1
t 0,8
'i 1 0.680 ...............................
0,6
0,4
0,2
•
o 1
0.46
o 0,2 0,4
1
O.SS
0,6 0,8 1
X
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-140-320.jpg)

![Aux. José Luis Huanca P.
UMSA-FACULTAD DE INGENIERIA OPERACIONES UNITARIAS PET-245
Guía Página 142
b) Si en el intervalo de operación la relación entre las composiciones de equilibrio
viene dada por la ecuación de una recta de la forma: , la Ec. (5-24) se
convierte en
( )
( )
(27)
En el caso en que la relación e y se encuentre tabulada, el valor de la integral indicada
en la Ec. (24) se determina gráficamente, representando la función ( )
⁄ frente a x, y
calculando el área comprendida entre la curva, el eje de abscisas y las ordenadas
extremas.
PROBLEMAS RESUELTOS
DESTILACIÓN CERRADA
P-12.1 Una mezcla de heptano y octano de composición 0.65 en fracción molar de
heptano, se somete a destilación cerrada a temperatura constante de 105ºC y presión
constante de 700 mmHg. Determínese:
a) Las composiciones del líquido y del vapor en el equilibrio.
b) El numero de moles que quedan en la caldera y los que pasan al estado vapor.
Las presiones de vapor del heptano y del octano a 105ºC son 915 mmHg y 417 mmHg.
Respectivamente.
SOLUCIÓN:
a) Determínese las composiciones de equilibrio por aplicación de la ley de Raoult:
b) De acuerdo con la Ec. [14]:
Tomando como base de cálculo 100 moles de mezcla inicial
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-142-320.jpg)






![Aux.
José
Luis
Huanca
P.
UMSA-FACULTAD
DE
INGENIERIA
OPERACIONES
UNITARIAS
PET-245
Guía
Página
149
A
V:
Ya
=?
Yb
=?
Yc
=?
B
C
L:
Xa
=?
Xb=?
Xc
=?
Sea:
Benceno
A
Xoa
=
0.5
Datos:
Pt
=
760
mmHg
V
=
49%
Tolueno
B
Xob
=
0.25
O
–
Xileno
C
Xoc
=
0.25
a)
Se
tendrá
que
calcular
las
temperaturas
de
ebullición
para
conocer
el
rango
de
la
temperatura
a
tantear.
b)
Sabemos:
∑
∑
(
∑
)
donde:
Ki
=
……
(1)
1
=
∑
(
)
(
)
(
)
…….
(
)
Además
por
Antonie:
Pvº
=
(
)
…..
(2)
Reemplazando
1
y
2
en
con
sus
respectivos
valores:
1
=
[
(
)
]
+
[
(
)
]
+
[
(
)
]
Donde:
A,
B,
C,
D,
E,
F,
X,
Y,
Z
son
constantes
de
Antonie.
Buscando
un
valor
de
“T”
para
la
igualdad
a
1
se
tiene:
T
=
103.36
(Cº)
“Temperatura
de
destilación”
El
resultado
anterior
es
aceptable
porque
se
encuentra
en
el
siguiente
rango:
Teb
“A”
=
80.1
(Cº)
Teb
“B”
=
110.62
(Cº)
Teb
“C”
=
144.41
(Cº)
a)
Por
Antonie:
Pv
=
(
)
Paº
=
1477083
mmHg
Pbº
=
615.37
mmHg
Pcº
=
222.64
mmHg
n
l
r A /'
'
A
'
'----------- ---~)
y
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-149-320.jpg)


![UMSA-FACULTAD DE lNGENIERIA OPERACIONES UNITARIAS PET-245
PROBLEMAS RESUELTOS
P-13.1 En una columna de rectificación en marcha continua, se destila una mezcla líquida
Cloroformo-Benceno de composición 55% MOLAR EN CHCL3, se desea obtener un
producto destilado de composición 94% molar y un residuo con 8% molar si la
alimentación entra en forma de vapor saturado, determine:
a) Los flujos de destilado y residuo
b) El reflujo mínimo
c) El nro. de bandejas, para una relación de reflujo de 30% superior a la mínima.
d) La posición de la bandeja de alimentación
e) El nro. mínimo de bandejas teóricas. Utilice el método Mcabe-Thiele.
DATOS:
P=760mmHg
CHCL3 -+ A
C6H6 -+ B
---+----i._--.-__;+ 1D}X D 1
Xp =0.55
Xn =0.94
X H = 0.08
F =1Oünioles
SOLUCION:
COMPUESTO A B
A 6.9371 1171.2
B 6.90565 1211.033
A B
-8
T = - - - - C.....(])
J
og Pv -A
Pv= IO r+c .....(2)
a) Los Flujos de Destilado y Residuo.
F=D + R (1)
Xp · F = XD · D + XR · R (2)
(1) En (2):
xF ·F = x0 ·D+xR ·R-xR · D
D = 0.55-100-0.08-100
0.94-0.08
D =54.65111.oles
,;r en (1)
<
Gula
R =45.35111.0~
<
Aux. José Luis Huanca P.
e Teb·e Ec. (1)
227 61.74
220.79 80.09
_ PvA
Y - p .....(4)
T
Página 151
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-152-320.jpg)

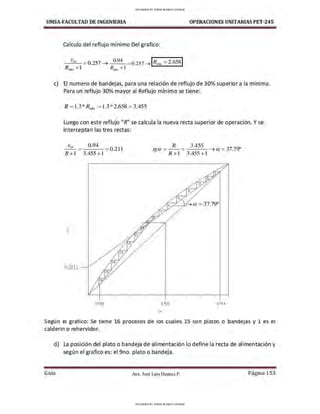
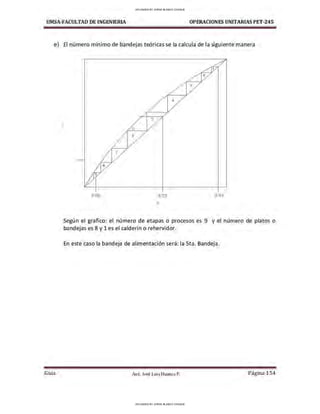
![UMSA-FACULTAD DE lNGENIERIA OPERACIONES UNITARIAS PET-245
P-13. A 500 mmHg de presión se destila una mezcla liquida con 40% molar de Benceno y
60% molar de Tolueno para producir 96% molar de Benceno y 96% molar de Tolueno
considerando un comportamiento ideal determinar a) El reflujo mínimo si la alimentación
se introduce a 702C b)EI numero de etapas en cada caso, para un reflujo R=l .8Rminimo c)
El número mínimo de bandejas.
DATOS:
P=500mmHg
BENCENO
TOLUENO
-+ A
-+ B
XF =0.40
XD =0.96
XR = 0.04
SOLUCION:
F
a) El reflujo mínimo si la alimentación se introduce a 702C
COMPUESTO A B e
A 6.90565 1211.033 220.790
B 6.95464 1344.800 219.482
T [2C] PvA Pve XiA
67,14 500,00 183,15 1,00
68,00 514,58 189,14 0,96
70.00 549,92 203,75 0,86
72,00 587,17 219,27 0,76
74,00 626,37 235,73 0,68
76,00 667,61 253,18 0,60
78,00 710,96 271,66 0,52
80,00 756,50 291 ,22 0,45
82,00 804,28 311 .90 0,38
84,00 854,40 333.74 0,32
86,00 906,93 356,79 0,26
88,00 961,94 381 ,11 0,20
90,00 1019,52 406,74 0,15
92,00 1079,74 433,73 0,10
9400 1142,68 462,13 0,06
96,52 1225,99 500,00 0,00
Gula Aux. José Luis Huanca P.
Teb(ºC)
67.09
896.5
y¡A
1,00
0,98
0,94
0,90
0,85
0,80
0,74
0,68
0.61
0,55
0,47
0,39
0,31
0,22
o,13
0,00
Página 155
UPLOADED BY JORGE BLANCO CHOQUE
UPLOADED BY JORGE BLANCO CHOQUE](https://image.slidesharecdn.com/operacionesunitariaspet-245umsacompleto-220415125942/85/OPERACIONES-UNITARIAS-PET-245-UMSA-COMPLETO-pdf-156-320.jpg)