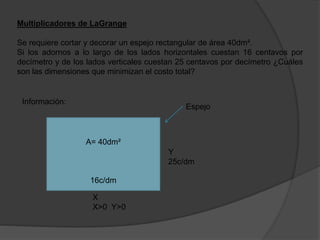
1) El documento describe el método de LaGrange para resolver ecuaciones y sistemas de ecuaciones. 2) Incluye ejemplos de aplicar el método para encontrar valores de X e Y que minimizan el costo total de cortar y decorar un espejo rectangular. 3) Explica cómo usar las condiciones de Kuhn-Tucker para resolver problemas de optimización con restricciones.

1. República Bolivariana de Venezuela
Instituto Universitario Politécnico
“Santiago Mariño” Extensión Porlamar
Manuel Mier y Teran
C.I 19.318.690

2. Método de LaGrange
Y= X² + 3
Tabulación X=3.
X Y Solución
0 3 Y= (0)² +3= 3
1 4 Y= (1) ² +3= 4
4 19 Y= (4) ² + 3= 19
6 39 Y= (6) ² + 3= 39
Introduciendo diferentes valores de X en la ecuación se obtuvo los
valores respectivos en Y.

3. F0(X) = (X-1) (X-4) (X-6)
(0-1) (0-4) (0-6)
F1(X) = (X-0) (X-4) (X-6)
(1-0) (1-4) (1-6)
F2(X) = (X-0) (X-1) (X-6)
(4-0) (4-1) (4-6)
F3(X) = (X-0) (X-1) (X-4)
(6-0) (6-1) (6-4)
=
=
=
=
- 0.25
0.6
0.75
-0.1
Utilizando las formulas y evaluando con los diferentes valores de X,
obtenemos los valores de 0,1,2 y 3 como se muestra en este caso.

4. P(X)= 3² (X-1) (X-4) (X-6)+4² (X-0) (X-4) (X-6)+ 19² (X-0) (X-1) (X-6) + 39² (X-0) (X-1) (X-4)
(0-1) (0-4) (0-6) (1-0) (1-4) (1-6) (4-0) (4-1) (4-6) (6-0) (6-1) (6-4)
P(x) = 12.
Se realiza el polinomio P(X=3) con la formula mostrada, en donde se multiplican los valores de Y
con el valor obtenido de cada función evaluada, obteniendo el resultado final del polinomio.

5. Multiplicadores de LaGrange
Se requiere cortar y decorar un espejo rectangular de área 40dm².
Si los adornos a lo largo de los lados horizontales cuestan 16 centavos por
decímetro y de los lados verticales cuestan 25 centavos por decímetro ¿Cuáles
son las dimensiones que minimizan el costo total?
A= 40dm²
16c/dm
Espejo
Información:
Y
25c/dm
X
X>0 Y>0

6. Función Objetivo:
C=Costo
C= (2X)x16 + (2Y)x25 Costo decoración Vert.
Costo decoración Horz.
C= 32X+50Y
F( x, y) = 32X+50Y
Restricciones:
X.Y= 40 x.y-40=0
G(x,y)= X.Y-40

7. ▼F = ʎ. ▼G
(Fx,Fy)= ʎ(Gx,Gy)
Fx= ʎGx Fy= ʎGy
ʎ= Fx ʎ= Fy
Gx Gy
Fx = Fy
Gx Gy
Derivadas Parciales:
F( x, y) = 32X+50Y G(x,y)= X.Y-40
Fx= 32 Gx=y
Fy= 50 Gy=x
32 = 50
Y X
32X=50Y ÷2 (cada lado de la igualdad)= 16X=25Y

8. 1) 16X=25Y
R) X.Y= 40
Despejamos X en la 1)
X=25Y
16
Seria nuestra función numero 2.
Ahora sustituimos 2 en la función R.
25Y . Y=40
16
25y² =40
16
y² =40x16 Simplificando con quinta quedaría= y² = 8x16= 128=
25 5 5
____
Y= √ 128
5
Y= 5.06 dm

9. Ahora se encontrara X por medio de la función numero 2 sustituyendo a Y.
X= 25x(5.06)
16
X= 7.91 dm.
Seguidamente el punto X y el punto Y forman parte del punto critico de la función
objetivo.
Punto Critico: ( 7.91 ; 5.06)
Comprobación: xy=40
X Y C=32X + 50Y
7.91 5.06 =32(7.91)+50(5.06)= 506.12
10 4 =32(10)+50(4)= 520
20 2 =32(20)+50(2) = 740
Primeramente se calcula los valores obtenidos en X y Y sustituyendo en la
función objetivo, luego ponemos valores arbitrarios que cumplan con la
restricción xy=40. es decir 10x4=40 la cumple, y 20x2=40 la cumple.
Valor min.
Respuesta:
X=7.91dm
Y=5.06 dm

10. Matriz Jacobiana
Ъ =Derivada Parcial.
1) Escriba la Matriz Jacobiana de la función:
Ƒ(x,y) = (x²+3y², 5x³+2y^6) ,donde F1= x²+3y² y F2= 5x³+2y^6.
J Ƒ(x,y) = Ъf1 Ъf1
Ъx Ъy
Ъf2 Ъf2
Ъx Ъy
J Ƒ(x,y) = 2x 6y
15x² 12y^5 2x2

11. Determinante Jacobiano
1) El determinante de jacobiano de la función F: R³ R³ definida como:
Ƒ(x1, x2,x3) = (5x2, 4x² -2sin(x2x3), x2x3)
1
J(x1, x2,x3) = 0 5 0
8x1 -2x3cos(x2x3) -2x2cos(x2x3)
0 x3 x2
= -5x 8x1 -2x2cos(x2x3)
0 x2
= -40x1x2.

12. Condición Kuhn Tucker
Encuentre los valores mínimo y máximo de la función Ƒ(x1, x2)= 3-x1-x2 sujeto a
las restricciones 0 ≤ x1, 0 ≤ x2 y 2x1 + x2 ≤2.
Primero cambiar las restricciones a la forma g ≤0.
0 ≤ x1 g1= - x1 ≤0
0 ≤ x2 g2= - x2 ≤0
X1 + x2 ≤2 g3= 2 x1 + x2 -2 ≤0
Luego se resuelve el problema de minimización primeramente:
m
Ъf(Xo) + ∑ ʎi ЪGi(Xo) = -1+2 ʎ1 -ʎ2 = 0
ЪX1 i=1 ЪX1
m
Ъf(Xo) + ∑ ʎi ЪGi(Xo) = -1 + ʎ1- ʎ3 = 0
ЪX2 i=1 ЪX1

13. Condición de Holgura Complementaria
ʎ1G1 = ʎ1 (2x1 + x2 – 2) = 0
ʎ2G2 = -ʎ2x1 = 0
ʎ3G3 = -ʎ3x2 =0
X1 X2 ʎ1 ʎ2 ʎ3 G1 G2 G3 F
0 0 0 -1 -1 -2 0 0 3
1 0 1/2 0 -1/2 0 -1 0 2
0 2 1 1 0 0 0 -2 1

14. Para determinar el máximo las condiciones quedan de la siguiente manera:
m
- Ъf(Xo) + ∑ ʎi ЪGi(Xo) = -1+2 ʎ1 -ʎ2 = 0
ЪX1 i=1 ЪX1
m
- Ъf(Xo) + ∑ ʎi ЪGi(Xo) = -1 + ʎ1- ʎ3 = 0
ЪX2 i=1 ЪX1
Condición de Holgura complementaria:
ʎ1G1 = ʎ1 (2x1 + x2 – 2) = 0
ʎ2G2 = -ʎ2x1 = 0
ʎ3G3 = -ʎ3x2 =0
X1 X2 ʎ1 ʎ2 ʎ3 G1 G2 G3 F
0 0 0 1 1 -2 0 0 3
1 0 -1/2 0 1/2 0 -1 0 2
0 2 -1 -1 0 0 0 -2 1

15. Observamos que las tablas de minimización y de maximización son idénticas
salvo que los valores de los multiplicadores están cambiados de signo. Por
tanto, la estrategia conveniente para optimizar la función sujeta a restricciones
de desigualdad por el método de las condiciones de Kuhn Tucker será:
1) Plantear el problema como si se tratara solo de minimización y resolver el
sistema de ecuaciones correspondientes.
2) Eliminar aquellos puntos encontrados que no satisfacen las restricciones G1
≤0 .
3) Eliminar aquellos puntos que tienen a la vez multiplicadores positivos y
negativos.
4) Para minimización: escoger dentro de aquellos puntos que tienen
multiplicadores no negativos, aquellos que tienen la menor evaluación de
función objetivo.
5) Para maximización: escoger dentro de aquellos puntos que tienen
multiplicadores no positivos, aquellos que tienen la mayor evaluación de la
función objetivo.