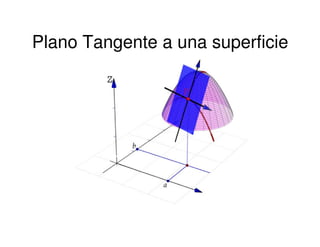
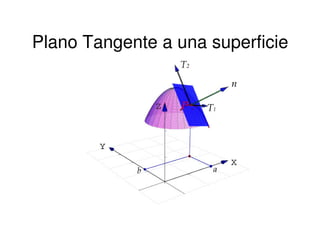
Este documento explica conceptos fundamentales relacionados con los planos tangentes y rectas normales a superficies. Define el plano tangente como aquel que pasa por un punto P de una superficie y contiene a las rectas tangentes a las curvas en dicho punto. Explica cómo calcular la ecuación del plano tangente y de la recta normal mediante el uso de derivadas parciales. También cubre conceptos como puntos críticos y cómo determinar extremos locales de funciones de varias variables.

1. Plano Tangente a una superficie

2. Plano Tangente a una superficie

3. Sea z= f (x , y) una función escalar con
derivadas parciales continuas en (a , b) del
dominio de f . El plano tangente a la superficie
en el punto P( a, b, f(a, b)) es el plano que pasa
por P y contiene a las rectas tangentes a las
Plano Tangente a una superficie
por P y contiene a las rectas tangentes a las
dos curvas



=
=
ax
yxfz
C
),(
:1



=
=
by
yxfz
C
),(
:2

4. Plano Tangente a una superficie

5. Ecuación del Plano tangente
Dirección de un vector tangente a C1 en P
( )),(,0,1 bafu x=
r
Dirección de un vector tangente a C2 en P
( )),(,1,0 bafv y=
r

6. Ecuación del Plano tangente
Dirección de un vector normal del plano
tangente a la superficie en P es:
kji
rrr
rrr
=×=
( )1),,(),,( bafbafn yx −−=
r
),(10
),(01
baf
bafvun
y
x
rrr
=×=

7. Ecuación del Plano tangente
( )),(,, bafbaPPunto por donde pasa el
plano:
Punto genérico del plano: ( )zyxX ,,
( ) 0),()(),()(),( =−−−+− bafzbybafaxbaf yx
Ecuación normal del plano:
( ) 0=−• PXn
rrr

8. Recta normal a una superficie
Sea una función escalar con derivadas parciales
continuas en (a , b) del dominio de f. La recta que
pasa por el punto P( a, b, f (a, b)) en la dirección
del vector
( )1),,(),,( −= bafbafn
r
se conoce como recta normal a la superficie en el
punto P.
( )1),,(),,( −= bafbafn yx
r

9. Ecuación de la recta normal
( )),(,, bafbaPPunto por donde pasa la
recta:
Punto genérico de la recta: ( )zyxX ,,
Ecuación simétrica de la recta normal:
1
),(
),(),( −
−
=
−
=
− bafz
baf
by
baf
ax
yx
Dirección de la recta: ( )1),,(),,( −= bafbafn yx
r

10. Plano Tangente y recta normal a
una superficie
0),,( =zyxF
Sea S una superficie de ecuación dada por:
Sea P (a, b, c) un punto de SSea P (a, b, c) un punto de S
Sea C una curva contenida en S que pasa por
P, definida por la función vectorial
ktzjtyitxtr
rrrr
)()()()( ++=

11. Plano Tangente y recta normal a
una superficie
( ) 0)(),(),( =tztytxF
Entonces F sobre los puntos de la curva vale:
Si F es diferenciable y existen las derivadas
de x, y ,z con respecto a t, de la regla de la
cadena se sigue :
( ) 0=′ tF

12. Plano Tangente y recta normal a
una superficie
x
y
t
t
xF
F
)(tx ′
y tF
yF )(ty ′
z tzF
)(tz ′

13. Plano Tangente y recta normal a
una superficie
( )
0)(),,()(),,()(),,(
0
=′+′+′
=′
tzzyxFtyzyxFtxzyxF
tF
zyx
En el punto (a, b, c), expresado en forma
vectorial sería:
0)(),,( 0 =′•∇ trcbaF
rr
Gradiente Vector tangente a la curva

14. Plano Tangente y recta normal a
una superficie
El gradiente en P es ortogonal al vector
tangente de toda curva contenida en S que
pase por P.
Todas las rectas tangentes en P están en un
plano que es normal al gradiente de F en P y
0)(),,( 0 =′•∇ trcbaF
rr
Gradiente Vector tangente a la curva
plano que es normal al gradiente de F en P y
contiene a P.

15. Plano Tangente y recta normal a
una superficie
Sea F diferenciable en un punto P (a, b, c) de la
superficie S dada por:
0),,( =zyxF con 0),,( ≠∇ cbaF
r
El plano que pasa por P y es normal a ),,( cbaF∇
r
se llama el plano tangente a S en P.
La recta que pasa por P en la dirección de ),,( cbaF∇
r
se llama la recta normal a S en P.

16. Ecuación del plano tangente a una
superficie
Sea F diferenciable en un punto P (a, b, c), una
ecuación del plano tangente a la superficie S
dada por en (a, b, c) es0),,( =zyxFdada por en (a, b, c) es0),,( =zyxF
0))(,,()(),,()(),,( =−+−+− czcbaFbycbaFaxcbaF zyx

17. Ecuación de la recta normal a una
superficie
Sea F diferenciable en un punto P (a, b, c), una
ecuación de la recta normal a la superficie S
dada por en (a, b, c) es0),,( =zyxF
),,(),,(),,( cbaF
cz
cbaF
by
cbaF
ax
zyx
−
=
−
=
−

18. Plano tangente a un paraboloide
22
4 yxz −−=

20. Extremos absolutos y extremos
relativos

21. Extremos absolutos
Sea f (x, y) una función de dos variables
definida y continua en una región cerrada y
acotada D del plano xy
Existe al menos un punto en D donde fExiste al menos un punto en D donde f
alcanza un valor mínimo.
Existe al menos un punto en D donde f
alcanza un valor máximo.
),(),(),( dcfyxfbaf ≤≤
Mínimo absoluto de f en D Máximo absoluto de f en D

22. Mínimo absoluto

23. Extremos relativos
Sea f (x,y) definida y continua en una región
D que contiene el punto (a, b)
La función f tiene un mínimo relativo en (a, b) si
para todo (x,y) en un disco abierto que contiene
a (a, b).
),(),( bafyxf ≥

24. Extremos relativos
Sea f (x,y) definida y continua en una región
D que contiene el punto (a, b)
La función f tiene un máximo relativo en (a, b) si
para todo (x,y) en un disco abierto que contiene
a (a, b).
),(),( bafyxf ≤

25. Puntos críticos
Sea f definida en una región abierta D que
contiene a (a, b). El punto (a, b) es un punto
crítico de f si en él se da alguna de estas
circunstancias:
0),( =bafx y1. 0),( =bafy
2. existenno),(o),( bafbaf yx

26. Los extremos relativos sólo pueden
ocurrir en puntos críticos
Si f está definida en una región abierta D y tiene
en (a, b) un extremo relativo, entonces (a, b) es un
punto crítico de f.
Si f está definida en una región abierta D y tiene
en (a, b) un punto crítico de f, entonces (a, b)
puede ser o no un extremo relativo de f.

27. Función sin máximo ni mínimo
22
),( yxyxf −=

28. Función con máximo sin derivadas

29. El criterio de las segundas
derivadas parciales
Sea f una función con segundas derivadas
parciales continuas en una región abierta que
contiene al punto (a, b) en el cual
0),( =baf y 0),( =bafy0),( =bafx y 0),( =bafy
Para buscar los extremos relativos de f,
utilizamos la cantidad
[ ]2
),(),(),( bafbafbafd xyyyxx −=

30. ).,(enrelativo
mínimountiene,0),(y0Si
ba
fbafd xx >>
).,(enrelativo
máximountiene,0),(y0Si
ba
fbafd xx <>
).,(enrelativo ba
( )
silla.
puntounes),(,,entonces0Si bafbad <
e.concluyent
esnocriterioelentonces0Si =d

31. Valores extremos de
xyyxyxf 42),( 24
−+=

32. Multiplicadores de Lagrange
Deseamos hallar el rectángulo de área
máxima que se pueda inscribir en la elipse
1
43 2
2
2
2
=+
yx3
4
(x,y)
43 22
−4 −3 −2 −1 1 2 3 4 5
−4
−3
−2
−1
1
2

33. Multiplicadores de Lagrange
El rectángulo tiene lados 2x y 2y
2
3
4
(x,y)
Función objetivo
yxyxf 4),( =
−4 −3 −2 −1 1 2 3 4 5
−4
−3
−2
−1
1
2
yxyxf 4),( =
Vínculo o ligadura
1
43 2
2
2
2
=+
yx

34. Multiplicadores de Lagrange
Interpretamos la ecuación de ligadura
1
43 2
2
2
2
=+
yx
43
como una curva de nivel fija de
2
2
2
2
43
),(
yx
yxg +=

35. Multiplicadores de Lagrange
kyxyxf == 4),(
Las curvas de nivel de f
es una familia de hipérbolas.
Las curvas de nivel de f en las que hay
puntos que satisfacen la ligadura o el vínculo
corresponden a las hipérbolas que cortan a la
elipse.

36. Multiplicadores de Lagrange
1
2
3
4
k=20
k=24
k=30
k=36
−4 −3 −2 −1 1 2 3 4 5
−4
−3
−2
−1
1
k=16
k=20
k=12

37. Multiplicadores de Lagrange
3
4 k=30
k=36
1 2 3 4 5
1
2
k=16
k=20
k=24
k=12

38. Multiplicadores de Lagrange
3
4 k=30
k=36
1 2 3 4 5
1
2
k=16
k=20
k=24
k=12

39. Teorema de Lagrange
Sean f y g funciones con primeras derivadas
parciales continuas, tales que f tiene un
extremo en el punto (a, b) sobre la curva
suave de ligadura g (x, y)=c.
0),( ≠∇ bag
r
Si 0),( ≠∇ bag
r
existe un número λ tal que
),(),( bagbaf ∇=∇
rr
λ

40. Método de los multiplicadores de
Lagrange
Sean f y g que satisfacen el teorema de
Lagrange, tales que f tiene un extremo sujeto a
la condición g (x, y)=c. Para hallar el mínimo o
el máximo de f, basta proceder como sigue.
1. Resolver simultáneamente las ecuaciones
),(),( yxgyxf ∇=∇
rr
λ y
cyxg =),(

41. Método de los multiplicadores de
Lagrange
O sea resolver el sistema de ecuaciones en x,
y y λ
),(),( yxgyxf xx λ=
λ=
cyxg =),(
2. Evaluar f en cada uno de los puntos solución
obtenidos en el paso anterior. El mayor de esos
valores da el máximo de f sujeta a la ligadura y
el menor da el mínimo de f sujeta a la ligadura.
),(),( yxgyxf yy λ=

42. Cálculo de los extremos absolutos
Sea z = f (x, y) una función de dos variables
definida y continua en una región cerrada y
acotada D del plano xy entonces f alcanza su
máximo y mínimo absoluto
En los puntos fronteras de D.
En los puntos críticos de f en el interior de D.
Comparando los valores se determinan el
valor máximo absoluto y el mínimo absoluto
de f en D.