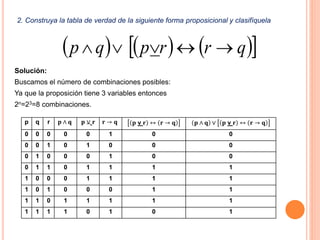
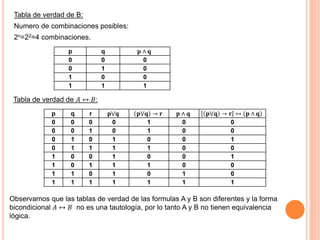
Este documento contiene las soluciones a 5 problemas relacionados con proposiciones lógicas y tablas de verdad. En la primera pregunta, se identifican cuáles enunciados son proposiciones y cuáles no. La segunda pregunta involucra construir la tabla de verdad de una expresión lógica y determinar su clasificación. La tercera pregunta evalúa la equivalencia lógica entre dos fórmulas. La cuarta pregunta halla el dominio de verdad de una función proposicional. Finalmente, la quinta pregunta

1. UNIVERSIDAD FERMIN TORO
CABUDARE ESTADO LARA
I EVALUACIÓN DE ESTRUCTURAS DISCRETAS I
ANGELA ALVARADO
C.I:19114189
AGOSTO 2016

2. 1. A continuación se tienen enunciados que son proposiciones y algunos que no lo son,
explica por qué algunos de estos enunciados son o no proposiciones
a) La tierra es plana.
b) 12 + 28 = 21
c) x > y + 1
d) Hola ¿Qué tal?
e) Bogotá es la capital de Colombia
f) Lava el coche, por favor.
Solución:
a) Si es una proposición ya que su respuesta podría tomar el valor de verdadero o
falso.
b) Si es una proposición ya que el resultado podría tomar el valor de verdadero o
falso.
c) Si es una proposición ya que su resultado que depende de los valores de la
variables x e y podría ser verdadero o falso.
d) No es una proposición ya que su respuesta no puede tomar los valores de
verdadero o falso.
e) Si es una proposición ya que su respuesta puede tomar los valores de verdadero
o falso.
f) No es una proposición ya que su respuesta no puede tomar los valores de
verdadero o falso.

3. 2. Construya la tabla de verdad de la siguiente forma proposicional y clasifíquela
Solución:
Buscamos el número de combinaciones posibles:
Ya que la proposición tiene 3 variables entonces
2n=23=8 combinaciones.
      qrrpqp 
p q r 𝐩 ∧ 𝐪 𝐩 ∨ 𝐫 𝐫 → 𝐪 𝐩 v 𝐫 ↔ 𝐫 → 𝐪 𝐩 ∧ 𝐪 ∨ 𝐩 v 𝐫 ↔ 𝐫 → 𝐪
0 0 0 0 0 1 0 0
0 0 1 0 1 0 0 0
0 1 0 0 0 1 0 0
0 1 1 0 1 1 1 1
1 0 0 0 1 1 1 1
1 0 1 0 0 0 1 1
1 1 0 1 1 1 1 1
1 1 1 1 0 1 0 1

4. Dado que los valores de verdad del operador principal son verdaderos y falsos, y el
operador principal es una disyunción inclusiva entonces la proposición es disyuntiva de
contingencia.
Solución:
Diremos que A y B son lógicamente equivalentes si y solo si la forma bicondicional 𝐴 ↔
𝐵 es una tautología o también podemos probar que el resultado de sus tablas de
verdad son iguales.
Tabla de verdad de A:
Numero de combinaciones posibles:
2n=23=8 combinaciones.
2. Determine si entre las formulas A y B existe equivalencia lógica.
  rqpA :  qpB :
p q r 𝐩⋁𝐪 𝐩⋁𝐪 → 𝐫
0 0 0 0 1
0 0 1 0 1
0 1 0 1 0
0 1 1 1 1
1 0 0 1 0
1 0 1 1 1
1 1 0 1 0
1 1 1 1 1

5. Tabla de verdad de B:
Numero de combinaciones posibles:
2n=22=4 combinaciones.
p q 𝐩 ∧ 𝐪
0 0 0
0 1 0
1 0 0
1 1 1
Tabla de verdad de 𝐴 ↔ 𝐵:
p q r 𝐩⋁𝐪 𝐩⋁𝐪 → 𝐫 𝐩 ∧ 𝐪 𝐩⋁𝐪 → 𝐫 ↔ 𝐩 ∧ 𝐪
0 0 0 0 1 0 0
0 0 1 0 1 0 0
0 1 0 1 0 0 1
0 1 1 1 1 0 0
1 0 0 1 0 0 1
1 0 1 1 1 0 0
1 1 0 1 0 1 0
1 1 1 1 1 1 1
Observamos que las tablas de verdad de las formulas A y B son diferentes y la forma
bicondicional 𝐴 ↔ 𝐵 no es una tautología, por lo tanto A y B no tienen equivalencia
lógica.

6. 4. Hallar el dominio de verdad de la siguiente función proposicional (A.P(X)), donde A=
−2, −1,0,1,2,3,4 y P(x): 2𝑥 + 2 ≥ 4
Solución:
Si x=-2 entonces 2 −2 + 2 ≥ 4 ⟹ −2 ≥ 4 la proposición es falsa.
Si x=-1 entonces 2 −1 + 2 ≥ 4 ⟹ 0 ≥ 4 la proposición es falsa.
Si x=-0 entonces 2 0 + 2 ≥ 4 ⟹ 2 ≥ 4 la proposición es falsa.
Si x=1 entonces 2 1 + 2 ≥ 4 ⟹ 4 ≥ 4 la proposición es verdadera.
Si x=2 entonces 2 2 + 2 ≥ 4 ⟹ 6 ≥ 4 la proposición es verdadera.
Si x=3 entonces 2 3 + 2 ≥ 4 ⟹ 8 ≥ 4 la proposición es verdadera.
Si x=4 entonces 2 4 + 2 ≥ 4 ⟹ 10 ≥ 4 la proposición es verdadera.
Por lo que el dominio de verdad de P(x) es:{1,2,3,4}

7. 5. Encontrar la negación de las siguientes proposiciones:
Solución:
Para a.
Sea 𝑃 𝑥 = 2 + 3 ≤ 10
Entonces ¬𝑃 𝑥 = 2 + 3 > 10
Entonces la negación será:
∀𝑥 ∈ ℜ 2 + 3 > 10
Para b.
Sea 𝑃 𝑥 = 𝑥 + 3 ≥ 7 → 𝑥 + 5 ≤ 8
Entonces ¬𝑃 𝑥 = 𝑥 + 3 ≥ 7 ∧ ¬ 𝑥 + 5 ≤ 8
Entonces la negación será:
∃𝑥 ∈ ℜ 𝑥 + 3 ≥ 7 ∧ ¬ 𝑥 + 5 ≤ 8
  1032)  xxa
  8573)  xxxb