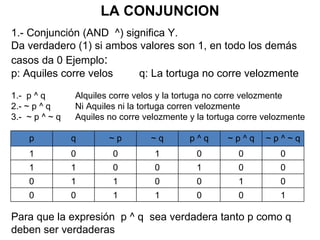
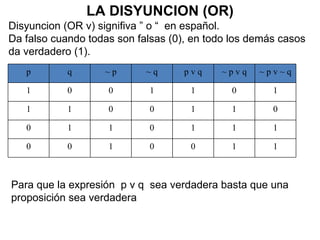
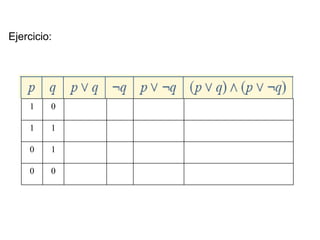
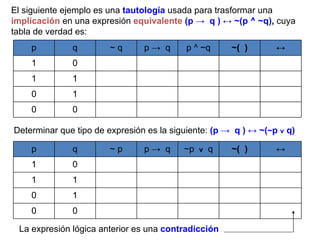
El documento introduce conceptos básicos de lógica proposicional como proposiciones, tablas de verdad, operadores lógicos como conjunción, disyunción, negación e implicación. Explica que la lógica es la ciencia que estudia las formas válidas de razonamiento y las leyes del pensamiento, y que tiene aplicaciones importantes en informática.

1. UNIVERSIDAD PEDAGOGICA NACIONAL ESTRUCTURAS DISCRETAS P R E U F O D

2. L O G I C A

3. INTRODUCCION El ser humano, a través de su vida diaria, se comunica con sus semejantes a través de un lenguaje determinado (oral, escrito, etc.) por medio de las denominadas frases u oraciones. Estas pueden tener diferentes significados pero siempre van a resumirse a las formas de verdaderas o falsas, siendo éste el precedente fundamental para el desarrollo humano. Lo importante en el presente estudio es el hecho de que, a partir de los enunciados y de acuerdo a su significado es posible establecer una proposición y a partir de un conjunto de éstas podemos llegar a una conclusión o inferencia, siendo la lógica la ciencia encargada del estudio de éstas. Hoy en día, la lógica proposicional tiene una importancia singular dada su aplicación en la informática.

4. QUE ES LA LOGICA? Disciplina que estudia los principios formales del conocimiento humano, es decir, las formas y las leyes más generales del pensamiento humano considerado puramente en sı mismo, sin referencia a los objetos.

5. PROPOSICIONES Y ENUNCIADOS LOGICOS Es el significado de cualquier frase declarativa que puede ser verdadero o falso. A las proposiciones o enunciados se les puede asignar uno de dos valores “1” si es verdadero o “0” si es falso , por ese motivo se le denomina logica bivalente

6. Algunos ejemplos de enunciados y propocisiones La frase “1=1” es un enunciado , puesto que puede ser verdadero o falso “ Llovera manana” es una proposicion , para conocer su valo de verdad tenemos que esperar hasta manana. “ Las rosas son rojas y la violetas azules” es un enunciado compuesto por los subenunciados “Las rosas son rojas” y “Las violetas azules” X+2=5 es una ecuacion que adquiere un valor de verdad o falsedad cuando a X se le asignen diferentes valores, por tal razon se denomina una proposicion condicional

7. TABLAS DE VERDAD Es una herramienta desarrollada por Charles Peirce en los años 1880 , siendo sin embargo más popular el formato que Ludwig Wittgenstein desarrolló en su Tractatus logico-philosophicus , publicado en 1918 por Bertrand Russell . Se emplean en lógica para determinar los posibles valores de verdad de una expresión o proposición . O si un esquema de inferencia , como argumento , es formalmente válido mostrando que, efectivamente, es una tautología .

9. LA NEGACION (NOT ~ ) Para negar una proposicion se emplea el simbolo ( ~ ) de tal rorma que ~p ( que se lee “ no p”) Ejemplo: p q 1 1 1 0 0 1 0 0 ~ p 0 0 1 1 ~ q 0 1 0 1

10. LEY DE DOBLE NEGACION (NOT ~ ) Cuando el número de negaciones de un enunciado es par, el valor de verdad de dicho enunciado es el original de la proposición, y cuando es impar es la negación del enunciado original. Ejemplo. ~ ~ p = p ~ ~ ~ p = ~ p ~ ~ ~ ~ p = p ~ ~ ~ ~ ~ p = ~ p

11. PROPOSICIONES COMPUESTAS Una proposición compuesta es una proposicion que se puede descomponer en 2 o mas proposiciones atomicas. Una proposicion atomica es una propocion que no se puede descomponer en mas proposiciones. una proposicion atomica: P = es de noche otra proposicion atomica: Q = esta lloviendo Una PROPOSICION COMPUESTA: P^Q= (P y Q) = Es de noche y esta lloviendo. Las proposiciones compuestas básicas son: La conjunción La disyunción La disyunción exclusiva La implicación La equivalencia

12. 1.- Conjunción (AND ^) significa Y. Da verdadero (1) si ambos valores son 1, en todo los demás casos da 0 Ejemplo : p: Aquiles corre velos q: La tortuga no corre velozmente 1.- p ^ q Alquiles corre velos y la tortuga no corre velozmente 2.- ~ p ^ q Ni Aquiles ni la tortuga corren velozmente 3.- ~ p ^ ~ q Aquiles no corre velozmente y la tortuga corre velozmente LA CONJUNCION Para que la expresión p ^ q sea verdadera tanto p como q deben ser verdaderas p q ~ p ~ q p ^ q ~ p ^ q ~ p ^ ~ q 1 0 0 1 0 0 0 1 1 0 0 1 0 0 0 1 1 0 0 1 0 0 0 1 1 0 0 1

13. Disyuncion (OR v) signifiva ” o “ en español. Da falso cuando todas son falsas (0), en todo los demás casos da verdadero (1). LA DISYUNCION (OR) Para que la expresión p v q sea verdadera basta que una proposición sea verdadera p q ~ p ~ q p v q ~ p v q ~ p v ~ q 1 0 0 1 1 0 1 1 1 0 0 1 1 0 0 1 1 0 1 1 1 0 0 1 0 0 1 1

14. Ejercicio: 1 0 1 1 0 1 0 0

15. Es verdadera solo en el caso en el que las dos proposiciones tengan diferente valor de verdad. LA DISYUNCION EXCLUSIVA (XOR) La palabra “o” tiene dos significados diferentes: En la oración “ El estudiara en la Pedagógica o en la Católica” la presunción es que puede estar en una pero no en ambas. De modo que “o” se utiliza en el sentido llamado disyunción exclusiva p q p q 0 0 0 0 1 1 1 0 1 1 1 0

16. Es falsa si el antecedente es verdadero y el consecuente es falso. La implicación es una conectiva que se notara con una flecha  ejemplo p  q (p implica q). LA IMPLICACION O CONDICIONAL (  ) La implicaciones también reciben el nombre de teoremas, pueden ser de cuatro formas. 1.- Implicación directa. p -> q 2.- Implicación contraria. q -> p 3.- Implicación reciproca. ~ p -> ~ q 4.- Implicación contra reciproca. ~ q -> ~ p Ejemplo: 1.- Sea p: -1=1 q: (-1) ² = (1) ² p es un antecedente falso q es un consecuente verdadero p -> q -1=1 -> (-2) ² = (-2) ² es una implicacion veradera. p q 0 0 0 1 1 0 1 1 p  q 1 1 0 1

17. Ejemplo implicación Las tablas de verdad de la implicaciones directa y contra reciproca, y de la contraria y reciproca son iguales, por tanto estas implicaciones son equivalentes ( ↔ ) es decir. 1.- ( p -> q) ↔ (~ q -> ~ p) 2.- ( q -> p) ↔ (~ p -> ~ q) Cuando una implicación directa es verdadera y lo es además la implicación contraria las proposiciones son equivalentes ( ↔ ) . ( p -> q) ↔ (~ q -> ~ p) ( q -> p) ↔ (~ p -> ~ q) Contraria y Reciproca Directa y Contra reciproca q 0 1 0 1 p 0 0 1 1 ~ p -> ~ q 1 0 1 1 q -> p 1 0 1 1 ~ q -> ~ p 1 1 0 1 p -> q 1 1 0 1 ~ q 1 0 1 0 ~ p 1 1 0 0

18. LA EQUIVALENCIA La equivalencia es una conectiva logica , p ↔ q que se dice: p entonces q , p si y solo q , p es necesario y suficiente para q La equivalencia es verdadera si ambas proposiciones son verdaderas o si ambas son falsas, es decir: Si la tabla de verdad de las proposiciones es siempre verdadera independientemente de la verdad o falsedad de las proposiciones simples, entonces la expresión es tautológica . Si la tabla de verdad es siempre falsa será una contradicción ; si es verdadera y falsa, la proposición es una contingencia . Contingencia q 0 1 0 1 p 0 0 1 1 p ↔ q 1 0 0 1

19. El siguiente ejemplo es una tautología usada para trasformar una implicación en una expresión equivalente (p -> q ) ↔ ~(p ^ ~q) , cuya tabla de verdad es: Determinar que tipo de expresión es la siguiente: (p -> q ) ↔ ~( ~ p v q) La expresión lógica anterior es una contradicción p q ~ q p -> q p ^ ~q ~( ) ↔ 1 0 1 0 1 0 1 1 1 0 1 0 1 1 0 1 0 1 0 1 1 0 0 1 1 0 1 1 p q ~ p p -> q ~ p v q ~( ) ↔ 1 0 0 0 0 1 0 1 1 0 1 1 0 0 0 1 1 1 1 0 0 0 0 1 1 1 0 0

20. Para realizar las tablas de verdad de proposiciones compuestas, de tres simples se deben construir ocho renglones para cada una de las combinaciones de verdad y falsedad Ejemplo: [ p ^ ~ (q v r ) ] -> [ ( p ^ ~ q ) v ( p ^ ~ r ) ] haciendo : s = p ^ ~ q t = p ^ ~ r p q r ~ q ~ r q v r ~( ) [ ^ ] s t [ v ] -> 0 0 0 1 1 0 1 0 0 0 0 1 0 0 1 1 0 1 0 0 0 0 0 1 0 1 0 0 1 1 0 0 0 0 0 1 0 1 1 0 0 1 0 0 0 0 0 1 1 0 0 1 1 0 1 1 1 1 1 1 1 0 1 1 0 1 0 0 1 0 1 1 1 1 0 0 1 1 0 0 0 1 1 1 1 1 1 0 0 1 0 0 0 0 0 1

21. Para realizar las tablas de verdad de proposiciones compuestas, de tres simples se deben construir ocho renglones para cada una de las combinaciones de verdad y falsedad Ejemplo: [ ~ p -> ( ~ q v ~ r ) ] -> [ ~ ( p -> q ) v ~ ( p -> r ) ] haciendo : s = p -> q t = p -> r p q r ~ p ~ q ~r ~q v ~r [ -> ] s t ~ s ~ t [ v ] -> 0 0 0 1 1 1 1 1 1 1 0 0 0 1 0 0 1 1 1 0 1 1 1 1 0 0 0 1 0 1 0 1 0 1 1 1 1 1 0 0 0 1 0 1 1 1 0 0 0 0 1 1 0 0 0 1 1 0 0 0 1 1 1 1 0 0 1 1 1 1 1 0 1 0 1 0 1 1 0 1 1 1 1 0 1 1 0 0 0 1 1 1 1 0 0 0 1 0 1 1 1 0 0 0 0 1 1 1 0 0 0 1

22. LEYES DEL ALGEBRA DE PROPOSICIONES 1.- Idempotencia 2.- Asociativa 3.- Conmutativa 4.- Distributiva 5.- Identidad 6.- Complemento 7.- D´Morgan

23. 1.- LEYES IDEMPOTENCIA a. p v p ↔ p b. p ^ p ↔ p 2.- LEYES ASOCIATIVA de la disyunción a. (p v q) v r ↔ p v (q v r) Disyunción Conjunción p p v p 0 0 1 1 p p ^ p 0 0 1 1 p q r p v q (p v q) v r q v r p v (q v r) 0 0 0 0 0 0 0 0 0 1 0 1 1 1 0 1 0 1 1 1 1 0 1 1 1 1 1 1 1 0 0 1 1 0 1 1 0 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1

24. 2.- LEYES ASOCIATIVA de la conjunción b. (p ^ q) ^ r ↔ p ^ (q ^ r) p q r p ^ q (p ^ q) ^ r q ^ r p ^ (q ^ r) 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 1 1 0 0 1 0 1 0 0 0 0 0 0 1 0 1 0 0 0 0 1 1 0 1 0 0 0 1 1 1 1 1 1 1

25. 3.- LEYES CONMUTATIVAS a. p v q ↔ q v p b. p ^ q ↔ q ^ p Disyunción Conjunción 4.- LEYES DISTRIBUTIVAS a. p v (q ^ r) ↔ (p v q) ^ (p v r) p q p v q q v r 0 0 0 0 0 1 0 0 1 0 0 0 1 1 1 1 p q p ^ q q ^ r 0 0 0 0 0 1 0 0 1 0 0 0 1 1 1 1 p q r q ^ r p v (q ^ r) (p v q) (p v r) (p v q) ^ (p v r) 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 1 0 0 0 1 0 0 0 1 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 0 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1

26. 4.- LEYES DISTRIBUTIVAS b. p ^ (q v r) ↔ (p ^ q) v (p ^ r) 5.- LEYES IDENTIDAD a. p v 0 ↔ p p ^ 1 ↔ p b. p v 0 ↔ p p ^ 1 ↔ p Disyunción Conjunción Disyunción Conjunción p q r q v r p ^ (q v r) (p ^ q) (p ^ r) (p ^ q) v (p ^ r) 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 1 0 1 0 0 0 0 0 1 1 1 0 0 0 0 1 0 0 0 0 0 0 0 1 0 1 1 1 0 1 1 1 1 0 1 1 1 0 1 1 1 1 1 1 1 1 1 p p v 0 0 0 1 1 p p ^ 1 0 0 1 1 p p v 0 0 0 1 1 p p ^ 1 0 0 1 1

27. 6.- LEYES COMPLEMENTO a. p v ~ p ↔ 1 p ^ ~ p ↔ 0 b. ~ ( ~ p) ↔ p -1 = 0, -0 =1 Disyunción Conjunción Ley doble negación 7.- LEYES D´ MORGAN a. ~ (p v q) ↔ ~ p ^ ~ q p p v ~ p 0 1 1 1 p p ^ ~ p 0 0 1 0 p ~ p ~(~ p) 0 1 0 1 0 1 p q p v q ~(p v q) ~ p ~ q ~ p ^ ~ q 0 0 0 1 1 1 1 0 1 1 0 1 0 0 1 0 1 0 0 1 0 1 1 1 0 0 1 0

28. 7.- LEYES D´ MORGAN b. ~ (p ^ q) ↔ ~ p v ~ q p q p ^ q ~(p ^ q) ~ p ~ q ~ p v ~ q 0 0 0 1 1 1 1 0 1 0 1 1 0 1 1 0 0 1 0 1 1 1 1 1 0 0 0 0

29. Argumentos y Reglas de inferencia * ¿Qué es una implicación lógica? * ¿Qué es un argumento? * ¿Qué es un argumento válido? * ¿Cómo usar las reglas de inferencia para establecer y demostrar la validez de un argumento?

30. Recuerda… Equivalencia significa igualdad Las leyes lógicas nos muestran algunas proposiciones equivalentes a otras. Eso equivale a conocer “atajos proposicionales”. ¿Puedes dar un ejemplo de dos proposiciones compuestas que sean lógicamente equivalentes? … . Pasemos a un concepto nuevo

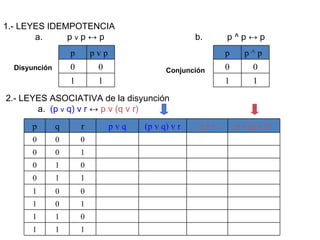
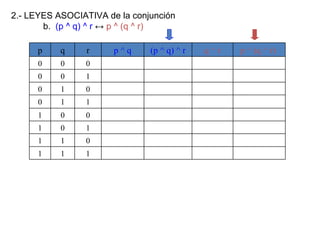
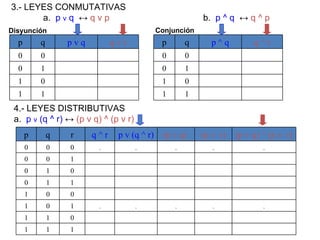
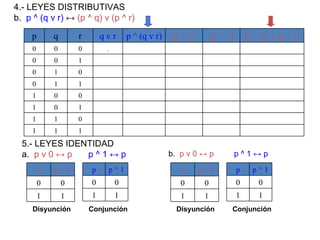
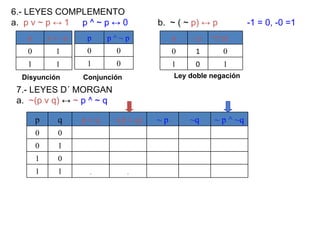
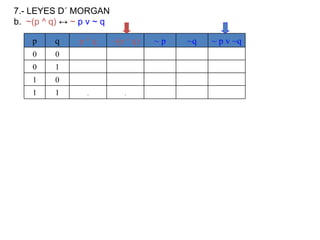
31. ¿Qué es una implicación lógica? Sean r y s dos proposiciones compuestas. Decimos que r implica lógicamente a s cuando r  s es una tautología y lo denotamos por r  s. Esto significa que s es verdadera siempre que r sea verdadera. Ejemplo: Comprueba que [(p  q)  p]  q . En este caso, r es [(p  q)  p] y s es q Piénsalo unos minutos ...!

32. ¿Qué es una implicación lógica? Para comprobar [(p  q)  p]  q usamos la definición. Esta es una implicación lógica llamada: Modus Ponens o Modo Positivo . Está relacionada con un modo de razonamiento: “Si tengo dinero, voy al cine. Y tengo dinero. Por lo tanto, … voy al cine!” p q p  q [ ( p  q)  p] [(p  q)  p]  q. V V V V V V F F F V F V V F V F F V F V

33. ... implicación lógica Observa que: Una implicación lógica NO es lo mismo que una equivalencia lógica. En una equivalencia lógica podemos sustituir una proposición por otra. En la implicación lógica no podemos sustituir una proposición por otra. ¿Puedes dar una razón? Que r  s sea una tautología equivale a decir que s es cierta cada vez que r sea cierta.

34. ... implicación lógica Ejercicio 1: Decide si es o no es cierto que : a)   q  (p  q)   p   q  (p  q)    p [ (p  q)   p ]  q Toma unos minutos para decidir ... a) No es cierto; es falsa si p y q son falsas. b) Es cierto ; a esta implicación se le llama Modus Tollens. c) Es cierto ; a esta implicación se le llama Silogismo disyuntivo.

35. ¿Qué es un argumento? Un argumento es una proposición compuesta del tipo Si (p 1  p 2  p 3  .....  p k ) entonces q Premisas  Conclusión Ejemplo Si Juan se gana la beca, viaja a Par í s. Y Juan se gan ó la beca. Por lo tanto, viajar á a Par í s. Este argumento tiene dos premisas. Las premisas son : “Si Juan gana la beca entonces viaja a París” y “ Juan se ganó la beca”. La conclusión es : “Juan viaja a París”.

36. “ Si Juan se gana la beca, viaja a Par í s. Y Juan se gan ó la beca. Por lo tanto, viajar á a Par í s ” . Este argumento puede representarse como una tabla o como una implicaci ó n. Sean las proposiciones: p: “ Juan gana la beca ” q: “ Juan viaja a Par í s ” . ¿Qué es un argumento? Implicación: [(p  q)  p]  q Tabla: p  q p  q

37. Ejercicio “ Fue Elisa o fue Carlos quien cometió el fraude. Pero Elisa estaba fuera de la ciudad cuando el crimen fue cometido. Si ella estuvo fuera de la ciudad, no pudo cometer el crimen. Eso nos conduce, lógicamente, a Carlos. Él es el culpable.” a) ¿Cuáles son las premisas en este argumento? b) ¿Cuál es la conclusión ? … Argumento Proposiciones simples p : “Elisa cometió el fraude”. q : “Carlos cometió el fraude”. r : “Elisa estaba fuera de la ciudad cuando el crimen fue cometido”. Hay varias premisas y la conclusión es una proposición simple. Premisa 1: p  q Premisa 2: r Premisa 3: r   p Conclusión: q

38. Ejemplo: Expresa simbólicamente “ Si el hijo de Leonidas está vivo, éste se casará con Ivette. Pero el hijo de Leonidas murió, por lo tanto, él no podrá casarse con Ivette.” … Argumento Implicación: {(p  q)   p}   q ¿ Es ésta una implicación lógica? Proposiciones simples: p: “El hijo de Leonidas está vivo” q: “El hijo de Leonidas se casa con Ivette” Tabla: p  q  p   q

39. Se dice que: Un argumento es válido si cada vez que las premisas son verdaderas, la conclusión es verdadera. Es decir, si las premisas son ciertas, está garantizada la veracidad de la conclusión. De modo que un argumento es válido si la implicación: (Premisas)  (Conclusión) es una implicación lógica. Un argumento es válido debido a su forma, no a su contenido. Argumento válido

40. Argumento válido [(p  q)  p]  q Este ES un argumento válido [(p  q)   p]   q Este NO ES un argumento válido. Para comprobar la segunda afirmación, supón que las premisas son verdaderas… y verifica que no puedes asegurar que la conclusión es verdadera

41. Un argumento puede ser válido (debido a su forma) aunque el contenido de la conclusión pueda ser falso. Ejemplo Si Ud. invierte en la Bolsa, se hará rico. Si Ud. se hace rico, será feliz ___________________________ Si Ud. invierte en la Bolsa, será feliz. Comprueba que este es un argumento válido. Argumento válido

42. Son reglas que permiten establecer la veracidad de un argumento sin tener que realizar una gran tabla de verdad. Las reglas están asociadas a formas de razonamiento. Las reglas de inferencia tienen asociadas implicaciones lógicas. Algunas de las más usadas son: el Modus Ponens y el Modus Tollens que ya vimos. Otras son: Silogismo, Silogismo disyuntivo, Simplificación, Amplificación, Demostración por casos. Reglas de Inferencia

43. Reglas de Inferencia Con estas reglas podemos ir de un lado a otro, pero no podemos regresarnos una vez que usamos la garrocha. Silogismo hipotético [(p  q)  (q  r)]  (p  r) Silogismo disyuntivo [( p  q)   p)]  q Nombre de la Regla Implicación lógica Simplificación ( p  q )  p Amplificación p  ( p  q ) Modus Ponens [ p  ( p  q)]  q Modus Tollens [( p  q)   q ]   p

44. Ejemplo: Dado el argumento  (  p   q)  (r  s)]  (r  t)  (  t )   q a) Decida si es o no válido. b) En caso de ser válido, demuéstrelo. Si no es válido, dé un contraejemplo. a) Análisis sobre la validez : Debemos suponer que todas las premisas son ciertas y trataremos de comprobar que la conclusión también lo es. Es conveniente empezar de la premisa más sencilla. Validez de argumentos

45. Hay tres premisas: (  p   q)  (r  s)  (r  t)  (  t ) P1 P2 P3 Comencemos por P3: t es falsa. Por P2: r debe ser falsa. Al ver P1: si r es falsa, r  s es falsa, de modo que el antecedente  p   q es falso. Pero (  p   q)   ( p  q), por lo tanto, ( p  q) es verdadera. Esto ocurre, cuando tanto p como q son verdaderas. De modo que q es verdadera. Validez de argumentos Por lo tanto, el argumento es válido !!!

46. Demostración de la validez b) Demostremos que es válido . Los pasos de la demostración están sugeridos por la parte anterior. Partimos del antecedente y utilizando las leyes lógicas y las reglas de inferencia tratamos de tender los puentes para llegar a la conclusión. … En cada línea justificaremos el paso dado, mencionando el nombre de la ley o de la regla de inferencia que usamos …

47. - Ley usada - [(  p   q)  (r  s)]  (r  t)  (  t )  [(  p   q)  (r  s)]  [(r  t)  (  t )] Asociativa  [(  p   q)  (r  s)]   r Modus Tollens  [(  p   q)  (r  s)]  (  r   s) Amplificación  [(  p   q)  (r  s)]   ( r  s) De Morgan   (  p   q) Modus Tollens   p   q De Morgan  p  q Doble negación  q Reducción Demostración de la validez

48. Ejemplo 2: Dado el argumento  (p  q)  (  r  s)  ( p  s)   (  q  s) a) Decida si es o no válido. b) En caso de ser válido, demuéstrelo. Si no es válido, dé un contraejemplo. a) Sobre la validez : Supongamos que todas las premisas son ciertas y trataremos de demostrar que la conclusión lo es. P1: (p  q) es cierta. P2: (  r  s) es cierta. P3: ( p  s) es cierta. C:  q  s ¿será cierta? … Validez de argumentos

49. P1: (p  q) es cierta. P2: (  r  s) es cierta. P3: ( p  s) es cierta. C:  q  s Por P3: p y s no pueden ser ambas falsas. Caso 1: Supongamos que s es cierta, pero no lo es p . Por P1 : q puede ser verdadera o falsa. En cuyo caso, la conclusión es cierta. Caso 2: Supongamos que p es cierta, pero no lo es s . Por P1: q es cierta. En cuyo caso, (  q  s ) es cierta. Caso 3: Supongamos que p y s son ambas ciertas. Entonces q es cierta. En cuyo caso, (  q  s ) es cierta. Por lo tanto, el argumento es válido ! Decidir sobre la validez

50. b) Sobre la demostración : Partiendo de las premisas, debemos arribar a la conclusión. Completa las reglas o leyes que faltan . - Ley o Regla usada - (p  q)  (  r  s)  ( p  s)   (  p  q)  (  r  s)  ( p  s) sustitución 1    (  p  q)  (p  s)   (  r  s) conm. y asoc.     (  p  q)  p    (  p  q)  s    (  r  s) distribut.   q  [ (  p  q)  s   (  r  s) silog. disyuntivo   q  (  p  s)  (q  s)   (  r  s) ________   q  (  p  s)   (  r  s) ________   (q   p)  (q  s ) ]  (  r  s) _________  (q   p)  (q  s ) _________  (q  s ) __________   q  s __________ Demostrar la validez

51. Se tiene el siguiente argumento, parecido al ejemplo 1  (  p   q)  (r  s)]  (r  t)  (  t)    q P1 P2 P3 Decidamos si es, ó no, válido . Comencemos por P3: t es falsa. Por P2: r debe ser falsa. Al ver P1: como r es falsa, r  s es falsa; de modo que  p   q es falsa, lo cual ocurre cuando  p y  q son falsas … ¿ Y si no es válido?

52. En el argumento: [  (  p   q)  (r  s)]  (r  t)  (  t)]   q P1 P2 P3 La conclusión puede ser falsa aún cuando las premisas son verdaderas !!! … Esto indica que el argumento NO es válido . De hecho, si p, r, s y q son V, F, V y V respectivamente, las premisas son ciertas y la conclusión es falsa. Este es el contraejemplo . ¿Cómo comprobar que no es válido?

53. Ejercicio Decida si el argumento es válido y si lo es, proporcione una demostración. Denote a las proposiciones por p, q, r, s, .. “ Si hay cierta probabilidad de lluvia o pierde su lazo rojo, Lucy no cortará la grama. Siempre que la temperatura supere los 80° F, no hay probabilidad de lluvia. Hoy la temperatura es de 85° F y Lucy está usando su lazo rojo. Por lo tanto, Lucy cortará la grama.”