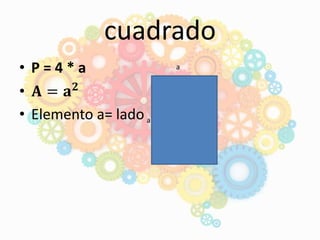
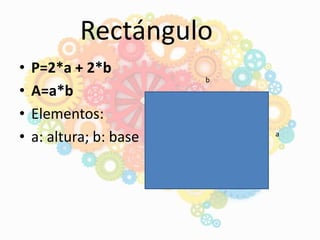
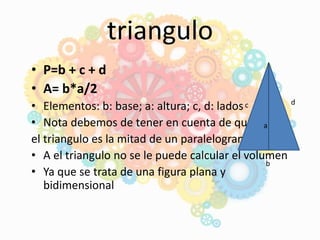
El documento describe los antecedentes necesarios para que los niños aborden el tema del área, perímetro y volumen en preescolar. Explica que los niños deben tener disposición para aprender, manejar números, razonamiento numérico y nociones espaciales. También presenta fórmulas para calcular el área y perímetro de cuadrados, rectángulos y triángulos, y define conceptos como área, perímetro y volumen. Por último, indica que los niños llegan al preescolar con conocimientos previos de números,

2. ¿QUE COSAS TIENEN
QUE SABER EL NIÑO
PARA ABORDAR EL
TEMA?

3. PRIMERO
• Presentar una
disposición para
llevar a cabo el
aprendizaje que se
le plantea .
• Surge de factores
de índole personal
e interpersonal

4. • Disponibilidad de
determinadas
capacidades
instrumentos,
estrategias y
habilidades
generales para
llevar a cabo el
proceso.
• SEGUNDO

5. ¿ como debe
de saber?
• Debe de manejar números.
• La abstracción numérica .
• el razonamiento
numérico.
• desarrollo de las nociones
espaciales

6. ¿ como calcular el área?
• el procedimiento varía con cada
figura, puesto que figuras diferentes
necesitan fórmulas diferentes
• En otras palabras, la fórmula dice
que "el área es igual al producto de
la base por la altura".

7. Pasos
• Mide las dimensiones que se
necesitan en la fórmula que estás
utilizando la que estás trabajando.
• Utiliza una regla o una cinta métrica
para hallar estas medidas
• Incluye estas medidas en la fórmula .

8. En resumen
• el procedimiento dependiendo de la
fórmula que utilices.
• El procedimiento básico es siempre el
mismo
.
• Debes identificar la figura de la que quieres
hallar el área, encontrar la fórmula para
esta, medir las dimensiones que se piden
en la fórmula e inserta dichas medidas en
la fórmula.
• La variación tiene lugar en las medidas que
requieren las diferentes fórmulas.

9. PERIMETRO
• Conjunto de líneas que forman una
superficie o una figura
• La suma de todos los lados de la
figura geométrica.

10. ÁREA
•es la medida de la superficie de
una figura, la medida de su
región interior.

11. VOLUMEN
•es el grosor o el tamaño que posee un objeto.
•sirve para identificar la magnitud física que
informa sobre la extensión de un cuerpo
•posee tres dimensiones, alto, largo y ancho
•Es representado por el metro cubico SIU.

12. Área, perímetro y volumen
Formula para sacar el área, perímetro y
rectángulo del triangulo, cuadrado y rectángulo.

13. • El volumen solo se calcula en
los prismas no en las figuras
planas o bidimensionales
ósea que solo tienes las
medidas de sus lados

14. cuadrado
• P = 4 * a
• 𝐀 = 𝐚 𝟐
• Elemento a= lado
a
a

15. Rectángulo
• P=2*a + 2*b
• A=a*b
• Elementos:
• a: altura; b: base a
b

16. triangulo
• P=b + c + d
• A= b*a/2
• Elementos: b: base; a: altura; c, d: lados
• Nota debemos de tener en cuenta de que
el triangulo es la mitad de un paralelogramo
• A el triangulo no se le puede calcular el volumen
• Ya que se trata de una figura plana y
bidimensional
a
b
c d

17. ejercicios

18. Largo
• es un adjetivo que refiere a aquello que tiene
mucha longitud. Puede utilizarse en sentido físico o
simbólico, dependiendo el contexto.
Todas las cosas tienen una determinada longitud. Esta
noción suele entenderse en conjunto con la idea
de anchura: los objetos, por lo tanto, tienen un largo
y un ancho. Se dice que algo es largo cuando la
longitud supera a la anchura.
En su acepción simbólica, lo largo es aquello extenso,
continuado, dilatado o abundante.

19. Ancho
• Con ancho se denomina a la
dimensión menor de las figuras
planas; la dimensión mayor
correspondiente es el largo. Es
sinónimo de anchura “la menor de
las dos dimensiones principales que
tienen las cosas o figuras planas, en
contraposición a la mayor longitud”.

20. Ancho y largo
Ejercicio de matemáticas para niños de 3
años. Aprender longitudes
Se le pide a niño que identifique y lo señale, cual lado
es el largo y el ancho.

21. • Pedir que identifique y señale cual es más
largo y si su ancho es diferente
Ancho y largo
Ejercicio de matemáticas para niños de 4
años. Aprender longitudes

22. • Se le pedirá que dibujen cuatro figuras en las
cuales, dos tengan el mismo ancho, pero no el
mismo largo, y dos donde tengan el mismo
largo pero no ancho.
Ancho y largo
Ejercicio de matemáticas para niños de 5
años. Aprender longitudes

23. Cuáles son los antecedentes que
consideran necesarios para la
enseñanza del tema en preescolar.
• Los niños llegan con el conocimiento previo de los
números, las formas y la medición. Ya que en sus
primeros años, en su vida cotidiana se mencionan
estos temas de manera informa y al momento de llegar
al preescolar se logra mediante el aprendizaje
sistemático que les proporcionan las educadoras.
• Un niño antes de llegar al jardín ya sabe hablar y en
algunas de sus palabras logra decir por ejemplo “quiero
un color” y es cuando se dice que tiene un previó
conocimiento de lo que es el número.