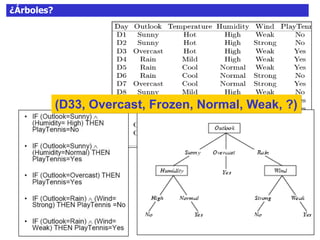
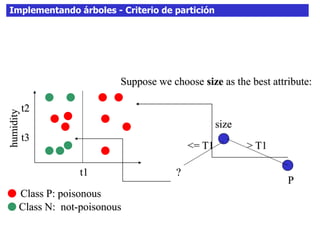
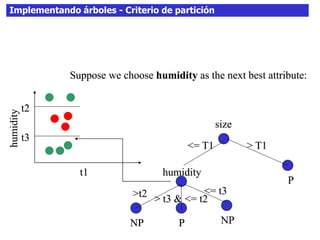
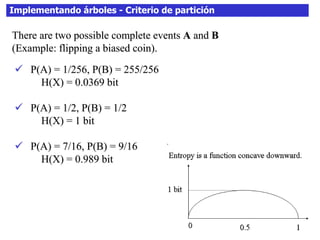
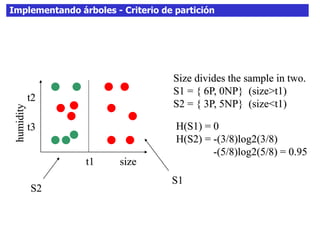
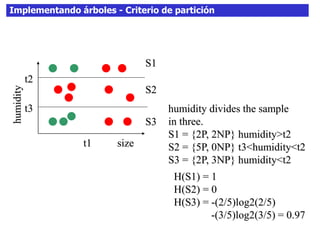
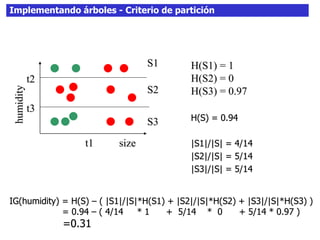
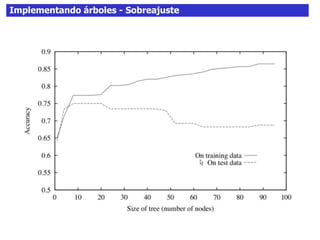
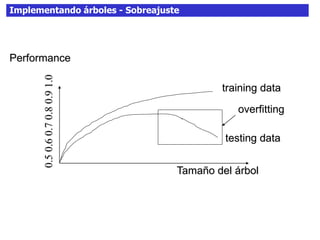
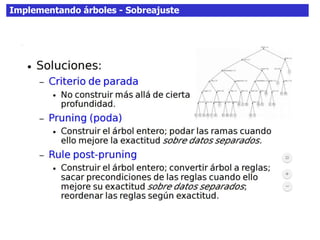
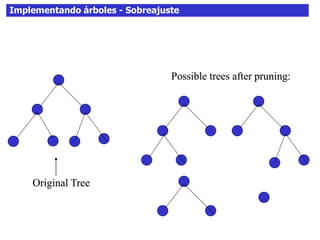
Este documento discute los árboles de decisión, incluyendo cómo inducir árboles a partir de conjuntos de datos clasificados, implementar árboles mediante criterios de partición y parada, y abordar problemas como el sobreajuste. Explica conceptos como la ganancia de información para seleccionar atributos y dividir los datos, así como diferentes enfoques para determinar la profundidad óptima de un árbol.

1. Buenos Aires, marzo de 2016
Eduardo Poggi

2. Analytics – Árboles de decisión
 ¿Induciendo árboles?
 Implementando árboles
 Criterio de selección
 Criterio de parada
 Sobreajuste
 Valores numéricos
 Valores faltantes
 “Árboles se buscan”
 ¿Árboles o bosques?

3. Analytics – Árboles de decisión
 ¿Induciendo árboles?
 Implementando árboles
 Criterio de selección
 Criterio de parada
 Sobreajuste
 Valores numéricos
 Valores faltantes
 “Árboles se buscan”
 ¿Árboles o bosques?

4. ¿Árboles?
 Probablemente el método más conocido para resolver
problemas de clasificación
 Muy asociado a nuestra forma de proceder
 Uno de los primeros desarrollos en ML

5. ¿Árboles?

6. ¿Árboles?
ID3 and its successors have been developed by
Ross Quinlan, who discovered it while
working with Earl Hunt in the 1970s. He
subsequently worked at Sydney Uni, Rand
Corporation in California, UTS, back to Sydney
Uni, and several years at UNSW. He now runs
his own company Rulequest
www.rulequest.com

7. IDT - Induciendo árboles
 IDT : Induction of Decision Trees
 A partir de un conjunto de instancias clasificadas (ejemplos,
evidencia) inducir un árbol de decisión que pueda ser utilizado
para predecir la clase de instancias no clasificadas (y no vistas
previamente).

8. ¿Árboles?
Ejemplos = instancias
clasificadas
Evidencia

9. ¿Árboles?
(D33, Overcast, Frozen, Normal, Weak, ?)

10. ¿Árboles?
 Método de aproximación de funciones de valores
discretos.
 Lenguaje de representación de instancias:
 conjunciones de valores discretos.
 Lenguaje de representación de hipótesis:
 Disyunción de reglas conjuntivas.
 Características:
 Capaz de aprender conceptos disyuntivos.
 Tolerante al ruido en atributos y clase.
 Tolerante a valores faltantes en atributos.
 No incremental.

11. ¿Árboles?
 Estructura de datos recursiva definida por:
 Nodos hoja que indican un rótulo de clase.
 Nodos internos que contienen un test sobre el valor de un
atributo. Para cada resultado del test hay una rama y un subárbol
con la misma estructura que el árbol.
 Representación alternativa:
 conjunto de reglas: IF Condición THEN Clasificación

12. Induciendo árboles
 El problema de encontrar un árbol de decisión que
concuerde con el conjunto de entrenamiento tiene una
solución trivial.
 Simplemente construimos un árbol de decisión que tenga una
rama por cada ejemplo.
 El problema con este árbol trivial es que solo memoriza las
observaciones.
 No extrae ningún patrón a partir de los ejemplos y no puede
extrapolar a ejemplos que no vio.

13. Induciendo árboles
 Extraer un patrón significa poder describir un gran
número de casos de un modo conciso. El lugar de sólo
tratar de encontrar uno que concuerde con los ejemplos,
deberíamos también tratar de encontrar uno conciso.
 Este es un ejemplo de un principio general del
aprendizaje inductivo:
 La hipótesis más probable es la más simple que sea consistente
con todas las observaciones.
¿Hipótesis consistente con
todas las observaciones?

14. Induciendo árboles
 Navaja de Occam (Occam's Razor)
 El principio de economía o de
parsimonia hace referencia a un tipo
de razonamiento basado en una
premisa muy simple:
 En igualdad de condiciones la solución
más sencilla es probablemente la
correcta.
 No ha de presumirse de la existencia de
más cosas que las absolutamente
necesarias.
 No hay que desarrollar sistemas más
complejos que lo necesario.
William of Ockham
(c. 1280/1288– 349)
Fraile franciscano, filósofo y lógico
inglés oriundo de Ockham
¿Es posible construir
sistemáticamente el árbol
“óptimo” en términos de
Occam?

15. Induciendo árboles
 Desafortunadamente, encontrar el árbol de decisión
óptimo (más chico) es un problema intratable, pero
algunas heurísticas simples logran encontrar uno
suficientemente pequeño.
 La idea básica del algoritmo es usar primero el atributo
“más importante”, donde esto significa el que tiene un
efecto más importante en la agrupación de los ejemplos
en conjuntos que comparten la misma clasificación.

16. Induciendo árboles
 ¿Heurística?
 Como metodología científica, la heurística es aplicable a cualquier
ciencia e incluye la utilización de: medios auxiliares, principios,
reglas, estrategias o algoritmos que faciliten la búsqueda de vías
de solución a problemas.
 “Sobre un punto de vista heurístico concerniente a la producción
y transformación de la luz”, Albert Einstein, 1905

17. Analytics – Árboles de decisión
 ¿Induciendo árboles?
 Implementando árboles
 Criterio de selección
 Criterio de parada
 Sobreajuste
 Valores numéricos
 Valores faltantes
 “Árboles se buscan”
 ¿Árboles o bosques?

18. Induciendo árboles
 ID3 (Ejemplos, Clase, Atributos)
 Crear nodo Raíz del árbol
 Todos los Ejemplos tienen la misma Clase?
 retornar rótulo = Clase
 Atributos = ∅ ?
 SI: retornar rótulo = Clase más frecuente
 NO:
 A <- ELEGIR_ATRIBUTO (Atributos, Ejemplos)
 Raíz <- A
 Para cada valor posible v de A
 Agregar una nueva rama debajo de Raíz con test A = v?
 Ejemplos_v <-{elementos de Ejemplos con A = v}
 Ejemplos_v = ∅ ?
 SI: agregar debajo de esta rama un nodo hoja con valor más frecuente de
Clase en Ejemplos
 NO: agregar debajo de esta rama el subárbol ID3 (Ejemplos_v, Clase,
Atributos – {A})
Es un algoritmo?
Clase más frecuente?

19. Implementando árboles - Criterio de partición
 Asumamos que el Criterio de Partición se limita a
seleccionar un atributo.
 ¿Cómo elegir el atributo más “importante” para dividir?
 Muchas aproximaciones:
 Information Gain
 Information ratio
 Gini
 … tantas como autores

20. Implementando árboles
 Existen varios aspectos prácticos a resolver a la hora de
implementar árboles de decisión.
 Cuál es el objetivo del árbol?
 Cuál es un buen criterio de partición?
 Qué tan profundo debe ser el árbol?
 Cómo se pueden incluir atributos continuos?
 Qué pasa cuando hay valores faltantes?
 Cómo podemos afrontar la eficiencia computacional para grandes
evidencias?

21. Implementando árboles - Criterio de partición
Attributes: size and humidity
Size has two values: >t1 or <= t1
Humidity has three values: >t2, (>t3 and <=t2), <= t3
size
humidity
t1
t2
t3
Class P: poisonous
Class N: not-poisonous

22. Implementando árboles - Criterio de particiónhumidity
t1
t2
t3
Suppose we choose size as the best attribute:
size
P
> T1<= T1
Class P: poisonous
Class N: not-poisonous
?

23. Implementando árboles - Criterio de particiónhumidity
t1
t2
t3
Suppose we choose humidity as the next best attribute:
size
P
> T1<= T1
humidity
P NPNP
>t2 <= t3
> t3 & <= t2

24. Implementando árboles - Criterio de partición
 Para decidir cual es el mejor atributo para abrir el árbol:
 Usamos algunas definiciones de Teoría de la Información.
 La medida de incertidumbre o entropía asociada a una variable
aleatorea X se define como:
 H(X) = - Σ pi log2 pi
 Siendo log2 un redefinición de logaritmo en base 2 con log(0)=0.

25. Implementando árboles - Criterio de partición
 P(A) = 1/256, P(B) = 255/256
H(X) = 0.0369 bit
 P(A) = 1/2, P(B) = 1/2
H(X) = 1 bit
 P(A) = 7/16, P(B) = 9/16
H(X) = 0.989 bit
There are two possible complete events A and B
(Example: flipping a biased coin).

26. Implementando árboles - Criterio de partición
Size divides the sample in two.
S1 = { 6P, 0NP} (size>t1)
S2 = { 3P, 5NP} (size<t1)
sizet1
t2
t3
humidity
S1
S2
H(S1) = 0
H(S2) = -(3/8)log2(3/8)
-(5/8)log2(5/8) = 0.95

27. Implementando árboles - Criterio de partición
humidity divides the sample
in three.
S1 = {2P, 2NP} humidity>t2
S2 = {5P, 0NP} t3<humidity<t2
S3 = {2P, 3NP} humidity<t2
H(S1) = 1
H(S2) = 0
H(S3) = -(2/5)log2(2/5)
-(3/5)log2(3/5) = 0.97
sizet1
t2
t3
humidity
S1
S3
S2

28. Implementando árboles - Criterio de partición
sizet1
t2
t3
humidity
Information gain IG over attribute A: IG (A)
IG(A) = H(S) - Σv (Sv/S) H (Sv)
IG(humidity)=0.94 - 4/14*1 - 5/14*0 - 5/14*0.97=0.31

29. Implementando árboles - Criterio de partición
 Definimos la función de Ganancia de Información como:
 IG(A) = H(S) - Σv (Sv/S) H (Sv)
 Donde:
 H(S) es la entropía del conjunto de todos los ejemplos
 H(Sv) es la entropía del subconjunto de los ejemplos con valor v
para el atributo A
 Elegiremos al atributo que maximice la IG, por lo tanto
debemos calcular IG para todos los atributos:

30. Implementando árboles - Criterio de partición
sizet1
t2
t3
humidity
S1S2
H(S1) = 0
H(S2) = 0.95
H(S) = -(9/14)log2(9/14)
-(6/14)log2(6/14) = 0.94
|S1|/|S| = 6/14
|S2|/|S| = 8/14
IG(size) = H(S) – ( |S1|/|S|*H(S1) + |S2|/|S|*H(S2) )
= 0.94 – ( 6/14 * 0 + 8/14 * 0.95) = 0.40

31. Implementando árboles - Criterio de partición
sizet1
t2
t3
humidity
S1
S3
H(S1) = 1
H(S2) = 0
H(S3) = 0.97
H(S) = 0.94
|S1|/|S| = 4/14
|S2|/|S| = 5/14
|S3|/|S| = 5/14
S2
IG(humidity) = H(S) – ( |S1|/|S|*H(S1) + |S2|/|S|*H(S2) + |S3|/|S|*H(S3) )
= 0.94 – ( 4/14 * 1 + 5/14 * 0 + 5/14 * 0.97 )
=0.31

32. Implementando árboles - Criterio de parada
 Hasta cuando dividimos?
 Hasta que tenga clases puras en todos los nodos
 Hasta que no tenga más variables disponibles
 O hay algo mejor?

33. Implementando árboles - Criterio de parada
 La versión canónica dice que el árbol se sigue
desarrollando hasta que se llega a una clase uniforme.
Esto en la práctica no suele ser efectivo.
 Existen muchas opciones de criterio de parada:
 No hay más atributos.
 Clase uniforme.
 Clase mayoritaria.
 Se supera un nivel de profundidad máximo.
 El número de casos es menor a un mínimo.
 El mejor valor del criterio de partición es menor de un umbral.
 El número de casos de los nodos hijos es menor que un mínimo.

34. Implementando árboles - Sobreajuste
La línea verde como clasificador se
adapta mejor a los datos con los
que que se ha entrenado al
clasificador, pero está demasiado
adaptada a ellos, de forma que
ante nuevos datos probablemente
arrojará más errores que la
clasificación usando la línea negra.

35. Implementando árboles - Sobreajuste

36. Implementando árboles - Sobreajuste

37. Implementando árboles - Sobreajuste
0.50.60.70.80.91.0
Tamaño del árbol
training data
testing data
overfitting
Performance

38. Implementando árboles - Sobreajuste
A tree overfits the data if we let it grow deep enough so that it
begins to capture “aberrations” in the data that harm the predictive
power on unseen examples:
size
t2
t3
humidity
Possibly just noise, but
the tree is grown deeper
to capture these examples

39. Implementando árboles - Sobreajuste

40. Implementando árboles - Sobreajuste
 Parar la construcción de la rama antes de sobreajustar
los datos.
 En la práctica no es tan fácil de implementar ya que no es claro
cual es buen punto de parada.
 Dejar crecer el árbol y sobreajustar. Luego ir probando
podas y verificando la performance.
 Este método es que tiene más popularidad en la comunidad.
¿Qué pasa si primero pasamos a reglas y luego podamos?

41. Implementando árboles - Sobreajuste
1.) Grow the tree to learn the
training data
2.) Prune tree to avoid overfitting
the data

42. Implementando árboles - Sobreajuste
Original Tree
Possible trees after pruning:

43. Implementando árboles - Sobreajuste
Pruned Tree
Possible trees after 2nd pruning:

44. Implementando árboles - Sobreajuste
Process continues until no improvement is observed
on the validation set:
0.50.60.70.80.91.0
Size of the tree
validation data
Stop pruning the tree

45. Implementando árboles - Sobreajuste

46. Implementando árboles - Sobreajuste

47. Implementando árboles - Sobreajuste
 C4.5 implementa un algoritmo de post-poda basado en la
tasa de aciertos del nivel en el cual está evaluando
comparado con el que tendría si abre el nodo.
 En cada nodo, el algoritmo compara:
 el error ponderado de cada nodo hijo con
 el error de la clasificación si se suprimen los nodos hijos y se lo etiqueta
con la clase mayoritaria.

48. Implementando árboles - Sobreajuste
 TreeGrowing (S,A,y,SplitCriterion,StoppingCriterion)
 Where:
 S - Training Set
 A - Input Feature Set
 y - Target Feature
 SplitCriterion --- the method for evaluating a certain split
 StoppingCriterion --- the criteria to stop the growing process
 Create a new tree T with a single root node.

49. Implementando árboles - Sobreajuste
 Algunos métodos de poda:
 Cost Complexity Pruning (CP)
 Reduced Error Pruning (REP)
 Minimum Error Pruning (MEP)
 Pessimistic Pruning (PP)
 Error Based Pruning (EBP)
 Minimum Description Length Pruning (MDL)

50. Implementando árboles - Discretización
En aprendizaje supervisado, la mejor
discretización es aquella que produce el mejor
resultado para el modelo que será utilizado para
predecir.

51. Implementando árboles - Discretización
Example: attribute temperature.
1) Order all values in the training set
2) Consider only those cut points where there is a change of class
3) Choose the cut point that maximizes information gain
temperature
97 97.5 97.6 97.8 98.5 99.0 99.2 100 102.2 102.6 103.2

52. Implementando árboles - Discretización
 Decidir cuántas categorías usar:
 Dividir en N intervalos con N-1 puntos de split
 Decidir dónde colocarlos
 Determinar cómo mapear los valores del atributo
continuo a estas categorías.

53. Implementando árboles - Discretización
 Métodos No Supervisados (no utiliza información de la
clase)
 Equal Width (Top-Down)
 Equal Frequency (Top-Down)
 Clustering por K-medias (Bottom-Up)
 Inspección visual de los datos y Particionamiento Natural
 Métodos Supervisados (utiliza información de la clase)
 Enfoque Estadístico (Bottop – Up)
 Enfoque basado en la Entropía

54. Implementando árboles - Discretización
 Permiten reducir los datos al reemplazar conceptos de
bajo nivel (ej: valores numéricos de la edad) por
conceptos de alto nivel (ej: joven, adulto, ansiano).
 Pueden existir más de una jerarquía para un mismo
atributo.
 Los atributos con conceptos tienden a ser más representativos de
lo que intentan mostrar y son más faciles de interpretar aunque
se pierde algo de información.

55. Implementando árboles – Discretización - Jerarquías

56. Implementando árboles – Discretización - Binning
 Equal Width Binning:
 divide el rango de atributos en N intervalos de la misma longitud.
 Ventajas: sencillo de aplicar
 Desventajas: se ve afectado por outliers; las instancias se distribuyen
de manera desigual.
 Equal Frequency Binning:
 divide el rango de atributos en N intervalos basados en la
distribución de las instancias. El objetivo es poner la misma
cantidad de instancias en cada intervalo.
 Ventajas: obtiene buenos resultados en conjunción con el método de
aprendizaje Naïve Bayes.
 Desventajas: al ser ajeno a las clases de las instancias puede resultar
en intervalos pobres.

57. Implementando árboles - Discretización
 K-Means:
 define un prototipo en términos de un centroide que es
usualmente la media de un grupo de puntos y es aplicado a
objets en un espacio contínuo n-dimensional.

58. Implementando árboles – Valores faltantes en atributos
 Hay varias aproximaciones:
 Ignorarlos.
 Buscar algoritmos que los acepten.
 Completarlos:
 Valor más común o promedio.
 ¿Uso la clase o no?
 ¿Miro todo el conjunto o el subconjunto?
 ¿Si elraboro un método de clasificación utilizando el atributo con
datos faltantes como clase?
 ¿Si genero y testeo?

59. Analytics – Árboles de decisión
 ¿Induciendo árboles?
 Implementando árboles
 Criterio de selección
 Criterio de parada
 Sobreajuste
 Valores numéricos
 Valores faltantes
 “Árboles se buscan”
 ¿Árboles o bosques?

60. Árboles de decisión – Búsqueda heurística

61. Árboles de decisión – Búsqueda heurística

62. ¿y ahora?
 We search over the hypothesis space of all possible decision trees.
 We keep only one hypothesis at a time, instead of having several.
 We don’t do backtracking in the search. We choose the best alternative
and continue growing the tree.
 We prefer shorter trees than larger trees.
 We prefer trees where attributes with lowest entropy are placed on the top.
Enfoque tradicional …

63. Árboles de decisión – Búsqueda heurística

64. Analytics – Árboles de decisión
 ¿Induciendo árboles?
 Implementando árboles
 Criterio de selección
 Criterio de parada
 Sobreajuste
 Valores numéricos
 Valores faltantes
 “Árboles se buscan”
 ¿Árboles o bosques?

65. ¿y ahora?
¿Árboles o bosques?

66. ¿y ahora?
¿Hago muchas cuentas
o genero y pruebo?

67. ¿y ahora?
¿Cuánto arriesgo?

68. eduardopoggi@yahoo.com.ar
eduardo-poggi
http://ar.linkedin.com/in/eduardoapoggi
https://www.facebook.com/eduardo.poggi
@eduardoapoggi

69. Bibliografía