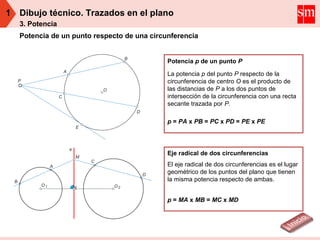
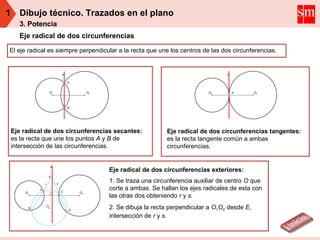
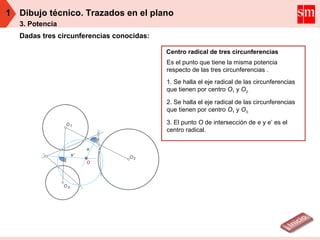
El documento explica conceptos geométricos relacionados con la potencia de puntos respecto a circunferencias. Define la potencia de un punto como el producto de las distancias del punto a los puntos de intersección de una circunferencia con una recta secante. Explica que el eje radical de dos circunferencias es el lugar geométrico de los puntos que tienen la misma potencia respecto a ambas, y cómo calcular el eje radical para circunferencias secantes, tangentes o exteriores. También define el centro radical de tres circunferencias como el

1. Dibujo técnico. Trazados en el plano
3. Potencia
1

2. Dibujo técnico. Trazados en el plano
3. Potencia
Potencia de un punto respecto de una circunferencia
1
A
C
E
O
B
D
P
e
B
D
A
M
C
O O21
Potencia p de un punto P
La potencia p del punto P respecto de la
circunferencia de centro O es el producto de
las distancias de P a los dos puntos de
intersección de la circunferencia con una recta
secante trazada por P.
Eje radical de dos circunferencias
El eje radical de dos circunferencias es el lugar
geométrico de los puntos del plano que tienen
la misma potencia respecto de ambas.
p = PA x PB = PC x PD = PE x PE
p = MA x MB = MC x MD

3. Dibujo técnico. Trazados en el plano
3. Potencia
Eje radical de dos circunferencias
1
e
2OO1
B
e
O1 O2A
e
sr
E
O
1O 2O
A
Eje radical de dos circunferencias secantes:
es la recta que une los puntos A y B de
intersección de las circunferencias.
El eje radical es siempre perpendicular a la recta que une los centros de las dos circunferencias.
Eje radical de dos circunferencias tangentes:
es la recta tangente común a ambas
circunferencias.
Eje radical de dos circunferencias exteriores:
1. Se traza una circunferencia auxiliar de centro O que
corte a ambas. Se hallan los ejes radicales de esta con
las otras dos obteniendo r y s.
2. Se dibuja la recta perpendicular a O1O2 desde E,
intersección de r y s.
A
B
D
C

4. Dibujo técnico. Trazados en el plano
3. Potencia
Dadas tres circunferencias conocidas:
1
e'
e
O3
2O
O1
O
Centro radical de tres circunferencias
Es el punto que tiene la misma potencia
respecto de las tres circunferencias .
1. Se halla el eje radical de las circunferencias
que tienen por centro O1 y O2.
2. Se halla el eje radical de las circunferencias
que tienen por centro O1 y O3.
3. El punto O de intersección de e y e’ es el
centro radical.