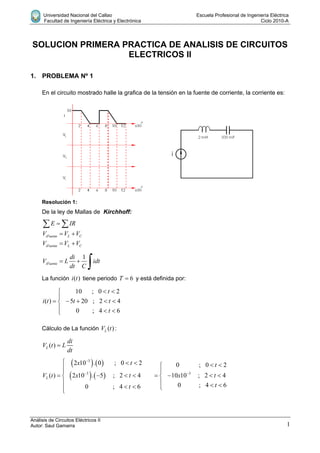
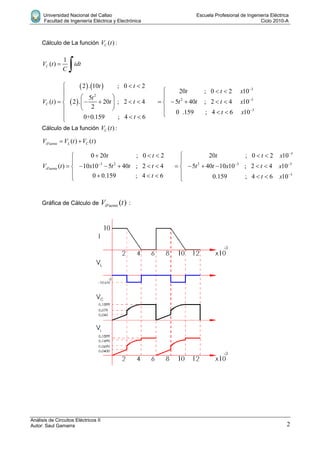
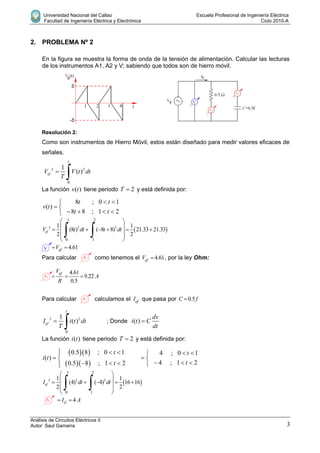
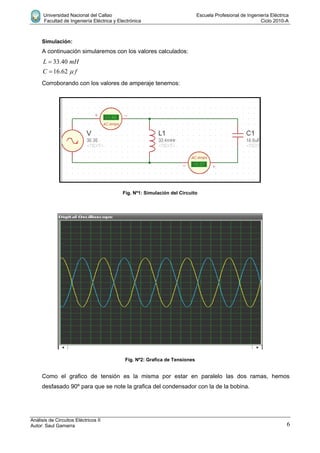
Este documento presenta la resolución de 4 problemas de circuitos eléctricos. El primer problema involucra calcular la corriente y tensión en un circuito RC. El segundo calcula las lecturas de instrumentos de medición para una onda de tensión dada. El tercer problema determina los valores de inductancia y capacitancia para un circuito LC en paralelo. El cuarto problema calcula la frecuencia a la que la corriente se adelanta 30 grados respecto a la tensión en un circuito RC en serie.

1. Universidad Nacional del Callao Escuela Profesional de Ingeniería Eléctrica
Facultad de Ingeniería Eléctrica y Electrónica Ciclo 2010-A
Análisis de Circuitos Eléctricos II
Autor: Saul Gamarra 1
SOLUCION PRIMERA PRACTICA DE ANALISIS DE CIRCUITOS
ELECTRICOS II
1. PROBLEMA Nº 1
En el circuito mostrado halle la grafica de la tensión en la fuente de corriente, la corriente es:
Resolución 1:
De la ley de Mallas de Kirchhoff:
E IR 
iFuente L CV V V 
iFuente L CV V V 
1
iFuente
di
V L idt
dt C
 

La función ( )i t tiene periodo 6T  y está definida por:
10 ; 0 2
( ) 5 20 ; 2 4
0 ; 4 6
t
i t t t
t
 

    
  
Cálculo de La función ( )LV t :
( )L
di
V t L
dt

   
   
3
3 3
2 10 . 0 ; 0 2 0 ; 0 2
( ) 2 10 . 5 ; 2 4 10 10 ; 2 4
0 ; 4 60 ; 4 6
L
x t t
V t x t x t
tt

 
    

        
     

2. Universidad Nacional del Callao Escuela Profesional de Ingeniería Eléctrica
Facultad de Ingeniería Eléctrica y Electrónica Ciclo 2010-A
Análisis de Circuitos Eléctricos II
Autor: Saul Gamarra 2
Cálculo de La función ( )CV t :
1
( )CV t idt
C


   
 
3
2
2 3
2 . 10 ; 0 2
20 ; 0 2 10
5
( ) 2 . 20 ; 2 4 5 40 ; 2 4 10
2
0 .15
0+0.159 ; 4 6
C
t t
t t x
t
V t t t t t t x
t


 
 
 
           
 
  
3
9 ; 4 6 10t x 



  
Cálculo de La función ( )CV t :
( ) ( )iFuente L CV V t V t 
3
3 2 2
0 20 ; 0 2 20 ; 0 2 10
( ) 10 10 5 40 ; 2 4 5 40 10
0 0.159 ; 4 6
iFuente
t t t t x
V t x t t t t t
t


    

         
   
3 3
3
10 ; 2 4 10
0.159 ; 4 6 10
x t x
t x
 



 
  
Gráfica de Cálculo de ( )iFuenteV t :

3. Universidad Nacional del Callao Escuela Profesional de Ingeniería Eléctrica
Facultad de Ingeniería Eléctrica y Electrónica Ciclo 2010-A
Análisis de Circuitos Eléctricos II
Autor: Saul Gamarra 3
2. PROBLEMA Nº 2
En la figura se muestra la forma de onda de la tensión de alimentación. Calcular las lecturas
de los instrumentos A1, A2 y V; sabiendo que todos son de hierro móvil.
Resolución 2:
Como son instrumentos de Hierro Móvil, estos están diseñado para medir valores eficaces de
señales.
2 2
0
1
( )ef
t
V V t dt
T


La función ( )v t tiene periodo 2T  y está definida por:
8 ; 0 1
( )
8 8 ; 1 2
t t
v t
t t
 
 
   
 2 2 2
1 2
0 1
1 1
(8 ) ( 8 8) 21.33 21.33
2 2
efV t dt t dt
 
      
 
 
 
 
4.61efV 
Para calcular como tenemos el 4.61efV  , por la ley Ohm:
4.61
9.22
0.5
efV
A
R
  
Para calcular calculamos el efI que pasa por 0.5C f
2 2
0
1
( )ef
t
I i t dt
T

 ; Donde ( )
dv
i t C
dt

La función ( )i t tiene periodo 2T  y está definida por:
  
  
0.5 8 ; 0 1 4 ; 0 1
( )
4 ; 1 20.5 8 ; 1 2
t t
i t
tt
   
  
     
 2 2 2
1 2
0 1
1 1
(4) ( 4) 16 16
2 2
efI dt dt
 
     
 
 
 
 
4efI A 

4. Universidad Nacional del Callao Escuela Profesional de Ingeniería Eléctrica
Facultad de Ingeniería Eléctrica y Electrónica Ciclo 2010-A
Análisis de Circuitos Eléctricos II
Autor: Saul Gamarra 4
3. PROBLEMA Nº 3
Un circuito Paralelo L-C tiene aplicada una tensión de 50cos(3000 45)V t  y la intensidad
de corriente es 2cos(3000 45)i t  . La corriente en la rama capacitiva es 5 veces mayor que
la de la rama inductiva. Hallara L y C
Resolución 3:
Tenemos de datos:
50cos(3000 45)V t 
2cos(3000 45)i t 
5c LI I
50
45
2
V  
2
45
2
i 
Sabemos que:
eqV iZ
Donde:
  
 
L C L C
eq
L C L C
jX jX X X
Z j
j X X X X

  
 
Reemplazando que:
50
45
2 25 90 25cos( 90) 25 ( 90)
2
45
2
eqZ j sen

      
25eqZ j 

5. Universidad Nacional del Callao Escuela Profesional de Ingeniería Eléctrica
Facultad de Ingeniería Eléctrica y Electrónica Ciclo 2010-A
Análisis de Circuitos Eléctricos II
Autor: Saul Gamarra 5
Igualando que:
25L C
L C
X X
X X


Dato que: 5c LI I
50
45
502 135
90 2
L L L
L L
L
V i Z i
X X
i

    

50
45
502 45
90 2
C C C
C C
C
V i Z i
X X
i

   


50 50
5
2 2
L C
C L
X X
X X
  
2
5
25
4
C
C
X
X

Nos queda: 5c LI I
20
100
C
L
X
X


LX L
1
Xc
C

3000 
33.40
16.62
L mH
C f



6. Universidad Nacional del Callao Escuela Profesional de Ingeniería Eléctrica
Facultad de Ingeniería Eléctrica y Electrónica Ciclo 2010-A
Análisis de Circuitos Eléctricos II
Autor: Saul Gamarra 6
Simulación:
A continuación simularemos con los valores calculados:
33.40
16.62
L mH
C f


Corroborando con los valores de amperaje tenemos:
Fig. Nº1: Simulación del Circuito
Fig. Nº2: Grafica de Tensiones
Como el grafico de tensión es la misma por estar en paralelo las dos ramas, hemos
desfasado 90º para que se note la grafica del condensador con la de la bobina.

7. Universidad Nacional del Callao Escuela Profesional de Ingeniería Eléctrica
Facultad de Ingeniería Eléctrica y Electrónica Ciclo 2010-A
Análisis de Circuitos Eléctricos II
Autor: Saul Gamarra 7
4. PROBLEMA Nº 4
Un circuito serie se compone de una resistencia 8R   y un condensador con una
capacidad de 30C f . ¿A qué frecuencia la corriente adelanta un ángulo de 30º respecto
de la tensión? En Hz
Resolución 4:
Por el triangulo de impedancias.
tan
Xc
R
  ;
1
Xc
C

1
tan30
CR
 ; 2 f 
1
tan30
2 fCR

1
2 tan30
f
fCR

  6
1
2 30 10 8 tan30
f
x 

1148.6f Hz

8. Universidad Nacional del Callao Escuela Profesional de Ingeniería Eléctrica
Facultad de Ingeniería Eléctrica y Electrónica Ciclo 2010-A
Análisis de Circuitos Eléctricos II
Autor: Saul Gamarra 8
Simulación:
A continuación simularemos con una tensión AC de 25V, 1148.6f Hz que es la calculada
Fig. Nº3: Simulación del Circuito
Fig. Nº4: Grafica de Tensiones