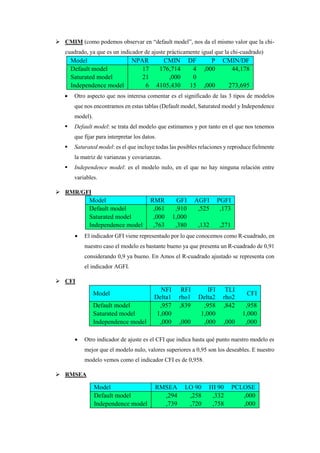
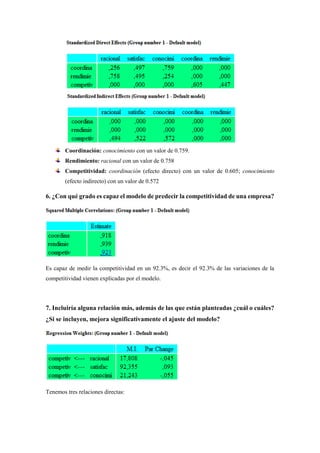
El análisis de caminos (path analysis) se utiliza para representar y medir las interdependencias entre variables a través de un modelo de regresión que establece relaciones causales. En un estudio de mercado de 500 empresas, se evaluaron variables como el conocimiento de los directivos, la satisfacción laboral y el rendimiento, encontrando que estos influyen sobre la competitividad empresarial, la cual puede ser predecida en un 92.3% por el modelo. Se sugiere que agregar relaciones adicionales entre variables puede mejorar significativamente el ajuste del modelo.

1. PATH ANALYSIS
GMIM, 3ºA
Cruz Galvín, Carlos
Mingorance Fernández, Jonathan
Trueba Moreno, Javier

2. Introducción
o El análisis del camino (Path analysis) o análisis de pautas es un análisis de regresión
múltiple más un diagrama de flujo de las interdependencia. Es una aplicación de la
inferencia estadística y la teoría de grafos. Primero se determina el orden de las
dependencias o prioridades entre variables por una Encuesta, por un método intuitivo u
otro método.
o Hecha la selección se analiza este material con Tablas de contingencia y Matriz de
correlación y el análisis medirá los caminos críticos con valores esperados o reales. Es un
test que puede fallar si no se establece racionalmente el orden de las dependencias en la
red del modelo causal, se emplean variables no relevantes y no se cumplen los supuestos
básicos.
o Un ejemplo puede ser las influencias de la educación y los ingresos de los padres en los
hábitos de lectura y compra de libros de los hijos. Se dibuja una gráfica con todas las
posibles rutas, que en la forma más simple tomará la apariencia en estrella de un triángulo
con una Y inscrita entre sus vértices.
o Los vectores resultarán bidireccionales <--> cuando no se supo o pudo establecer
dependencias -educación/ingresos- y en los otros casos positivos, estarán orientados en
la dirección causa --> efecto <-- causa con sus correspondientes índices cuantitativos de
la Tabla de regresión -hábitos/compra-. La principal propiedad es que el modelo es más
expresivo que una tabla, como era de esperar cuando se recurre a un método grafico para
análisis multivariable. Las rutas de tráfico se pueden establecer como ecuaciones
estructurales lineales de coeficientes de camino.

3. DETERMINANTES DE LA COMPETITIVIDAD DE LA
EMPRESA
BD: Base práctica Tema 4
SUPONGAMOS QUE SE LLEVA A CABO UN ESTUDIO DE MERCADO EN EL QUE SE
LES PREGUNTA A 500 EMPRESAS POR SEIS CUESTIONES MEDIDAS EN UNA ESCALA
CUYOS EXTREMOS SON 0 Y 11:
Variables
- CONOCIMIENTOS DE SUS DIRECTIVOS (CONOCIMI) SOBRE LOS PRODUCTOS QUE
VENDE LA EMPRESA, LOS CANALES DE DISTRIBUCIÓN QUE USA, DIRECCIÓN
ESTRATÉGICA Y RECURSOS HUMANOS, ENTRE OTRAS CUESTIONES. PARA ELLO SE
EMPLEA UNA ESCALA FORMADA POR VEINTE PREGUNTAS. SE SUMAN LAS
PUNTUACIONES DE TODAS ESTAS PREGUNTAS Y SE CALCULA SU MEDIA.
- SATISFACCIÓN CON EL TRABAJO QUE REALIZAN EN LA EMPRESA (SATISFAC).
PARA ELLO SE EMPLEAN CINCO CUESTIONES. SE SUMAN SUS PUNTUACIONES Y SE
CALCULA LA MEDIA.
- TENDENCIA A EVALUAR DE FORMA RACIONAL (RACIONAL) LAS DECISIONES
QUE TOMAN PARA ALCANZAR UN FIN U OBJETIVO. PARA ELLO SE USA UNA
ESCALA FORMADA POR DIECIOCHO CUESTIONES. SE SUMAN SUS PUNTUACIONES
Y SE CALCULA UNA MEDIA.
- RENDIMIENTO DEL DIRECTIVO (RENDIMIE). SE USAN VEINTICUATRO
CUESTIONES PARA EVALUAR EL RENDIMIENTO RELACIONADO CON LA
PLANIFICACIÓN, ORGANIZACIÓN, CONTROL, COORDINACIÓN DEL
DEPARTAMENTO DONDE TRABAJA Y DIRECCIÓN. SE SUMAN LAS PUNTUACIONES
OBTENIDAS EN CADA UNO DE LOS ÍTEMS Y SE CALCULA UNA MEDIA.
- COORDINACIÓN CON OTROS DEPARTAMENTOS (COORDINA). TRECE
PREGUNTAS PARA EVALUAR COMO EL DEPARTAMENTO DEL DIRECTIVO ESTÁ
COORDINADO CON OTROS DEPARTAMENTOS. SE SUMAN LAS PUNTUACIONES Y
SE CALCULA UNA MEDIA.
- LA COMPETITIVIDAD DE LA EMPRESA (COMPETIV). SE USAN CUATRO
CUESTIONES QUE TIENEN QUE VER CON LOS RESULTADOS OBTENIDOS POR LA
EMPRESA, LA CUOTA DE MERCADO QUE TIENE Y EL ROL QUE JUEGA EN EL
MERCADO (LÍDER, SEGUIDOR, IMITADOR). IGUAL QUE EN LAS CINCO
CUESTIONES ANTERIORES, SE SUMARON LAS PUNTUACIONES DADAS Y SE
CALCULÓ UNA MEDIA.

4. Enunciado
Según la teoría revisada, se conoce que:
1. El conocimiento de los directivos, la satisfacción con el trabajo y la tendencia a evaluar de
forma racional influyen tanto sobre el rendimiento del directivo como en la coordinación
con otros departamentos.
2. El rendimiento del directivo y la coordinación con otros departamentos influyen sobre la
competitividad de la empresa.
Se pide contestar a los siguientes apartados
1.- Plantear el Path Diagram
2.- Evalúe el ajuste global del modelo planteado estimado por máxima verosimilitud
Chi-cuadrado: 176,714 p-value: 0,000
Ho: la matriz de varianzas covarianzas estimada es igual que la observada
H1: la matriz de varianzas covarianzas estimada es diferente que la observada (En este caso
rechazamos la hipótesis nula)
- Este valor está afectado por un gran nº de casos existentes en torno a 500 y podemos decir que
cuando es superior a 200 el valor de la chi-cuadrado aumenta sensiblemente con el tamaño
muestral.
- A continuación representamos un conjunto de indicadores que nos servirán para observar el
ajuste global del modelo.

5.  CMIM (como podemos observar en “default model”, nos da el mismo valor que la chi-
cuadrado, ya que es un indicador de ajuste prácticamente igual que la chi-cuadrado)
 Otro aspecto que nos interesa comentar es el significado de las 3 tipos de modelos
que nos encontramos en estas tablas (Default model, Saturated model y Independence
model).
 Default model: se trata del modelo que estimamos y por tanto en el que nos tenemos
que fijar para interpretar los datos.
 Saturated model: es el que incluye todas las posibles relaciones y reproduce fielmente
la matriz de varianzas y covarianzas.
 Independence model: es el modelo nulo, en el que no hay ninguna relación entre
variables.
 RMR/GFI
 El indicador GFI viene representado por lo que conocemos como R-cuadrado, en
nuestro caso el modelo es bastante bueno ya que presenta un R-cuadrado de 0,91
considerando 0,9 ya bueno. En Amos el R-cuadrado ajustado se representa con
el indicador AGFI.
 CFI
 Otro indicador de ajuste es el CFI que indica hasta qué punto nuestro modelo es
mejor que el modelo nulo, valores superiores a 0,95 son los deseables. E nuestro
modelo vemos como el indicador CFI es de 0,958.
 RMSEA
Model NPAR CMIN DF P CMIN/DF
Default model 17 176,714 4 ,000 44,178
Saturated model 21 ,000 0
Independence model 6 4105,430 15 ,000 273,695
Model RMR GFI AGFI PGFI
Default model ,061 ,910 ,525 ,173
Saturated model ,000 1,000
Independence model ,763 ,380 ,132 ,271
Model
NFI
Delta1
RFI
rho1
IFI
Delta2
TLI
rho2
CFI
Default model ,957 ,839 ,958 ,842 ,958
Saturated model 1,000 1,000 1,000
Independence model ,000 ,000 ,000 ,000 ,000
Model RMSEA LO 90 HI 90 PCLOSE
Default model ,294 ,258 ,332 ,000
Independence model ,739 ,720 ,758 ,000

6.  El último indicador es el RMSEA, que indica la parte de la matriz de varianzas y
covarianzas observada que no es capaz de explicar nuestro modelo algo parecido
a los residuos lo que no soy capaz de explicar con las variables independientes,
lo que quiero es que sea cercana a 0 considerándolas como valores favorables,
siguiendo valores inferiores a 0,08. Pero en nuestro modelo el valor RMSEA es
de 0,294 no estando cerca de 0 o 0,08.
3.- Comprobar si las variables utilizadas siguen una distribución normal, así como
si todas ellas siguen una distribución normal multivariante (al menos, en cuanto a
curtosis).
- La asimetría (skew) la analizamos entre ciertos valores cercanos a 0, podemos decir que se
encuentran próximos a 0 por lo que el modelo es relativamente simétrico. Esta conclusión la
contrastamos a través de su ratio crítico (c.r) en la que observamos que todos los valores se
encuentran en la zona de aceptación (-1,96 y 1,96)
- En cuanto a curtosis (Kurtosis) aunque deba centrase en torno a 3, el programa lo estandariza
entre valores (0, 1) siendo necesario observar el ratio crítico (c.r), en el que todos los valores se
encuentran en torno a (-1,96 y 1.96) en la zona de aceptación. Al estandarizar, el valor en el cual
la distribución es mesocúrtica, es 0.
- Respecto a la multivariante, en su conjunto es normal, como podemos ver en su valor crítico que
es -0.363; estando la región crítica, en la zona de aceptación (-1,96 y 1,96)

7. 4. Analizar los coeficientes no estandarizados que se obtienen.
 Un aumento en una unidad del “conocimiento” produce un aumento del rendimiento en
0.219.
 Un aumento en una unidad de la “satisfacción” produce un aumento en el rendimiento de
0.348
 Un aumento en una unidad de la “satisfacción” produce un aumento sobre la coordinación
de 0.325
 Un aumento en una unidad de la “tendencia a evaluar de forma racional” produce un
aumento en la coordinación de 0.186
 Un aumento en una unidad del “conocimiento” produce un aumento en la coordinación
de 0.609
 Un aumento en una unidad de la “tendencia a evaluar de forma racional” produce un
aumento en el rendimiento de 0.590
 Un aumento en una unidad del “rendimiento” produce un aumento en la competitividad
de 0.494
 Un aumento en una unidad de la “coordinación” produce un aumento en la competitividad
de 0.719
5. Indicar el determinante principal de cada variable endógena del modelo.
Justifique su respuesta. Tenga en cuenta que hay tanto efectos directos como
indirectos.

8. Coordinación: conocimiento con un valor de 0.759.
Rendimiento: racional con un valor de 0.758
Competitividad: coordinación (efecto directo) con un valor de 0.605; conocimiento
(efecto indirecto) con un valor de 0.572
6. ¿Con qué grado es capaz el modelo de predecir la competitividad de una empresa?
Es capaz de medir la competitividad en un 92.3%, es decir el 92.3% de las variaciones de la
competitividad vienen explicadas por el modelo.
7. Incluiría alguna relación más, además de las que están planteadas ¿cuál o cuáles?
¿Si se incluyen, mejora significativamente el ajuste del modelo?
Tenemos tres relaciones directas:

9. 1. Relación directa entre racional y competitividad: si incluimos esta la chi-cuadrado bajará
como mínimo en 17.808 y su coeficiente estará en torno a -0.045.
2. Relación directa entre satisfacción y competitividad: si incluimos esta la chi-cuadra bajará
como mínimo en 92.355 (una cuantía muy importante o destacable) y su coeficiente va a
rondar en 0.93.
3. Relación directa entre conocimiento y competitividad: si incluimos esta relación la chi-
cuadrado se reducirá como mínimo en 21,243 y su coeficiente girara en torno a -0.055.
Vamos a comparar el ajuste entre ambos modelos:
Chi-square = 176,714
Degrees of freedom = 4
Probability level = ,000
LR= 176.714-0.001=176.715  Chi-cuadrado1= 2.52758e-040
Podemos afirmar que el ajuste es significativamente mejor en nuestro último modelo, en el que
hemos añadido las relaciones directas anteriores.
Chi-square = ,001
Degrees of freedom = 1
Probability level = ,975