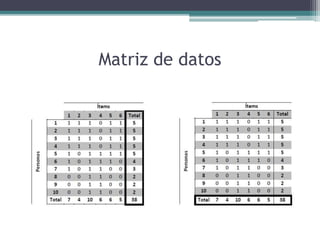
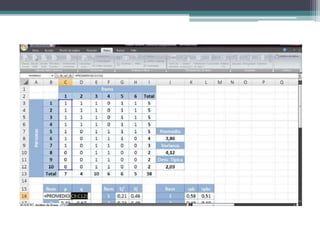
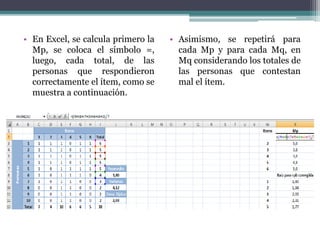
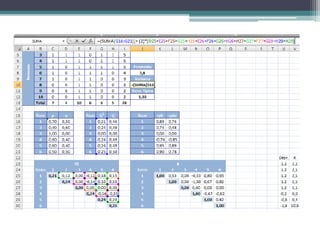
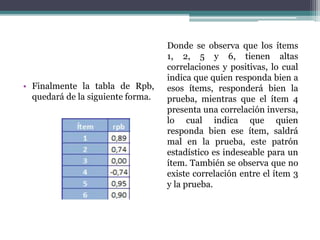
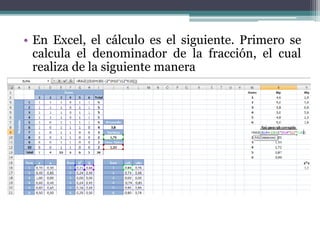
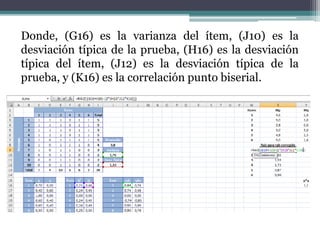
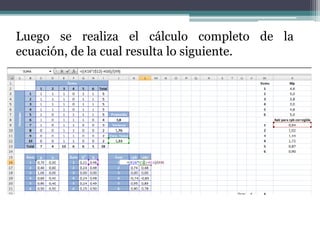
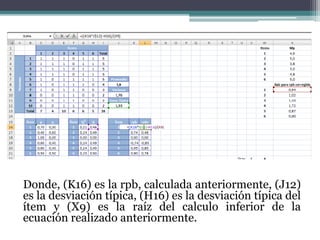
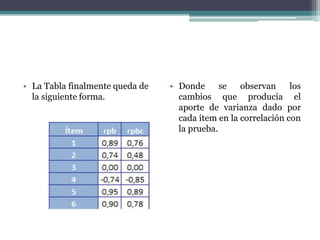
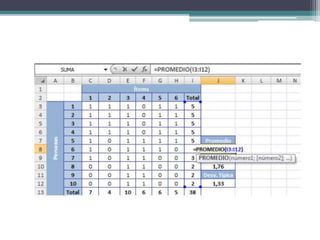
El documento presenta el análisis psicométrico de 6 ítems de una prueba a la que respondieron 10 personas. Se calculan los índices de dificultad, varianza y desviación estándar de cada ítem para evaluar su capacidad discriminativa. El ítem 3 muestra nula capacidad y debería eliminarse. También se calcula la correlación punto-biserial corregida de cada ítem con la prueba total para evaluar su validez de constructo.

1. ANALISIS DE ITEMS
Introducción a la Psicometría
Profesor: José Antonio Calvo

2. Items
• Los ítems son los que permiten la medición, según
Tavella y Sánchez (2001), el ítem se compone de la
situación o problema y de las respuestas al mismo.
• En el caso que nos ocupa, se realizará el análisis de
ítems binarios, es decir, de ítems que solo tienen
una respuesta correcta, la cual tendrá un valor de
uno (1) y una respuesta o varias incorrectas que
tendrán el valor de cero (0).

3. Matriz de Datos
• Se les administro una prueba
de seis (6) ítems a diez (10)
personas y los resultados
fueron los presentados
anteriormente

4. Matriz de datos

5. Índice de dificultad
• Para comenzar a realizar el
análisis lo primero que hay
que buscar es la p del ítem o
dificultad del mismo, la
dificultad se encuentra como
la proporción de personas que
contestaron correctamente el
ítem, en Excel esto se realiza
colocándose en una celda
inferior de total de esa casilla,
allí se coloca un signo de
igualdad (=), seguido de la
palabra promedio, como se
muestra a continuación:

6. Índice de dificultad
• Luego, se coloca inmediatamente un paréntesis y
se toma con el mouse la columna del primer
ítem obviando el valor del total, como se
muestra a continuación. Cierra el paréntesis y al
darle a la tecla ENTER para finalizar, así se
realizará con cada columna de ítems

8. Índice de dificultad
Luego de lo anterior, se calculará la q del ítem, la
cual es la proporción de personas que responden
incorrectamente el ítem, esto se realiza, en la
celdas continuas a donde se realizo el calculo de p
de ítem. Lo que se hará es que se coloca el signo de
igualdad (=), se abre un paréntesis ((), y dentro
del mismo se coloca un uno (1) y se le resta la
celda de la primera p del ítem, luego se cierra el
paréntesis ()), finalizando se le da a la tecla
ENTER. Como se muestra a continuación

9. Índice de dificultad
• Para no tener que repetir lo mismo con
cada columna de ítems, lo recomendable
es tomar con el mouse y la cruz negra (+)
que aparece al colocarse en la esquina
inferior derecha de la celda que se acaba
de realizar y esto se estira, hasta el ítem
numero seis (6), como se muestra a
continuación:

10. Índice de dificultad
• La p, inferior a 0,20 serán ítems difíciles y los
superiores serán ítems entre regular y fácil de
responder, al tener una p igual a 1 indicará que
el ítem es contestado por todas las personas, y si
es cero (0), nadie contesta ese ítem, es decir
ambos deberán ser descartados. En el caso
anterior, el ítem 3 deberá según esto ser
eliminado o pasar a evaluación, porque se
observa que tiene un p =1, lo cual indica que es
contestado por todas las personas, es decir es un
ítem fácil.

11. Varianza y desviación del ítem
• varianza del ítem indica la
capacidad discriminativa del
ítem, es decir, colabora con la
visión que se tiene de si el ítem
detecta las diferencias
individuales de la variable a
medir. La Varianza se calcula
multiplicando p *q= Sj2.
• Los puntajes entre los cuales
se puede encontrar la varianza
son un mínimo de cero (0) y
un máximo de veinticinco
decimas (0,25), lo cual
indicará si es cero que no tiene
capacidad discriminativa y si
es de 0,25 tendrá una alta
capacidad discriminativa.

12. Varianza y desviación del ítem
• En Excel, esto se calcula
colocándose en otra celda
continua a donde se calculo p
y q. Allí se coloca el signo de
igualdad (=), seguido de un
paréntesis ((), luego se coloca
la celda de donde se calculo p
y se coloca el signo de
multiplicación (*), paso
seguido se coloca la celda
donde se calculo q, y se cierra
el paréntesis ()) y se teclea
ENTER. Como se muestra a
continuación :

13. Varianza y desviación del ítem
• Para finalizar se realiza lo
mismo que se hizo con la q del
ítem, se arrastrará el mouse y
la cruz negra (+) que aparece
al colocarse en la esquina
inferior derecha de la celda
que se acaba de realizar hasta
el ítem numero seis (6), como
se muestra a continuación:

14. Varianza y desviación del ítem
• La desviación del ítem se
calcula hallando la raíz
cuadrada de la varianza del
ítem. Es decir la formula seria
la siguiente:
• En Excel, esto se calcula
colocándose en la celda
contigua a donde se calculó
Sj2, se inicia con el signo de
igualdad (=), luego la palabra
RAIZ, y se coloca entre
paréntesis (()) la celda de Sj2,
y se presiona la tecla ENTER,
como se muestra a
continuación:

15. Varianza y desviación del ítem

16. Varianza y desviación del ítem
• Para finalizar se realiza lo
mismo que se hizo con la q del
ítem, se arrastrará el mouse y
la cruz negra (+) que aparece
al colocarse en la esquina
inferior derecha de la celda
que se acaba de realizar hasta
el ítem numero seis (6), como
se muestra a continuación:

17. Varianza y desviación del ítem
• Los valores entre los que oscila la desviación del
ítem, es entre cero (0) y cincuenta decimas,
(0,50), lo cual indica que si está cercano a cero
(0), no tiene capacidad discriminativa y si está
cercano a 0,50 tiene una alta capacidad
discriminativa.

18. Varianza y desviación del ítem
El análisis de la capacidad discriminativa de los ítems de la
prueba que se está evaluando, muestra que el ítem 3
demuestra una nula capacidad discriminativa, ya que es de
cero (0), aunado esto a que se mostraba como un ítem
fácil, porque todas las personas lo respondían, se está
mostrando como un ítem que debería ser eliminado de la
prueba, los demás ítems tienen una buena capacidad
discriminativa, ya que se encuentran cercanos a 0,25 en
varianza y 0,50 en desviación, se puede decir también, que
el ítem 6 tiene una dificultad media, ya que es de 0,50 y
una alta capacidad discriminativa ya que tiene los mayores
valores de varianza y desviación (0,25-0,50)
respectivamente

19. Correlación punto biseral
• Es conocida también como
correlación ítem-prueba,
donde se informa la relación
existente entre un ítem binario
y las calificaciones totales de la
prueba.
• La formula empleada para su
cálculo es la siguiente:
donde Mp es la media de las
calificaciones de las personas
que responden bien el ítem, y la
Mq, es la media de las
calificaciones de las personas
que lo responden mal, St es la
desviación de la distribución de
puntajes de la prueba y Sj es la
del ítem que se estudia.

20. • En Excel, se calcula primero la
Mp, se coloca el símbolo =,
luego, cada total, de las
personas que respondieron
correctamente el ítem, como se
muestra a continuación.
• Asimismo, se repetirá para
cada Mp y para cada Mq, en
Mq considerando los totales de
las personas que contestan
mal el ítem.

21. La varianza total de la prueba implica la
dispersión de los puntajes con respecto a la media
de la prueba, de ser 0 no hay dispersión entre los
mismos, siendo mayor se podrá dar mayor
información acerca de lo que sucede con las
puntuaciones. La varianza depende de las
varianzas de los ítems, y se calcula de la siguiente
forma
luego se le saca la raíz cuadrada y se obtiene la
desviación típica de la prueba lo cual en Excel, se
realiza de la siguiente forma.

23. • La sumatoria inicial, es la de
las varianzas de cada ítem, así
como luego se suma cada
covarianza para esto ser
multiplicado por la constante
2. Luego para encontrar la
raíz, se sitúa en otra celda, se
coloca =Raíz (la celda donde
se encuentre la varianza) y
listo.
• Luego de cada cálculo, se sitúa
en otra celda, donde se realiza
la formula de Rpb, como se
muestra a continuación.

24. Se observa que (X2) es la Mp del ítem 1, (Y2) es la
celda de Mq, (J12) es la desviación típica de la
prueba total y (H16) es la desviación típica del
ítem.

25. • Finalmente la tabla de Rpb,
quedará de la siguiente forma.
Donde se observa que los ítems
1, 2, 5 y 6, tienen altas
correlaciones y positivas, lo cual
indica que quien responda bien a
esos ítems, responderá bien la
prueba, mientras que el ítem 4
presenta una correlación inversa,
lo cual indica que quien
responda bien ese ítem, saldrá
mal en la prueba, este patrón
estadístico es indeseable para un
ítem. También se observa que no
existe correlación entre el ítem 3
y la prueba.

26. • Cuando una prueba esta
compuesta por pocos
reactivos, como en la actual, la
correlación ítem-prueba se ve
sobreestimada, entonces se
recomienda aplicar la ecuación
de la correlación Rpb
corregida o Rpb-1, la cual es
• la información que dan ambas
correlaciones es la misma, solo
que su diferencia radica en que
dependerá del numero de
reactivos que tenga la prueba.

27. • En Excel, el cálculo es el siguiente. Primero se
calcula el denominador de la fracción, el cual
realiza de la siguiente manera

28. Donde, (G16) es la varianza del ítem, (J10) es la
desviación típica de la prueba, (H16) es la desviación
típica del ítem, (J12) es la desviación típica de la
prueba, y (K16) es la correlación punto biserial.

29. Luego se realiza el cálculo completo de la
ecuación, de la cual resulta lo siguiente.

30. Donde, (K16) es la rpb, calculada anteriormente, (J12)
es la desviación típica, (H16) es la desviación típica del
ítem y (X9) es la raíz del calculo inferior de la
ecuación realizado anteriormente.

31. • La Tabla finalmente queda de
la siguiente forma.
• Donde se observan los
cambios que producía el
aporte de varianza dado por
cada ítem en la correlación con
la prueba.

32. Media
• La media se obtiene al sumar los puntajes brutos
de los sujetos y dividirlo entre el número de
personas que contesto la prueba. En Excel, el
calculo se realiza fácilmente, se coloca el signo =
seguido de la palabra PROMEDIO, y se coloca
el sombreado del total, de cada persona en la
prueba, como se muestra a continuación