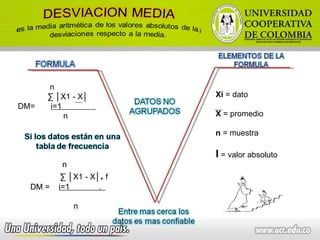
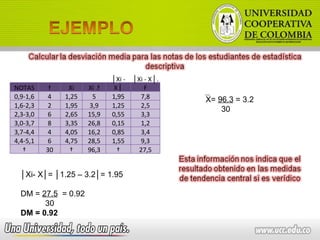
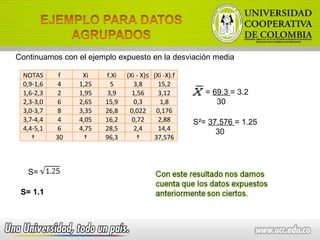
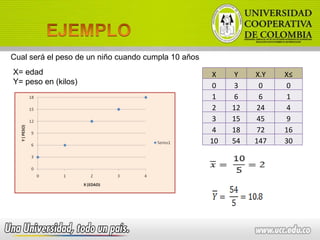
El documento describe las fortalezas y debilidades de una persona, incluyendo responsabilidad, respeto por los demás y dormir demasiado. También describe contenidos académicos como medidas de dispersión y regresiones lineales, así como evidencias requeridas como portafolios e interpretación de datos. Finalmente, presenta una matriz para valorar aspectos como actividades desarrolladas y análisis de rendimiento académico.

4. Mis fortalezas Responsabilidad en cualquier situación. Respetuosa con los demás. Tolerante con mi familia. Reconocer mis errores. Mis debilidades Dormir demasiado. Ver mucha televisión

9. 5. Saberes Esenciales Contenidos: 5.1 Saber Conocer: Medidas de dispersión, varianza, desviación media, coeficiente de variación, desviación estándar, Desigualdades de Chevicheff, regresiones lineales. 5.2 Saber Ser: - Valores: Responsabilidad – lealtad – tolerancia – legalidad de la información - Actitudes: respeto por la información en sus resultados y su interpretación - Normas: Responsabilidad social. 5.3 Saber Hacer: Desarrolló de cuestionarios, Análisis de datos, Graficación en Excel, Vinculación Excel Word, Interpretación de las variables 6. Evidencias Requeridas: 6.1 Producto: Portafolios, Cuestionarios, mapas mentales, mentefactos, problemas con las medidas de tendencia central interpretados 6.2 Desempeño: Uso del Excel en el cálculo de fórmulas, Interpretación de las medidas de Dispersión. 6.3 Conocimiento: Desarrollo de guías, informes, desarrolló de talleres, pruebas cognitivas, desarrollo de parciales, pruebas ECAES

13. 7. Matriz de Aspectos a Valorar: Aspectos a Valorar Excelente Bueno Por Mejorar Las actividades no desarrolladas en el corte anterior aparecen evidenciadas. El autodiagnóstico aparece referenciado en la tabla y su correspondiente mapa mental. El análisis de rendimiento académico se encuentra determinado y analizado de acuerdo a los valores de las medidas de tendencia central y las medidas de dispersión.. Los ejercicios propuestos en la página 117 hasta la pagina 121, del libro “Compendio de estadística descriptiva basado en el desarrollo de competencias básicas”, están desarrollados y justificados. Los ejercicios propuestos están desarrollados y justificados. El Marco teórico del proyecto propuesto responde a los contenidos propuestos en el tema inicial. El análisis de los resultados de las pruebas ECAES, es apropiado. . La asistencia y la participación en todas las actividades de la clase se encuentra evidenciada en los instrumentos de seguimiento de asesoría y listado a clase.

18. n ∑ │ X1 - X│ DM= i=1 . n Xi = dato X = promedio n = muestra l = valor absoluto n ∑ │ X1 - X│ . f DM = i=1 . n

19. n = 20 niños X = 66 = 3.3 = 3 gr/niño 20 │ Xi – X│= │1-3│= │-2│= 2 DM = 28 = 1.4 20 DM = 1.4 Esto nos quiere decir que el promedio que se había calculado para cada niño es el que verdaderamente debería recibir Xi f Xi . F │ Xi - X │ │ Xi - X │ . F 1 4 4 2 8 2 3 6 1 3 3 4 12 0 0 4 4 16 1 4 5 3 15 2 6 6 1 6 3 3 7 1 7 4 4 20 66 28

20. FORMULA n ∑ │ X1 - X│ . f DM = i=1 . n ELEMENTOS DE LA FORMULA Xi = marca de clase X= promedio n = muestra F = frecuencia absoluta

21. X= 96.3 = 3.2 30 │ Xi- X│= │1.25 – 3.2│= 1.95 DM = 27.5 = 0.92 30 DM = 0.92 NOTAS f Xi Xi .f │ Xi - X│ │ Xi - X│. F 0,9-1,6 4 1,25 5 1,95 7,8 1,6-2,3 2 1,95 3,9 1,25 2,5 2,3-3,0 6 2,65 15,9 0,55 3,3 3,0-3,7 8 3,35 26,8 0,15 1,2 3,7-4,4 4 4,05 16,2 0,85 3,4 4,4-5,1 6 4,75 28,5 1,55 9,3 30 96,3 27,5

22. Es la medida de dispersión usada en el calculo de márgenes de error n ∑ (Xi – X)² S²= i=1 . n Si los datos están en una tabla de frecuencia n ∑ (Xi – X)² . f S²= i=1 . n n ∑ (Xi – X)² . f S²= i=1 . n

23. S= n .f S= n S= n .f

24. = 66 = 3.3 20 1-3.3 = -2.3 S²= 58.2 = 2.91 20 S = = 1.7 S= 1.7 Xi f Xi . f (Xi- X) (Xi - X)².f 1 4 4 -2,3 21,16 2 3 6 -1,3 5,07 3 4 12 -0,3 0,36 4 4 16 0,7 1,96 5 3 15 1,7 8,67 6 1 6 2,7 7,29 7 1 7 3,7 13,69 20 58,2

25. Continuamos con el ejemplo expuesto en la desviación media = 69.3 = 3.2 30 S²= 37.576 = 1.25 30 S= S= 1.1 NOTAS f Xi f.Xi (Xi - X)² (Xi -X).f 0,9-1,6 4 1,25 5 3,8 15,2 1,6-2,3 2 1,95 3,9 1,56 3,12 2,3-3,0 6 2,65 15,9 0,3 1,8 3,0-3,7 8 3,35 26,8 0,022 0,176 3,7-4,4 4 4,05 16,2 0,72 2,88 4,4-5,1 6 4,75 28,5 2,4 14,4 30 96,3 37,576

26. Permite medir la variabilidad de los datos en forma porcentual Entre mas alto el % más des confiable será el dato Cv= X100%

27. Continuamos con el ejemplo expuesto en la desviación standart DATOS NO AGRUPADOS DATOS AGRUPADOS Cv= 1.7 x 100% 3.3 Cv= 0.51 = 51% Cv = 1.1 x 100% 3.2 Cv = 0.34 = 34%

28. Puntos dispersos en el plano . . . . . . . . . . . . . . . . . . . . . . . …. . . Formando una recta de regresión lineal

29. Y X Y= mx + b Y = mx + b pendiente intercepto X= variable independiente Y= variable dependiente = = n = cantidad de puntos en el plano X Y X.Y X² X1 Y1 X1 . Y1 X1² X2 Y2 X2 . Y2 X2² X3 Y3 X3 . Y3 X3² Xn Yn Xn . Yn Xn² ∑ X ∑ Y ∑ XY ∑ X²

30. m = covariante varianza

31. Cual será el peso de un niño cuando cumpla 10 años X= edad Y= peso en (kilos) X Y X.Y X² 0 3 0 0 1 6 6 1 2 12 24 4 3 15 45 9 4 18 72 16 10 54 147 30

33. Estandariza los datos en extractos Da valor a cada extracto Se parte del supuesto de que todos los datos están en una distribución normal

34. D I A S E Optimo Mo

35. S²= 37.576 = 1.25 30 S= S= 1.1 NOTAS f Xi f.Xi (Xi - X)² (Xi -X).f 0,9-1,6 4 1,25 5 3,8 15,2 1,6-2,3 2 1,95 3,9 1,56 3,12 2,3-3,0 6 2,65 15,9 0,3 1,8 3,0-3,7 8 3,35 26,8 0,022 0,176 3,7-4,4 4 4,05 16,2 0,72 2,88 4,4-5,1 6 4,75 28,5 2,4 14,4 30 96,3 37,576

36. 2.1 3.2 4.3 I A S E 0.2=20% 0.23=23% 0.3=30% 0.27=27% 3,5 2 1 1,6 2,7 1,2 4,3 1,8 2,7 3,3 3,3 1,3 5 3,3 3,4 3,8 4,8 2,4 4,4 4,4 4,7 2,7 4,5 2,7 3,1 2,5 5 3,4 3,2 4,5 I 6 A 7 S 9 E 8