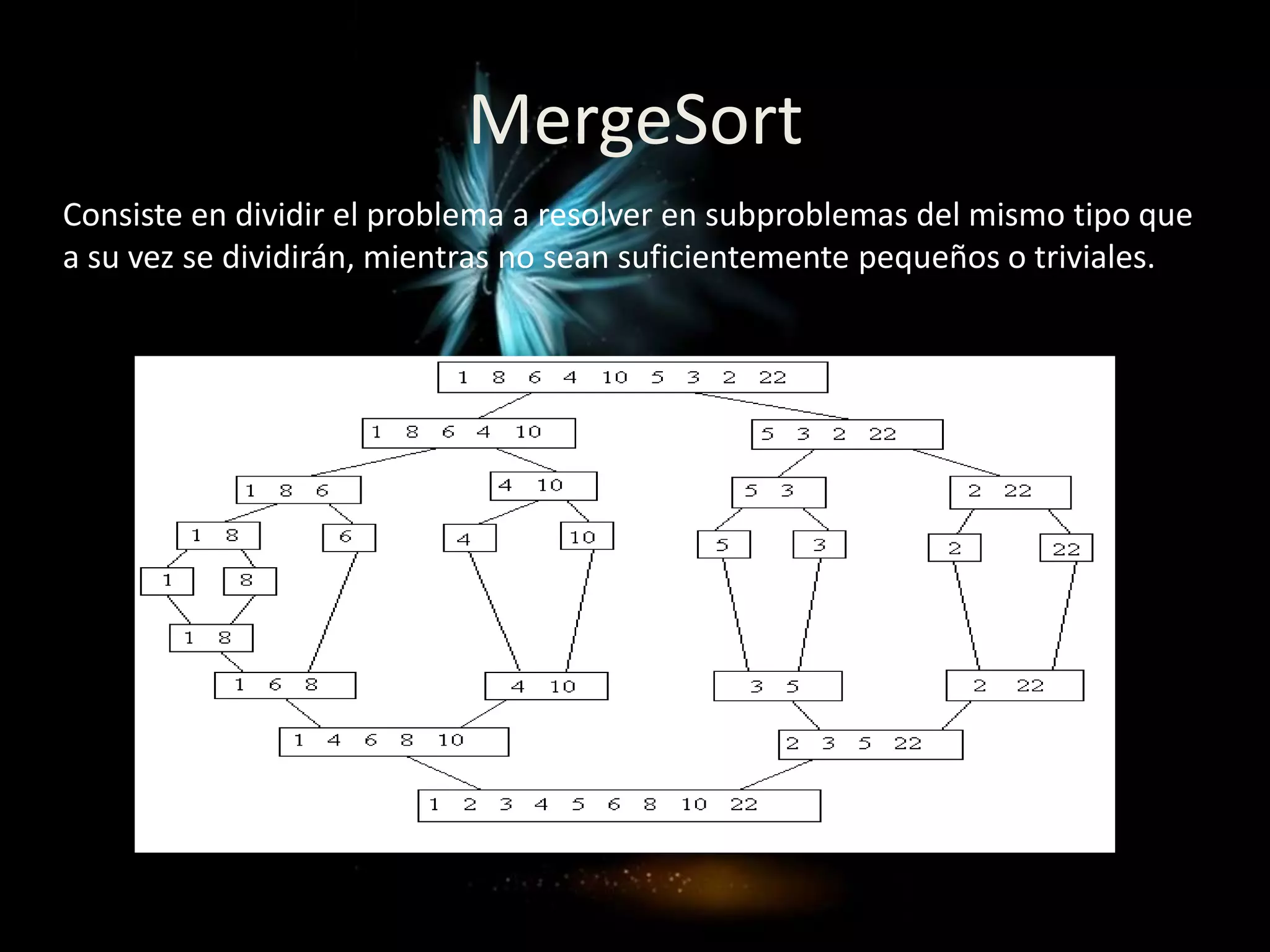
Este documento describe diferentes algoritmos de ordenación como la inserción directa, el método de la burbuja y el mergesort. Explica cómo cada algoritmo ordena una lista de números de forma incremental reubicando los elementos para colocarlos en su posición correcta.

1. Programación Dinámica
Realizado por:
Marcano
Corina
Instituto Universitario
Politécnico
Santiago Mariño
Extensión – Porlamar

2. Shell
imagínese una lista de datos ordenados por,
ejemplo estos enteros:
74, 14, 21, 44, 38, 97, 11, 78, 65, 88, 30
Por medio de Shell haremos unas ordenaciones
basadas en la inserción directa

3. El primer sub-array es el formado por
74,97,30
Ahora, ordenaremos los elementos del sub-
array (74,97,30) pero sólo entre ellos,
utilizando el algoritmo de Inserción directa
30, 14, 21, 44, 38, 74, 11, 78, 65, 88, 97
Fíjate como el 30 pasa a la primera posición y
el 97 a el final, todos dando saltos de 5lugares

4. Formemos ahora otro sub-array con 5 salto... partiendo
del segundo elemento (el 14) y contando 5 (tomamos
también el 11) y ya está, porque se acaba el array.
30, 14, 21, 44, 38, 74, 11, 78, 65, 88, 97
Vamos a ordenarlos entre ellos con Inserción directa... el
11 primero y el 14 después.
30, 11, 21, 44, 38, 74, 14, 78, 65, 88, 97
Ahora a por otro... el 21 y el 78
30, 11, 21, 44, 38, 74, 14, 78, 65, 88, 97
Están en orden entre ellos, así que se quedan como están.
Ahora le toca al sub-array formado por el 44 y el 65
30, 11, 21, 44, 38, 74, 14, 78, 65, 88, 97
Que también están en orden entre ellos. y finalmente el 38
y el 88, que también están en orden.
30, 11, 21, 44, 38, 74, 14, 78, 65, 88, 97

5. Luego
30, 11, 21, 44, 38, 74, 14, 78, 65, 88, 97
Ahora, cada número está mucho más cerca de
su posición definitiva
30, 11, 21, 44, 38, 74, 14, 78, 65, 88, 97
Finalmente, el array queda de ésta manera:
11, 14, 21, 30, 38, 44, 65, 74, 78, 88, 97

6. Método de la burbuja
Vamos a recorrer las posiciones del vector desde i=0 hasta i=3.
i = 0 {7 3 5 1 4}
Recorremos el vector desde j=1 hasta j=4 y comparamos vector [0]=7 con vector [j].
Si vector [j]<vector [0] intercambiamos los valores de posición. Vamos a ver cómo
quedaría el vector inicial una vez que termina cada bucle j.
j = 1 {3 7 5 1 4} Se intercambia 3 con 7 j = 2 {3 7 5 1 4} No se intercambia 3 con 5 j =
3 {1 7 5 3 4} Se intercambia 1 con 3 j = 4 {1 7 5 3 4} No se intercambia 1 con 4
i = 1 {1 7 5 3 4}
Recorremos el vector desde j=2 hasta j=4 y comparamos vector [1]=7 con vector [j].
Supongamos que queremos ordenar los siguientes cinco números: 7,3,5,1,4. Estos
números se almacenarán en un vector de la siguiente manera:

7. • j = 2 {1 5 7 3 4} Se intercambia 5 con 7 j = 3 {1 3 7 5 4} Se
intercambia 3 con 5 j = 4 {1 3 7 5 4} No se intercambia 3 con
4
•
i = 2 {1 3 7 5 4}
• j = 3 {1 3 5 7 4} Se intercambia 5 con 7 j = 4 {1 3 4 7 5} Se
intercambia 4 con 5
•
i = 3 {1 3 4 7 5}
• j = 4 {1 3 4 5 7} Se intercambia 5 con 7 ¡Números
ordenados!
• Ya se ve que no es necesario que el bucle i llegue hasta el
valor 4.

8. MergeSort
Consiste en dividir el problema a resolver en subproblemas del mismo tipo que
a su vez se dividirán, mientras no sean suficientemente pequeños o triviales.

9. Consiste en elegir, de entre un conjunto de n elementos de un negocio,
(cada uno con un valor vi , y un peso pi ), aquellos que puedan ser cargados en la
mochila de un individuo, que decide hacer una visita nocturna al negocio. La
mochila resiste un peso máximo P y se debe tener en cuenta que el visitante
pretende acumular el mayor valor posible, entre todos los objetos que recoge.
Este es un claro ejemplo de la presentación de un problema, en el que hay dificultad para
hallar una solución óptima exacta, principalmente por el tiempo que llevaría recorrer y
combinar todas las posibilidades en forma exhaustiva.
Para 20 elementos  se definen 220=1.048.580 subconjuntos o soluciones
Para 60 elementos  se necesitan 365 siglos para resolver el problema, a 1 millón de
soluciones por segundo
Método de la mochila