PRESENTACION GRUPAL CALCULO VECTORIAL UNIDAD 5.pptx

TECNOLOGICO NACIONAL DE
MEXICO
INSTITUTO TECNOLOGICO DE CERRO AZUL
AGOSTO-DICIEMBRE 2023
INGENIERIA INDUSTRIAL
CALCULO VECTORIAL
ACF-0904 3-2-5
DOCENTE: CIRILO ALBERTO LAGOS QUIROZ.
TEMA 5: INTEGRACIÓN MULTIPLE.
01 DE DICIEMBRE DEL 2023

ALUMNOS
PARTICIPANTES:
• ALVARADO HERNÁNDEZ CELSO VENICIO.
• ALVARADO HERNÁNDEZ JESÚS RICARDO.
• AVENDAÑO DE LA CRUZ ALBERTO.
• BACA CARDENAS GUILLERMO.
• CALDERÓN RIVERA JOSÉ ORLANDO.
• CASTELLANOS FRANCO HANNIA.
• CRUZ ZACARIAS KEVIN OBED.
• DE LA CRUZ RAMÍREZ MARLA HIROMI.
• DEL ANGEL FELIPE LUCERO.
• GOMEZ JIMAREZ VIVIANA CECILIA.
• HERNÁNDEZ BAUTISTA MARLY MAYAM.
• HERNÁNDEZ NICOLAS BLANCA LIZETH.
• LANDA MORALES SANTIAGO ABINADI.
• LÓPEZ REYES WENDY PATRICIA.
• LOYA ONOFRE GLORIA YULISA.
• LUGO DE LA CRUZ EDUARDO.
• MARQUEZ BAUTISTA JOSE ANGEL.
• MARTINEZ VICENCIO LAURA JIMENA.
• MORALES MENDIOLA JESUS EMMANUEL.
• ONOFRE DOMÍNGUEZ AYLIN GUADALUPE.
• PICHARDO REYES SULEMI YURITZY.
• SOBREVILLA CRUZ SALMA PATRICIA.
Cerro Azul, Ver., a 01 de Diciembre del 2023.

TEMARIO
5.1 Cálculo de áreas e integrales dobles.
5.2 Integrales iteradas.
5.3 Integral doble en coordenadas rectangulares.
5.4 Integral doble en coordenadas polares.
5.5 Integral triple en coordenadas rectangulares. Volumen.
5.6 Integral triple en coordenadas cilíndricas y esféricas.
5.7 Campos vectoriales.
5.8 La Integral de línea.
5.9 Divergencia, rotacional, interpretación geométrica y física.
5.10 Teoremas de integrales.

5.1 CÁLCULO DE ÁREAS E INTEGRALES DOBLES.
Las integrales dobles son una manera de integrar sobre una región bidimensional. Entre otras cosas
nos permite calcular el volumen bajo una superficie.
Dada una función de dos variables, f (x,y) f(x,y), puedes encontrar el volumen bajo una superficie,
entre la gráfica y una región rectangular del plano "X“ y "xy" al tomar la integral de una integral.
Esta es una función de y:
¹
²
(∫ f(x,y)dy
∫½
ʸ ¹ ˣ
ˣ
Llamamos a esta "integral doble“
puedes cambiar el orden de integración para calcular el mismo volumen.
Esta es una función de X:
∫¹(∫ f(x,y)dx
ˣ
ˣ²
¹
ʸ
²
ʸ
Las cuentas se verán y serán muy diferentes, pero el resultado es el mismo.

EJEMPLO 1.-
Calcular el área usando doble integral.
Región limitada por las curvas.
Calculamos los puntos de intersección.
x²= 3x x=0
x²-3x=0 x=3 Tipo 1
X(x-3)=0 0<x<3
x²<y<3x
A= ∫ ∫ dydx
ˣ
ˣ²
Y=3x
Y=x²
³ ³
⁰
³ˣ ³
= ∫ y| dx= ∫ (3x-x)dx= (
3𝑥2
2
-
𝑥3
3
) | = (
3(3)2
2
-
(3)3
3
)-(
3(0)2
2
-
(0)3
3
)
³
⁰ ²
ˣ ⁰
=
27
2
−
27
3
− 0 =
9
2

EJEMPLO 2.-
Región limitada por las curvas 𝑥 = 𝑦2
𝑥 = 2
2 = 𝑦2
± 2 = 𝑦
Tipo 2
− 2 < 𝑦 < 2
𝑦2 < x < 2
A= 𝑑𝐴
A= −√2
√2
𝑦2
2
𝑑𝑥𝑑𝑦 = −√2
√2
𝑥 I 2
𝑦2
𝑑𝑦 = −√2
√2
2 − 𝑦2
𝑑𝑦
= 2𝑦 −
𝑦3
3
I √2
−√2
= (2 2 −
( 2)3
3
)− 2 − 2 −
− 2
3
3
= 2 2 −
2 2
3
− − 2 −
−2 2
3
=
=2 2 −
2
3
2 + 2 2 −
2
3
2 =
8
3
√2

EJEMPLO 3.-
Resuelve la siguiente integral doble.
0
1
√𝑥
1+𝑥
2𝑥𝑦𝑑𝑦 }𝑑𝑥
= 0
1
{ √𝑥
1+𝑥
2𝑥𝑦 𝑑𝑦 }𝑑𝑥
= 0
1
{2𝑥
𝑦2
2
]
1 + 𝑥
√𝑥
}dx
= 0
1
{𝑥𝑦2|
1 + 𝑥
√𝑥
}𝑑𝑥 = 0
1
{𝑥 (1 + 𝑥)2−𝑥 𝑥 2}𝑑𝑥
= 0
1
𝑥 1 + 2𝑥 + 𝑥2
− 𝑥 ∗ 𝑥 𝑑𝑥 = 0
1
𝑥 + 22
+ 𝑥3
− 𝑥2
𝑑𝑥
= 0
1
(𝑥 + 𝑥2 + 𝑥3) 𝑑𝑥 =
𝑥2
2
+
𝑥3
3
+
𝑥4
4
|
1
0
=
1
2
+
1
3
+
1
4
− 0 =
13
12

5.2 INTEGRALES ITERADAS.
Una integral iterada es una integral evaluada varias veces sobre la misma variable (en contraste
con una integral múltiple, que consiste en un número de integrales evaluadas con respecto a
diferentes variables).
Es importante tener en cuenta en qué posición se dan los límites de las integrales en cuestión para
saber en qué orden se ejecutarán los procesos de integración simple, es decir reconocer si se va a
integrar primero considerando el diferencial dx o el dy o viceversa.
Área de una región en el plano del eje "x“
Si la región R está definida por 𝑎 ≤ 𝑥 ≤ 𝑏 y g1(x)≤ 𝑦 ≤ g2 (x), donde g1(x) y g2 (x) son funciones
continuas en el eje x del intervalo [a,b]. La Región Restá dada por:
A= 𝑎
𝑏
𝑔2(𝑥)
𝑔1(𝑥)
𝑑𝑦𝑑𝑥
Área de una región en el plano del eje “y”
Si la región r está definida por ∁≤ 𝑦 ≤ 𝑑 y h1 (x)≤ 𝑥 ≤ h2 (y) donde h1 (y) y h2 (y) son funciones
continuas en el eje x del intervalo [c,d]. La Región R está dada por:
𝐴 =
𝑐
𝑑
ℎ1
ℎ2
(𝑦)
(𝑦)
𝑑𝑥𝑑𝑦

EJEMPLO 1.-
Calcular la integral iterada = 1
3
0
2
(𝑥𝑦 + 𝑥2
𝑦3
𝑑𝑦 𝑑𝑥
= 0
2
(𝑥𝑦 + 𝑥2 𝑦3)𝑑𝑦 =
𝑥𝑦2
2
+ 𝑥2 𝑦4
4
]
2
0
=
𝑥
2
2 2 − 0 2 +
𝑥2
4
2 4 − 0 4 =
𝑥
2
4 − 0 +
𝑥2
4
16 − 0
=
𝑥
2
4 +
𝑥2
4
10 = 2𝑥 + 4𝑥2
= 1
3
(2𝑥 + 4𝑥2)𝑑𝑥 = 2
𝑥2
2
+ 4
𝑥3
3
]
3
1
= 𝑥2 +
4
3
𝑥3]
3
1
=[(3)2
−(1)2
]+
4
3
3 3
− 1 3
= 9 − 1 +
4
3
27 − 1 = 8 +
4
3
26 = 8 +
104
3
=
24+104
3
=
128
3

EJEMPLO 2.-
= 1
3
1
2
6𝑥𝑦2
−
4𝑥
𝑦
𝑑𝑦𝑑𝑥
= 1
2
(6𝑥𝑦2 −
4𝑥
𝑦
𝑑𝑦 = 6𝑥
𝑦3
3
− 4𝑥𝐿𝑛𝑙𝑦]
2
1
= 2𝑥𝑦3 − 4𝑥 𝐿𝑛𝑙𝑦|]
2
1
=2𝑥 2 3 − 1 3 − 4𝑥 𝐿𝑛2 − 𝐿𝑛1 = 2𝑥 8 − 1 − 4𝑥 𝐿𝑛2 = 14𝑥 − 4𝑥 𝐿𝑛2
= 1
3
14𝑥 − 4𝑥 𝐿𝑛2 𝑑𝑥 = 14
𝑥2
2
− 4 𝐿𝑛
2𝑥2
2
]
3
−1
= 7𝑥2
− 2𝐿𝑛 2𝑥2
]
3
1
=7 3 2
− −1 2
− 2𝐿𝑛2 3 3
− −1 2
= 7 9 − 1 − 2 𝐿𝑛 2 9 − 1
=56 − 16 𝐿𝑛2 = 44.91

EJEMPLO 3.-
. −1
2
2𝑥2−2
𝑥2+𝑥
𝑥𝑑𝑦 𝑑𝑥
= 2𝑥2−2
𝑥2+𝑥
𝑥𝑑𝑦 = 𝑥𝑦] 𝑥2 + 𝑥
2𝑥2
− 2
= 𝑥 [𝑥2 + 𝑥 − (2𝑥2 − 2)]
=𝑥 𝑥2
− 𝑥 − 2𝑥2
+ 2 = 𝑥3
+ 𝑥2
− 2𝑥3
+ 2𝑥 = −𝑥3
+ 𝑥2
+ 2𝑥
1
2
−𝑥3
+ 𝑥2
+ 2𝑥 𝑑𝑥 =
−𝑥4
4
+
𝑥3
3
+ 2
𝑥2
2
]
2
−1
=−
1
4
𝑥4
+
1
3
𝑥3
+ 𝑥2
]
2
−1
= −
1
4
[24
− −1 4
] +
1
3
[ 2 3
− −1 3
] + [22
− (−1)2
]
=-
1
4
16 − 1 +
1
3
8 − −1 + 4 − 1
=−
1
4
∗ 15 +
1
3
9 + 3 = −
15
4
+ 3 + 3 = −
15
4
+ 6
=-
15+24
4
=
9
4

5.3 INTEGRAL DOBLE EN COORDENADAS
RECTANGULARES.
En coordenadas rectangulares, una integral doble representa la integral de una función definida
sobre una región bidimensional en el plano.
La forma general de una integral doble en Coordenadas rectangulares es la siguiente:
𝑓 𝑥, 𝑦 𝑑𝐴
Donde f (x,y) es la función que desea integrar y dA representa el elemento diferencial de área
sobre la región de integración. La región de integración se define especificando los límites de
integración para “x“ y "y", que determinan el tamaño y la forma de la región.
La evaluación de una integral doble en coordenadas rectangulares implica la aplicación de las
reglas de integración adecuadas. Estas reglas pueden involucrar cambios de variable,
descomposición en regiones más simples.
La integral resultante dará como resultado un número que representa el valor de la integral sobre
la región de integración específica.

EJEMPLO 1.-
• 0
1
1
2 𝑥𝑒𝑥
𝑦
𝑑𝑦𝑑𝑥 0
1
𝑋𝑒𝑥
𝐿𝑛|2|𝑑𝑥
=𝑥 𝑒𝑥
1
2 1
𝑦
𝑑𝑦 𝐿𝑛|2| 0
1
𝑥𝑒𝑥
𝑑𝑥
=𝑥 𝑒𝑥
𝐿𝑛 𝐿𝑦𝑙 |
2
1
𝑥 𝑒𝑥
=𝑥 𝑒𝑥
𝐿𝑛 2 − 𝐿𝑛 1 1 𝑒𝑥
=𝑥 𝑒𝑥 𝐿𝑛 |2| 0 𝑒𝑥
𝐿𝑛|2|[𝑥𝑒𝑥
− 𝑒𝑥
|
1
0
]
𝐿𝑛 2 1𝑒1 − 𝑒1 − (0𝑒0 − 𝑒0)
𝐿𝑛 2 0 − 0 − 1 = 𝐿𝑛|2|

EJEMPLO 2.-
• 0
1
1
2
4𝑥3 − 92𝑦2 𝑑𝑦𝑑𝑥
= 1
2
4𝑥3𝑑𝑦 − 9 1
2
𝑥2𝑦2𝑑𝑦
=4𝑥3
1
2
𝑑𝑦 − 9𝑥2
1
2
𝑦2
𝑑𝑦
=4𝑥3𝑦|
2
1
− 9𝑥2 𝑦3
3
|
2
1
=4𝑥3
2 − 1 − 3𝑥2
(23
− 13
)
= 0
1
4𝑥3
− 21𝑥2
𝑑𝑥
=4
𝑥4
4
|
1
0
− 21
𝑥3
3
|
1
0
=1 − 7 = −6
• 1
4
1
2 𝑥
𝑦
+
𝑦
𝑥
𝑑𝑦𝑑𝑥
= 1
2 𝑥
𝑦
𝑑𝑦 + 1
2 𝑦
𝑥
𝑑𝑦
=𝑥 1
2 1
𝑦
dy +
1
𝑥 1
2
𝑦𝑑𝑦
=𝑥𝐿𝑛 𝑦
2
1
+
1
𝑥
𝑦2
2
|
2
1
=𝑥 𝐿𝑛 2 − 𝐿𝑛 1 +
1
2𝑥
(22
− 12
)
=𝑥 𝐿𝑛 2 +
1
2𝑥
∗ 3
=𝐿𝑛 |2| 1
4
𝑥𝑑𝑥 +
3
2 1
4 1
𝑥
𝑑𝑥
=𝐿𝑛 2
𝑥2
2
4
1
+
3
2
𝐿𝑛|𝑥|
4
1
=
1
2
𝐿𝑛 2 42
− 12
+
3
2
(𝐿𝑛 4 − 𝐿𝑛|1|)
=
15
2
𝐿𝑛 2 +
3
2
𝐿𝑛|4|
EJEMPLO 3.-

5.4 INTEGRAL DOBLE EN COORDENADAS POLARES.
Para cambiar una integral doble de coordenadas rectangulares a coordenadas polares se hace una
transformación.
Iniciando desde el centro de la doble integral hacia afuera, los límites inferior y superior de la
primera integral representan el radio de la circunferencia y después los límites de la segunda
integral representan el área bajo la curva, y finalmente, la conversión es la siguiente:
𝑐
𝑑
𝑎
𝑏
𝑓 𝑥, 𝑦 𝑑𝑦𝑑𝑥 =
𝜃1
𝜃2
𝑟2
𝑟1
𝑓(𝑟 sin 𝜃, 𝑟 cos 𝜃)𝑟𝑑𝑟𝑑𝜃
La integral doble en coordenadas polares involucra realizar una integral doble en la región descrita
por las coordenadas polares.
𝑓 𝑟, 𝜃 𝑟 𝑑𝑟 𝑑𝜃
Donde f(r,𝜃) es la función a integrar, r es la distancia desde el origen al punto en coordenadas
polares y 𝜃 es el ángulo desde el eje x positivo al punto en coordenadas polares.

EJEMPLO 1.-
• 0
𝜋
1
2
3𝑥 + 4𝑦2
𝑑𝐴
= 0
𝜋
1
2
(𝑟𝑐𝑜𝑠𝜃 + 4𝑟2
𝑠𝑒𝑛2
𝜃) 𝑟 𝑑𝑟 𝑑𝜃
= 0
𝜋
1
2
3𝑟2
𝑐𝑜𝑠𝜃 + 4𝑟3
𝑠𝑒𝑛2
𝜃 𝑟𝑑𝑟𝑑𝜃 = 0
𝜋
[3𝑐𝑜𝑠𝜃 1
2
𝑟2
𝑑𝑟 + 4 𝑠𝑒𝑛2
𝜃 1
2
𝑟2
𝑑𝑟𝑑𝜃
= 0
𝜋
[3𝑐𝑜𝑠𝜃
𝑟3
3
+ 4 𝑠𝑒𝑛2𝜃(
𝑟4
4
]|
2
1
𝑑𝜃
= 0
𝜋
[𝑐𝑜𝑠𝜃 23 − 13 + 𝑠𝑒𝑛2𝜃(24 − 14] 𝑑𝜃 = 0
𝜋
(7 cos 𝜃 + 15 𝑠𝑒𝑛𝜃)𝑑𝜃
=7 0
𝜋
𝑐𝑜𝑠𝜃𝑑𝜃 + 15 0
𝜋
𝑠𝑒𝑛2
𝜃𝑑𝜃 = 7𝑠𝑒𝑛𝜃 + 15(
1
2
−
1
2
𝑐𝑜𝑠2𝜃)
=7𝑠𝑒𝑛𝜃 +
15
2
𝜃 −
15
2
cos 2𝜃|
𝜋
0
=7𝑠𝑒𝑛𝜋 +
15
2
𝜋 −
15
2
𝑐𝑜𝑠2𝜋 − 7𝑠𝑒𝑛0 −
15
2
0 +
15
2
𝑐𝑜𝑠2(0)
=
15
2
𝜋 −
15
2
+
15
2
=
15
2
𝜋
𝑥 = 𝑟𝑐𝑜𝑠𝜃
𝑦 = 𝑟𝑠𝑒𝑛𝜃
𝑟2
= 𝑥2
+ 𝑦2
𝑡𝑎𝑛𝜃 =
𝑦
𝑥

EJEMPLO 2.-
• 𝜋
4
𝜋
2
0
√8 1
5+𝑥2+𝑦2 𝑑𝐴
= 𝜋
4
𝜋
2
0
√8 1
5+𝑟2 𝑟𝑑𝑟𝜃
= 𝜋
4
𝜋
2
0
√8 1
𝑢
𝑑𝑢
𝑑𝑥
𝑑𝜃 𝜋
4
𝜋
2
[
1
2 0
√8 𝑑𝑢
𝑢
] 𝑑𝜃 = 𝜋
4
𝜋
2 1
2
𝐿𝑛 5 + 𝑟2 𝜃
0
𝑑𝜃
= 𝜋
4
𝜋
2 1
2
𝐿𝑛 5 + 8 −
1
2
𝐿𝑛 5 + 0 𝑑𝜃 = 𝜋
4
𝜋
2 1
2
( 𝐿𝑛13 − 𝐿𝑛5)𝑑𝜃
=
1
2
𝐿𝑛 13 − 𝐿𝑛5 𝜋
4
𝜋
2
𝑑𝜃 =
1
2
(𝐿𝑛13 − 𝐿𝑛5)(𝜃)
𝜋
2
𝜋
4
=
1
2
𝐿𝑛13 − 𝐿𝑛5
𝜋
2
−
𝜋
4
=
𝜋
8
(𝐿𝑛
13
5
)
𝑟2
= 𝑥2
+ 𝑦2
𝑢 = 5 + 𝑟2
𝑑𝑢 = 2𝑟𝑑𝑟
𝑑𝑢
2𝑥
= 𝑑𝑟
EJEMPLO 3.-
• 𝑥2 + 𝑦2
𝑑𝑥𝑑𝑦
V= 0
2
0
2𝜋
𝑟 𝑟𝑑𝜃𝑑𝑟
V= 0
2
𝑟2𝑑𝑟 0
2𝜋
𝑑𝜃 = 𝑣 = 0
2
𝑟2𝑑𝑟𝜃|
2𝜋
0
=2𝜋 0
2
𝑟2
𝑑𝑟 = 2𝜋
𝑟3
3
|
2
0
=
16
3
𝜋
𝑥2
+ 𝑦2
= 4
0 ≤ 𝑦 ≤ 2
0 ≤ 𝜃 ≤ 2𝜋
𝑟 = 𝑥2 + 𝑦2

5.5 INTEGRAL TRIPLE EN COORDENADAS
RECTANGULARES . VOLUMEN.
Si F(x,y,z) es una función definida en una región cerrada D y acotada en el espacio, como la región
ocupada por una bola sólida o un montón de arcilla, entonces, la integral de F sobre D se define de
la siguiente manera.
Partimos una región en forma de caja rectangular que contiene a D en celdas rectangulares
mediante planos paralelos a los ejes coordenados.
Numeraremos las celdas que están dentro de D desde 1 hasta 𝑛 en algún orden, donde la K-ésima
celda tiene las dimensiones ∆x_k por ∆y_k por ∆z_k y volumen ∆v_k= ∆ x_k∆y_k ∆z_k.
Seleccionando un punto (x_k,y_k,z_k) en cada celda y formamos la suma…
Sn□=∑_(k=1)´n ≠ 𝐹□ (x_k,y_k,z_k) ∆v_k.
Volumen
Si F es una función constante cuyo valor es 1, entonces las sumas de la ecuación (1) se reduce a:
Sn=∑≅ □𝐹(𝑥_k,y_k,z_k)∆v_(k=)∑ ≅ □𝐿∆_(k=)□□∑≅ □∆𝑣_(𝑘1)□
Cuando ∆x_k, ∆y_k, ∆z_k tienden a cero, las celdas ∆v_(k1) se hacen cada vez más pequeñas y más
numerosas, y cubren una parte cada vez mayor de D. Por lo tanto, definimos el volumen de D como
la integral triple.

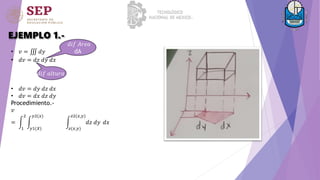
EJEMPLO 1.-
• 𝑣 = 𝑑𝑦
• 𝑑𝑣 = 𝑑𝑧 𝑑𝑦 𝑑𝑥
• 𝑑𝑣 = 𝑑𝑦 𝑑𝑧 𝑑𝑥
• 𝑑𝑣 = 𝑑𝑥 𝑑𝑧 𝑑𝑦
Procedimiento.-
𝑣
=
1
2
𝑦1(𝑋)
𝑦2(𝑥)
𝑧(𝑥,𝑦)
𝑧2(𝑥,𝑦)
𝑑𝑧 𝑑𝑦 𝑑𝑥
𝑑𝑖𝑓 𝐴𝑟𝑒𝑎
dA
𝑑𝑖𝑓 𝑎𝑙𝑡𝑢𝑟𝑎

Hallar el volumen del sólido limitado en el primer octante por los planos coordenados y por el plano
3𝑥 + 2𝑦 + 𝑧 = 6
• 𝑣 = 0
2
0
6−3𝑥
2
6−3𝑥−2𝑦
𝑑𝑧𝑑𝑦𝑑𝑧
= 0
2
0
6−3𝑥
2 6 − 3𝑥 − 2𝑦 𝑑𝑦𝑑𝑥
= 6 − 3𝑥
6−3𝑥
2
− 0 − [(
6−3𝑥
2
) 2 − 02]
=
1
2
(6 − 3𝑥)2
−
1
4
(6 − 3𝑥)2
=
1
4 0
2
(6 − 3𝑥)2𝑑𝑥 =
1
4
(−
1
4
) 6 − 3𝑥 3|
2
0
= −
1
36
6 − 3 2 3 − 6 − 3 0 3 = −
1
36
− −
2
6
= 6𝑢3
EJERCICIO 1.-
(2|
6 − 3𝑥 − 2𝑦
0
= 6 − 3𝑥 − 2𝑦 𝑣 = 6 − 3𝑥
𝑑𝑣 = 3𝑑𝑥
𝑑𝑥 = 𝑑𝑣/−3
}
𝑢2( 𝑑𝑢
−3)
−
1
3
𝑢3
3
→ −
1
9
𝑢3

EJEMPLO 2.-
Hallar el volumen del solido limitado en el primer octante por los planos coordenados y las
superficies.
Sup =𝑧 = 9 − 𝑥2
𝑦 = 9 − 𝑥2
9 − 𝑥2
• 𝑣 = 0
3
0
9−𝑥2
0
9−𝑥2
𝑑𝑧 𝑑𝑦 𝑑𝑧
• 𝑣 = 0
3
0
9−𝑥2
0
9−𝑥2
𝑑𝑧𝑑𝑦𝑑𝑥 → 0
9−𝑥2
𝑑𝑧 = (𝑧|9 − 𝑥2
0
= 9 − 𝑥2
= 0
3
0
9−𝑥2
9 − 𝑥2
𝑑𝑦𝑑𝑥 (9 − 𝑥2
0
9−𝑥2
𝑑𝑦 = 9 − 𝑥2
∗ (𝑦)|9 − 𝑥2
0
= (9 − 𝑥2
)2
= 0
3
9 − 𝑥2
𝑑𝑥 = 0
3
81 − 18𝑥2
+ 𝑥4
𝑑𝑥
=81𝑥 − 6𝑥3 +
1
5
𝑥5|
3
0
= 81 3 − 0 − 6 33 − 0 +
1
5
[35 − 0]
=
648
5
≅ 129.6𝑢3

EJEMPLO 3.-
• 𝑏𝑦 𝑥 = 0, 𝑥 = 1, 𝑦 = 0, 𝑦 = 1, 𝑧 = 0, 𝑎𝑛𝑑 𝑧 = 𝑥𝑦
V= 0
|𝑑𝑣
V= 0
𝑥𝑦
|𝑑𝑧𝑑𝑦𝑑𝑥
V= 0
1
0
1
𝑑𝑦 𝑑𝑥 = 0
1
0
1
𝑥𝑦𝑑𝑦𝑑𝑥
= 0
1 1
2
𝑥𝑦2 1
0
𝑑𝑥 = 0
1 1
2
𝑥 1 2 − 0 2 dx
= 0
1 1
2
𝑥𝑑𝑥 =
1
4
𝑥2 1
0
=
1
4
[ 1 2
− (0)2
]
=
1
4
𝑐𝑢𝑏𝑖𝑐 𝑢𝑛𝑖𝑡 = 0.25 𝑐𝑢𝑏𝑖𝑐 𝑢𝑛𝑖𝑡𝑠

5.6 INTEGRALES TRIPLES EN COORDENADAS
CILÍNDRICAS Y ESFÉRICAS.
Coordenadas cilíndricas.
En el espacio bidimensional 𝑅2, en un punto con coordenadas rectangulares (x,y) se puede
identificar con (𝑟, 𝜃) en coordenadas polares y viceversa, donde 𝑥 = 𝑟 𝑐𝑜𝑠𝜃. 𝑦 = 𝑟 𝑠𝑒𝑛𝜃, 𝑟2
= 𝑥2
+
𝑦2
𝑦 tan 𝜃.
𝑥
𝑦
son las relaciones entre variables.
Entre el espacio tridimensional 𝑅3
, un punto con coordenadas rectangulares (x,y,z) y viceversa.
Podemos utilizar estas mismas relaciones de conversión, añadiendo z como la distancia vertical al
punto desde el plano xy.
Coordenadas esféricas.
Sistemas de coordenadas esféricas, especificamos un punto P por su distancia P desde su origen, el
ángulo polar 𝜃 del eje positivo de la x igual que en el sistema de coordenadas cilíndricas, y el
ángulo P deleje positivo de la z y la línea op.

EJEMPLO 1.-
Evaluar una integral triple sobre una caja cilíndrica.
= 𝑧𝑟 𝑠𝑒𝑛 𝜃 𝑟𝑑𝑟 𝑑𝜃𝑑𝑧 donde la caja cilíndrica B es
𝐵 = 𝑟, 𝜃, 𝑧 10 ≤ 𝑟 ≥ 2,0 ≤ 𝜃 ≤
𝜋
2,0
≤ 𝑧 ≥ 4
Solución
• 𝑧𝑟 𝑠𝑒𝑛𝜃 𝑟 𝑑𝑟 𝑑𝜃𝑑𝑧 = 𝜃=0
𝜃=𝜋
2
𝑟=0
𝑟=2
𝑧=0
𝑧=4
𝑧𝑟 𝑠𝑒𝑛𝜃 𝑟 𝑑𝑧𝑑𝑟𝑑𝜃
• 𝜃=0
𝜃=𝜋
2
𝑟=0
𝑟=2
𝑧=0
𝑧=4
𝑍𝑟 𝑠𝑒𝑛𝜃 𝑟𝑑𝑧𝑑𝑟𝑑𝜃
= ( 0
𝜃=𝜋
2
𝑠𝑒𝑛𝜃𝑑𝜃) 0
2
𝑟2
𝑑𝑟)( 0
4
𝑧𝑑𝑧) = −𝑐𝑜𝑠𝜃
𝜋
2
0
𝑟3
3
2
0
(
22
2
|
4
0
=
64
3

EJEMPLO 2.-
Establecer una integral triple en coordenadas cilíndricas sobre una región general.
Considere la región E dentro del cilindro circular recto con ecuación 𝑟=2𝑠𝑒𝑛 𝜃 delimitada abajo por
el plano 𝑟𝜃 y delimitada por la esfera de radio 4 centrada en el origen.
Establece la función f(𝑟,𝜃𝑧)
Solución
E= 𝑟, 𝜃, 𝑧 0 ≤ 𝜃 ≤ 𝜋, 0 ≤ 𝑟 ≤ 2 𝑠𝑒𝑛𝜃, 0 ≤ 𝑧 ≤ 16 − 𝑟2}
Integral triple
• 𝑓 𝑟, 𝜃, 𝑧 𝑟𝑑𝑧𝑑𝑟𝑑𝜃 = 𝜃=0
𝜃=𝜋
𝑟=0
𝑟=2𝑠𝑒𝑛𝜃
𝑧=0
𝑧= 16−𝑟2
𝑓 𝑟, 𝜃, 𝑧 𝑟𝑑𝑧𝑑𝑟𝑑𝜃

EJEMPLO 3.-
• Evaluar una integral triple en coordenadas esféricas.
Evalué la integral = 𝜃=0
𝜃=2𝜋
𝑝.0
𝜋
2
𝑝=0
𝑝=1
𝑝2𝑠𝑒𝑛 𝑃𝑑𝑝𝑑𝑝𝑑𝜃
iterada
Solución
= 0
2𝜋
0
𝜋
2
0
1
𝑝2
𝑠𝑒𝑛 𝑝𝑑𝑝𝑑 𝑝𝑑𝜃 = 0
2𝜋
𝑑𝜃 0
𝜋
2
𝑠𝑒𝑛 𝑝𝑑𝑝 0
1
𝑝2
𝑑𝑝 =
=(2𝜋)1 (
1
3
) =
2𝜋
3

5.7 CAMPO VECTORIAL.
Los campos vectoriales son una herramienta importante para describir muchos conceptos físicos,
como la gravitación y el electromagnetismo, que afectan al comportamiento de los objetos en una
gran región de un plano o del espacio.
También son útiles para tratar el comportamiento a gran escala como las tormentas atmosféricas o
las corrientes oceánicas de aguas profundas.
En esta sección examinando las definiciones básicas y los gráficos de los campos vectoriales para
poder estudiarlos con más detalle en el resto de este capítulo.
Un campo vectorial F en 𝑅2
es una de un vector bidimensional F(x,y) a cada punto (x,y) de un
subconjunto D es el dominio del campo vectorial.
Un campo vectorial F en 𝑅3 es una asignación de un vector tridimensional F(x,y,z) de un
subconjunto D de 𝑅3. El subconjunto D es el campo vectorial.

EJEMPLO 1.-
• 𝐹→
𝑥, 𝑦, 𝑧 = 𝑥𝑦2
𝑧3
𝑗 + 𝑥3
𝑦𝑧2
𝑗 + 𝑥2
𝑦3
𝑧𝑘
• 𝐹→ 𝑥, 𝑦, 𝑧 = 𝑁 = 𝑥, 𝑦, 𝑧 𝑖 + 𝑀 𝑥, 𝑦, 𝑧 𝑗 + 𝑃 𝑥, 𝑦, 𝑧 𝑘
div.𝑓→𝑣→𝐹→ =
𝜕𝑁
𝜕𝑋
+
𝜕𝑀
𝜕𝑦
+
𝜕𝑝
𝜕𝑧
•
𝜕𝑁
𝜕𝑍
=
𝜕
𝜕𝑋
𝑥𝑦2
𝑧3
= 𝑦2
𝑧3
𝑖 ;
𝜕𝑀
𝜕𝑦
𝑥3
𝑦𝑧2
= 𝑥3
𝑧2
𝑗𝑖
•
𝜕𝑝
𝜕𝑧
=
𝜕
𝑎𝑧
𝑥2𝑦3𝑧 = 𝑥2𝑦3
• ∇→. 𝐹→ = 𝑦2𝑧3 + 𝑥3𝑧2 + 𝑥2𝑦3
EJEMPLO 2.-
• Hallar un vector asociado a un punto dado.
Supongamos que F (x,y) = ( 2𝑦2
+ 𝑥 − 4 𝑖 + cos 𝑥 𝑗 es un campo vectorial en 𝑅2
¿Qué vector está asociado el punto (0,-1)?
𝐹 0,1 = 2 −1 2 + 0 − 4 𝑖 + cos 0 𝑗 = −2𝑖 + 𝑗

EJEMPLO 1.-
• 𝐹 𝑥, 𝑦 𝑑𝑠
• Datos del problema
X=𝑥 𝑡 . 𝑦 = 𝑡 , 𝑧 = 𝑧 𝑡 𝑟→ 𝑡 = 𝑥 𝑡 𝑖 + 𝑦 𝑡 𝑗 + 𝑧 𝑡 𝑘 𝑎 < 𝑡 > 𝑏
𝑟→(𝑡) = 𝑡, 𝑡2𝑓3) 𝑡 = ∈ [−1,1], 𝑓 = (𝑥, 𝑦, 𝑧) = 𝑓(𝑥𝑦, 𝑦𝑧, 𝑥𝑧)
Solución
• 𝑟→´ 𝑡 = 1,2𝑡, 3𝑡2
• 𝑓 𝑥 𝑡 , 𝑦 𝑡 , 2 𝑡 = 𝑡∗
, 𝑡2
, 𝑡2
∗ 𝑡3
, 𝑡 ∗ 𝑡3
= 𝑡3
, 𝑡5
, 𝑡4
• −1
1
𝑡3, 𝑡5, 𝑡4 . 1,2𝑡, 3𝑡2 𝑑𝑓 = −1
1
𝑡3 + 2𝑡6 + 3𝑡6 𝑑𝑡 = −1
1
𝑡3 + 5𝑡6 𝑑𝑝
• =[
𝑡4
4
+
5𝑡7
7
]=
10
7
F 𝑥, 𝑦 = 𝑥, 𝑦
𝐹(𝑥, 𝑦, 𝑧)=(𝑥2
,𝑦2
, 𝑧2
)

5.8 LA INTEGRAL DE LA LÍNEA.
Una integral de línea acumula elementos a lo largo de una curva. El concepto de integral se puede
extender a dominios de integración más generales, tales como las líneas curvas y las superficies.
Estas integrales se conocen como integrales de línea o integrales de superficie respectivamente.
Una integral de línea es una integral donde la función a integrar es evaluada a lo largo de una
curva. La función integrar puede ser un campo escalar o un campo vectorial, el valor de la integral
curvilínea es la suma de los valores del campo en los puntos de la línea, ponderados por una
función escalar de la curva (habitualmente la longitud del arco o, en el caso de un campo vectorial,
el producto escalar del campo vectorial por un vector diferencial de la curva.
Muchas fórmulas sencillas de la física tienen de forma natural análogas continuas en los términos
de integrales de línea; por ejemplo, el hecho de que el trabajo sea igual a la fuerza multiplicada
por la distancia se puede expresar (en términos de cantidades vectoriales) como:
W=𝐹→ ∗ 𝑑→
Que tiene su paralelismo en la integral de línea:
W= 𝐹→ ∗ 𝑑→
Que acumula los componentes vectoriales a lo largo de un camino continuo, y así calcula el trabajo
realizado por un objeto al moverse a través de un campo.

EJEMPLO 1.-
Integral de línea de un campo escalar
Se desea evaluar la integral de línea:
𝑐
𝑥2 + 𝑦2 + 𝑧2 𝑑𝑠
Sobre la élice 𝑟: 0,2𝜋 → 𝑅3
,
𝑡 → (𝑐𝑜𝑠𝑡, 𝑠𝑒𝑛𝑡, 𝑡)
En primer lugar notemos que: 𝑟´ 𝑡 = −𝑠𝑒𝑛𝑡, 𝑐𝑜𝑠𝑡, 1
Por lo que:
||𝑟´(𝑡)||= −𝑠𝑒𝑛𝑡 2 + 𝑐𝑜𝑠2𝑡 + 12
= 𝑠𝑒𝑛2𝑡 + 𝑐𝑜𝑠2
𝑡 + 1 = 2
Y como:
𝑓 𝑟 𝑡 = 𝑐𝑜𝑠2
𝑡 + 𝑠𝑒𝑛2
𝑡 + 𝑡2
= 1 + 𝑡2
Entonces: 𝑥2
+ 𝑦2
+ 𝑧2
𝑑𝑠 = 0
2𝜋
1 + 𝑡2
2𝑑𝑡 = √2(𝑡 +
𝑡3
3
)|
2𝜋
0
=
2 2𝜋 (3+4𝜋2)
3

EJEMPLO 2.-
Integral de línea de un campo escalar
Demostremos que la longitud de una circunferencia de radio r es 2𝜋𝑟, es decir, buscamos hallar:
𝑑𝑠
Siendo C la longitud de una circunferencia de radio r.
Por simplicidad, consideremos una circunferencia de radio r centrada en el origen, por lo que una
posible parametrización es:
𝑟 𝑡 = 𝑟𝑐𝑜𝑠 𝑡, 𝑟 𝑠𝑒𝑛 𝑡 0 ≤ 𝑡 ≤ 2𝜋
Dado que: 𝑟´ 𝑡 = (−𝑟 𝑠𝑒𝑛 𝑡, 𝑟 cos 𝑡)
𝑟´ 𝑡 = 𝑟2𝑠𝑒𝑛2𝑡 + 𝑟2𝑐𝑜𝑠2𝑡
= 𝑟2 𝑠𝑒𝑛2𝑡 + 𝑐𝑜𝑠2𝑡 = 𝑟
Por lo tanto: L(C)= 𝑐
𝑑𝑠
0
2𝜋
𝑟𝑑𝑡 = 2𝜋𝑟

EJEMPLO 3.-
Integral de línea de campos escalares
Para trayectorias r: [a,b]→𝑅𝑛
que satisfagan 𝑟´
𝑡 ≠ 0, ∀𝑡 ∈ 𝑎, 𝑏 si
𝑇 𝑡 =
𝑟´(𝑡)
||𝑟´(𝑡)||
Denota un vector tangente unitario a C entonces:
𝐹. 𝑑𝑟 =
𝑎
𝑏
𝐹 𝑟 𝑡 . 𝑟´ 𝑡 𝑑𝑡
=
𝑎
𝑏
[𝐹 𝑟 𝑡 .
𝑟´ 𝑡
𝑟´ 𝑡
]||𝑟´(𝑡)||𝑑𝑡
=
𝑎
𝑏
[𝐹 𝑟 𝑡 . 𝑇(𝑟)]||𝑟´(𝑡)||𝑑𝑡
= 𝐹. 𝑇𝑑𝑠 = 𝑓𝑑𝑠
Donde 𝑓 = 𝐹. 𝑇, por lo tanto : 𝐹. 𝑑𝑟 = 𝐹. 𝑇 𝑑𝑠

5.9 DIVERGENCIA, ROTACIONAL, INTERPRETACIÓN
GEOMÉTRICA Y FÍSICA.
Divergencia
Sea F un campo vectorial definido en un conjunto abierto Ω 𝑅𝑛 y consideremos sus coordenadas
F= 𝐹1, 𝐹2, … , 𝐹𝑛 . Supongamos F es diferenciable en un punto 𝜕𝜖Ω, lo que sabemos equivale a que
todos los campos escalares Fk, con k=1,2,…n, sean diferenciables en el punto a. Pues, bien, la traza
de dicha matriz es, por definición, la divergencia del campo F en el punto a, y se denota por
divF(a). Así pues se tendrá:
𝑑𝑖𝑣𝐹 𝑎 =
𝜕𝐹1
𝜕𝑥1
a +
𝜕𝐹2
𝜕𝑋2
𝑎 + ⋯ +
𝜕𝐹𝑛
𝜕𝑥𝑛
=
𝑘=1
𝑛
𝜕𝐹𝑘
𝜕𝐹𝑘
𝑎
Para un campo vectorial plano (x,y)7→ 𝐹 𝑥, 𝑦 = 𝑃 𝑥, 𝑦 , 𝑄 𝑥, 𝑦 , que sea diferenciable en un punto
(x0,y0) tendremos:
𝑑𝑖𝑣𝐹 𝑥0𝑦0 =
𝜕𝑝
𝜕𝑥
𝑥0, 𝑦0 +
𝜕𝑄
𝜕𝑦
𝑥0, 𝑦0
Rotacional
Rotacional en el espacio. Sea F=(P,Q,R) un campo vectorial definido en un abierto Ω 𝑅3 y
diferenciable en un punto a 𝜖Ω. Del mismo modo que la divergencia divF(a) se obtiene como el
producto escalar simbólico ∇. 𝐹 𝑎 𝑜 ∇𝑥𝐹 𝑎 . Así pues:
𝑟𝑜𝑡 𝐹 𝑎 = ∇𝑥 𝐹 𝑎 = |

5.9 DIVERGENCIA, ROTACIONAL, INTERPRETACIÓN
GEOMÉTRICA Y FÍSICA.
Rotacional
Rotacional en el espacio. Sea F=(P,Q,R) un campo vectorial definido en un abierto Ω 𝑅3 y
diferenciable en un punto a 𝜖Ω. Del mismo modo que la divergencia divF(a) se obtiene como el
producto escalar simbólico ∇. 𝐹 𝑎 𝑜 ∇𝑥𝐹 𝑎 . Así pues:
𝑟𝑜𝑡 𝐹 𝑎 = ∇𝑥 𝐹 𝑎 = |
𝑖
𝜕
𝑗
𝑘
𝜕
𝜕𝑥 𝜕𝑦 𝜕𝑧
𝑝(𝑎) 𝑄(𝑎) 𝑅(𝑎)
=
𝜕𝑅
𝜕𝑦
𝑎 −
𝜕𝑄
𝜕𝑧
𝑎 𝑖 +
𝜕𝑝
𝑎𝑧
𝑎 −
𝜕𝑅
𝜕𝑥
𝑎 𝑗 +
𝜕𝑄
𝑎𝑥
𝑎 −
𝜕𝑝
𝜕𝑥
𝑎 𝑘

EJEMPLO 1.-
• Sea el campo vectorial F(x,y,z)=(0, cos (x2), -sen(x,y)) determine su rotacional.
Solución: Al aplicar la definición de rotacional se obtiene el siguiente vector que lo representa.
𝑟𝑜𝑡 𝐹 =
𝜕
𝑎𝑦
−𝑠𝑒𝑛 𝑥𝑦 −
𝜕
𝑎𝑧
cos 𝑥𝑧 +
𝜕
𝜕𝑧
0 −
𝜕
𝜕𝑥
−𝑠𝑒𝑛 𝑥𝑦 +
𝜕
𝜕𝑥
cos 𝑥2 −
𝜕
𝑎𝑦
0
= −𝑥𝑐𝑜𝑠 𝑥𝑦 + 𝑥𝑠𝑒𝑛 𝑥𝑧 + 𝑦𝑐𝑜𝑠 𝑥𝑦 + −𝑧𝑠𝑒𝑛 𝑥𝑧
= 𝑥 𝑠𝑒𝑛 𝑥𝑧 − cos 𝑥𝑦 + 𝑦 cos 𝑥𝑦 − 𝑧𝑠𝑒𝑛(𝑥𝑧)

EJEMPLO 2.-
• Demuestre que cualquier campo vectorial definido por F(x,y,z)= (f(x),g(y),h(z)), donde f,g,h,
son funciones derivables, es irrotacional.
Solución: Se dice que un campo vectorial es irrotacional si se demuestra que 𝑟𝑜𝑡 𝐹 = 0→
, al
aplicar la definición el rotacional se obtiene:
𝑟𝑜𝑡 𝐹 =
𝜕
𝜕𝑦
ℎ 𝑧 −
𝜕
𝜕𝑧
𝑔 𝑦 𝑖 +
𝜕
𝜕𝑧
𝑓 𝑥 −
𝜕
𝜕𝑥
ℎ 𝑧 𝑗 +
𝜕
𝜕𝑥
𝑔 𝑦 −
𝜕
𝜕𝑦
𝑓 𝑥 𝑘
= 0𝑖 + 0𝑗 + 0𝑘
Por lo que se puede afirmar que el campo es irrotacional.

EJEMPLO 3.-
• Sea el campo vectorial F(x,y,z)= (𝑒𝑥𝑠𝑒𝑛 𝑦 , 𝑒𝑥 cos 𝑦 , 𝑧) determine su divergencia.
• Solución:
𝑑𝑖𝑣 𝐹 =
𝜕
𝜕𝑥
𝑒𝑥
𝑠𝑒𝑛 𝑦 +
𝜕
𝜕𝑦
(𝑒𝑥
cos 𝑦 ) +
𝜕
𝜕𝑧
(𝑧)
= 𝑒𝑥𝑠𝑒𝑛 𝑦 − 𝑒𝑥𝑠𝑒𝑛 𝑦 + 1 = 1

5.10 TEOREMAS DE INTEGRALES. APLICACIONES.
Teorema de Green. Sea C una curva dada por la parametrización:
𝑟: [𝑎, 𝑏] → ∁𝑐𝐼𝑅3
𝑡 → 𝑟 𝑡 = 𝑥 𝑡 , 𝑦 𝑡 , 𝑧 𝑡
Se dice que la curva es cerrada si r(a)=r(b).C se dice que es una curva simple si r es inyectiva en (a,b),
es decir, si: r(t1)≠r(t2) cuando a≤ 𝑡1 ≤ 𝑡2 ≤ 𝑏
Teorema de Green. Sea C una curva en el plano cerrada simple suave atrozos y orientada
positivamente. Si P(x,y) y Q(x,y) son dos funciones reales de clase e 𝐶1
, entonces:
𝑷𝒅𝒙 + 𝑸𝒅𝒚 =
𝑫
(
𝝏𝑸
𝝏𝒙
−
𝝏𝒑
𝝏𝒚
)𝒅𝒙𝒅𝒚

5.10 TEOREMAS DE INTEGRALES. APLICACIONES.
Teorema de Stokes. Dado un campo vectorial 𝐹 𝑒𝑛 𝐼𝑅3
cuyos componentes F1,F2,F3 tienen derivadas
parciales, que denotaremos por rotF, entonces:
𝑟𝑜𝑡 𝐹 =
𝜕𝐹3
𝜕𝑦
,
𝜕𝐹2
𝜕𝑧
,
𝜕𝐹1
𝜕𝑧
−
𝜕𝐹3
𝜕𝑥
−
𝜕𝐹2
𝜕𝑥
−
𝜕𝐹1
𝜕𝑦
El calculo rotacional se puede hacer de forma sencilla mediante la expresión simbólica: 𝑟𝑜𝑡 𝐹 =
∇ 𝑓 =
Teorema de divergencia Gauss. Dado un campo vectorial F de I𝑅3
cuyos componentes F1,F2,F3
tienen derivadas parciales, se define la divergencia de F, que demostraremos por divF, como el
campo escalar:
𝑑𝑖𝑣 𝐹 =
𝜕𝐹1
𝜕𝑥
+
𝜕𝐹2
𝜕𝑦
+
𝜕𝐹3
𝜕𝑍
𝑖 𝑗 𝑘
𝜕
𝜕𝑥
𝜕
𝜕𝑦
𝜕
𝜕𝑧
𝑓1 𝑓2 𝑓3

Solución
La gráfica indica la región encerrada por la curva C.
Tenemos:
𝑃 𝑥; 𝑦 = 𝑥4
→
𝜕𝑝
𝜕𝑦
= 0
𝑄 𝑥; 𝑦 = 𝑥𝑦 →
𝜕𝑄
𝜕𝑋
= 𝑦
Por lo tanto;
𝑐
𝑥4
𝑑𝑥 + 𝑥𝑦𝑑𝑥 = 𝐷
𝜕𝑄
𝜕𝑥
−
𝜕𝑝
𝜕𝑦
𝑑𝐴 = 0
1
0
1−𝑥
𝑦𝑑𝑦𝑑𝑥 = 0
1
(
1
2
𝑦2
|
1 − 𝑥
0
) 𝑑𝑥 = 0
1 1
2
(1 − 𝑥)2
𝑑𝑥 = −
1
6
(1 − 𝑥)3
|
1
0
=
1
6
EJEMPLO 1.-
Teorema de Green.
• Transformación de una integral de línea en una de área. Evaluar 𝑐
𝑥4𝑑𝑥 + 𝑥𝑦𝑑𝑥, donde C es la
curva triangular que une los puntos (0;0),(0;1) y (1;0), orientada positivamente.

EJEMPLO 2.-
Teorema de Stoke.
• Verificar el teorema de Stokes para el campo vectorial F(x;y;z)=3yi+ 4zj-6xk= 9-𝑥2
− 𝑦2
ubicada
sobre el plano xy y orientada hacia arriba.
Solución. La curva C es en este caso una circunferencia de radio 3 centrada en el origen sobre el
plano xy. Podemos parametrizarla como:
Con esta parametrización tenemos:
𝐹 𝜃 = 9 𝑆𝑒𝑛𝜃𝑖 + 0𝑗 − 18 𝑐𝑜𝑠𝜃𝑘
𝑟´ 𝜃 = −3𝑠𝑒𝑛𝜃𝑖 + 3 𝑐𝑜𝑠𝜃𝑗 + 0𝑘
𝑟´ 𝜃 = −27𝑠𝑒𝑛2
𝜃
𝐹. 𝑑𝑟 =
0
2𝜋
𝐹 𝜃 . 𝑟´ 𝜃 𝑑𝜃 =
0
2𝜋
−27 𝑠𝑒𝑛2
𝜃𝑑𝜃 =
0
2𝜋
−27
1 − 𝑐𝑜𝑠2𝜃)
2
𝜃𝑑𝜃 =
= −
27
2
𝜃 −
𝑠𝑒𝑛2𝜃
2
|
2𝜋
0
= −27𝜋

EJEMPLO 3.-
Teorema de divergencia de Gauss.
• Deseamos evaluar 𝜕𝑠
𝐹. 𝑑𝑠
donde 𝜕𝑠 es la esfera unitaria descrita por
𝜕𝑠 = {(𝑥, 𝑦, 𝑧) ∈ 𝑅3: 𝑥2 + 𝑦2 + 𝑧2 = 1}
Y F(x,y,z)= 2𝑥𝑖 + 𝑦2
𝑗 + 22
𝑘
Por lo que: 𝑎𝑠
𝐹. 𝑑𝑠 = 𝑠
∇. 𝐹 𝑑𝑣
=2 𝑠
1 + 𝑦 + 𝑧 𝑑𝑣 =2 𝑠
𝑑𝑣 + 2 𝑠
𝑦𝑑𝑣2 𝑠
𝑧𝑑𝑣
Donde S es la bola unitaria dada por
𝑠 = {(𝑥, 𝑦, 𝑧) ∈ 𝑅3: 𝑋2 + 𝑦2 + 𝑧2 ≤ 1}
Dado que la función y es positiva en un hemisferio de S y negativo en el otro entonces la integral
sobre S vale cero, similarmente para la función Z, esto es:
𝑠
𝑦𝑑𝑣 =
𝑠
𝑧𝑑𝑣 = 0
Por lo que: 𝑠
𝐹. 𝑑𝑠 = 𝑠
∇. 𝐹 𝑑𝑣 = 2 𝑠
𝑑𝑣 = 2
4𝜋
3
=
8𝜋
3

PRESENTACION GRUPAL CALCULO VECTORIAL UNIDAD 5.pptx

Más contenido relacionado

La actualidad más candente

Similar a PRESENTACION GRUPAL CALCULO VECTORIAL UNIDAD 5.pptx

Último

PRESENTACION GRUPAL CALCULO VECTORIAL UNIDAD 5.pptx