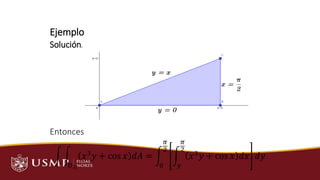
El documento introduce el concepto de integrales dobles como una extensión de las integrales definidas de una variable para calcular el volumen bajo una superficie y encima de una región del plano. Explica que las integrales dobles representan el límite de la suma de Riemann de pequeños prismas de altura f(x,y) y base un subrectángulo de la partición, al refinar la partición. Ilustra el cálculo de una integral doble iterada y de una integral doble para estimar el volumen de un sólido.