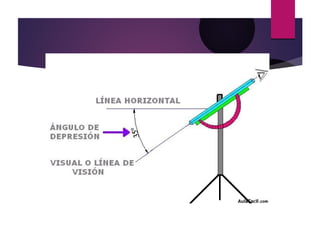
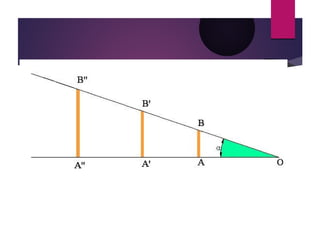
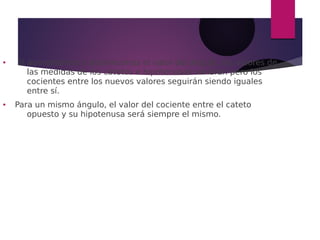
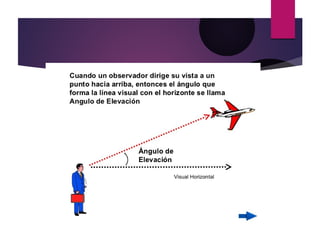
Este documento explica los ángulos de elevación y depresión, así como el seno y coseno de un ángulo. Define los ángulos de elevación y depresión como aquellos formados por dos líneas imaginarias llamadas línea visual y línea horizontal, cuando el observador se encuentra por debajo u por encima del objeto observado. Luego explica que los egipcios descubrieron que para triángulos rectángulos con el mismo ángulo, la relación entre el cateto opuesto y la hipotenusa es siempre la misma, y define esta

1. INSTITUTO NACIONAL DE SAN RAFAEL
ALUMNA: ALISON NOELY HERNANDEZ
MATERIA: MATEMATICA

2. Ángulos de Elevación y Depresión,
Seno y Coseno de un Ángulo
●
Son ángulos formados por dos líneas imaginarias
llamadas: línea visual o línea de visión y la línea
horizontal.
●
En estos casos, el observador se encuentra por
debajo del objeto observado o bien, se encuentra
por encima de dicho objeto.
●
Para estas mediciones se utilizan sencillos aparatos
que colocados sobre un trípode ( 3 puntos
determinan un solo plano) el simple giro realizado
de la mirilla sobre el punto a observar nos señala
los grados girados respecto a la horizontal:

3. TRIGOMETRIA

●
En el caso del ángulo de depresión, el observador se encuentra
por encima del lugar a observar y del modo anterior su
representación podemos hacerla del modo siguiente:

5. SENO y COSENO DE UN ÁNGULO
●
No te preocupes de las palabras que se utilizan en Trigonometría,
lo importante es que sepas para qué sirven. Comprobarás que
es una parte de las Matemáticas sencilla y muy interesante.
●
●
Los egipcios hace muchos años se dieron cuenta de que si
clavaban en el suelo unas estacas de diferentes alturas
sucedían cosas interesantes.
●
●
Observa la figura siguiente:

7. ●
Verás que tenemos tres triángulos rectángulos
● trigonometría
● Los catetos opuestos al ángulo α son, de menor a
mayor: AB, A’B’ y A”B”.
● Los catetos contiguos al ángulo α (que están tocando al
ánguloα) son, de menor a mayor: OA, O A’ y OA”.
● Las hipotenusas de los tres triángulos son, de menor a
mayor: OB, OB’ y OB”.
● Hace poco has leído que los egipcios se dieron cuenta,
pero ¿de qué se dieron cuenta?

8. ● Lee con mucha atención:
● Para un mismo ángulo α, los cocientes de los valores:

9. ● Es decir, los cocientes de los catetos opuestos al ángulo entre los
valores de sus hipotenusas, SON IGUALES.
●

10. ● Si aumentamos o disminuimos el valor del ángulo, los valores de
las medidas de los catetos e hipotenusas variarán pero los
cocientes entre los nuevos valores seguirán siendo iguales
entre sí.
● Para un mismo ángulo, el valor del cociente entre el cateto
opuesto y su hipotenusa será siempre el mismo.

11. ● Ejemplos:
●
● Para un ángulo de 30º, el cociente entre el cateto opuesto y su
hipotenusa vale 0,5.
●
● Para un ángulo de 45º, el cociente entre el cateto opuesto y su
hipotenusa vale 0,707.
●
●

12. ● Al cociente del cateto opuesto al ángulo entre su hipotenusa se
llama seno del ángulo y se escribe sen α.
●

13. EJEMPLOS ILUSTRADOS EN IMAGENES