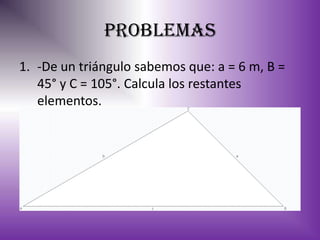
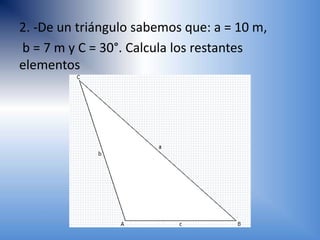
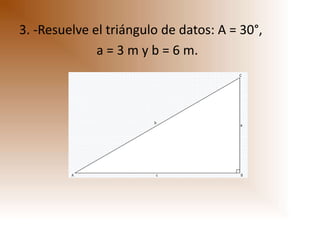
Este documento presenta información sobre trigonometría. Explica que la trigonometría estudia las relaciones entre los lados y ángulos de los triángulos. Luego, describe las funciones trigonométricas básicas como seno, coseno y tangente y cómo se definen en un triángulo rectángulo. Finalmente, muestra algunos ejemplos de aplicaciones de las funciones trigonométricas para resolver problemas geométricos.

1. TRIGONOMETRIA
TELLER DE REFUERZO
PRESENTADO POR
BAIRON ANDRES LOPEZ
MELISA CRUZ
INGRID ORTEGA

2. trigonometría
Trigonometría, rama de las matemáticas que estudia las
relaciones entre los lados y los ángulos de los triángulos.
Etimológicamente significa ‘medida de triángulos’. Las
primeras aplicaciones de la trigonometría se hicieron en
los campos de la navegación, la geodesia y la astronomía,
en los que el principal problema era determinar una
distancia inaccesible, es decir, una distancia que no podía
ser medida de forma directa, como la distancia entre la
Tierra y la Luna. Se encuentran notables aplicaciones de
las funciones trigonométricas en la física y en casi todas
las ramas de la ingeniería, sobre todo en el estudio de
fenómenos periódicos, como el flujo de corriente alterna.
Las dos ramas fundamentales de la trigonometría son la
trigonometría plana y la trigonometría esférica.

3. Razones trigonométricas de
un triangulo rectángulo.
Para establecer las razones trigonométricas, en
cualquier triángulo rectángulo, es necesario
conocer sus elementos.
hipotenusa
Cateto opuesto
adyacente

4. Los triángulos rectángulos cumplen una
serie de relaciones métricas importantes
entre sus lados. Los lados de un
triángulo rectángulo que forman
el ángulo recto, B y C, se llaman catetos y el
tercer lado, A, (opuesto al ángulo recto) es la
hipotenusa. Los ángulos con vértice
en A y B son ángulos agudos, el ángulo con
vértice en C es recto. En un triangulo
rectángulo, las razones trigonométricas del
Angulo α con vértice en A son:

5. Seno
En un triángulo rectángulo, el seno de un ángulo
agudo α, que se designa por sen α, es igual a la
longitud del cateto opuesto al ángulo dividida
por la longitud de la hipotenusa. la razón
trigonométrica es entre el cateto opuesto y la
hipotenusa.
cateto opuesto
hipotenusa

6. Coseno
En un triángulo rectángulo, el coseno de un
ángulo agudo α, que se designa por cos α, es
igual a la longitud del cateto adyacente al ángulo
dividida por la longitud de la hipotenusa.
la razón trigonométrica es entre el cateto
adyacente y la hipotenusa.
adyacente
hipotenusa

7. Tangente
En un triángulo rectángulo, la tangente de un
ángulo agudo α, que se designa por tang α, es
igual a la longitud del cateto opuesto al ángulo
dividida por la longitud del cateto adyacente.
la razón trigonométrica es entre
cateto opuesto y adyacente.
cateto opuesto
cateto adyacente

8. Razones trigonométricas
reciprocas

9. A partir de las razones trigonométricas sen, cos
y tang se definen la cosecante (cosec), la secante
(sec) y la cotangente (cot) A cada razón
fundamental corresponde una razón
recíproca, llamadas así por que cada una es la
inversa de otra.
Las tres siguientes son las razones recíprocas
que se pueden establecer respecto al mismo
ángulo.

10. cosecante
es la razón entre la hipotenusa y el cateto
opuesto al ángulo, y como es la recíproca del
seno de α se puede expresar como.

11. secante
es la razón entre la hipotenusa y el cateto
adyacente al ángulo, y como es la reciproca del
coseno de α se puede expresar como.

12. cotangente
es la razón entre el cateto adyacente al ángulo y
el cateto puesto al mismo, y como es la recíproca
de la tangente de α se puede expresar como.

13. APLICACIONES EN LAS FUNCIONES
TRIGONOMETRICAS
Hallar la longitud de
una escalera recargada
en una pared de
4,33m de altura que
forma un Angulo de 60
grados con respecto al
piso.

14. procedimiento
a) Trazar el triangulo rectángulo anotando los
datos e indicando, con una letra, el lado que se
desea calcular.
b) Seleccionar una razón trigonométrica que
relacione al ángulo y lado conocidos con el lado
que se desea calcular.

15. c) Despejar algebraicamente la letra que
representa el lado que se desea calcular.
d) Sustituir las literales por sus valores
numéricos de acuerdo con los datos.

16. e) Obtener el valor natural del Angulo por medio
de las tablas trigonométricas o de la calculadora
y efectuar las operaciones.
f) Dar solución al problema
c = longitud de la escalera
c=5m

17. 2. -problema
Hallar los ángulos de
elevación de N y M, si
estoy en una posición
de 12m del árbol con la
mirada angular de 60º
y la altura del árbol de
13,795497548672m.

19. Triangulo oblicuángulos
Los teoremas del seno y del coseno permiten
resolver triángulos oblicuángulos. Por ejemplo,
si se quiere conocer el lado c de un triángulo del
que se conocen los otros dos lados a y b, y el
ángulo, C, opuesto al lado desconocido, el
teorema del coseno permite calcularlo:
c2 = a2 + b2 – 2ab·cos C

20. problemas
1. -De un triángulo sabemos que: a = 6 m, B =
45° y C = 105°. Calcula los restantes
elementos.

21. A: Suma de los ángulos de un triangulo
A+B+C=180
b: teorema del seno: b/sin(B)= a/sin(A)
c: teorema del seno: c/sin(C)= a/sin(A)
Ángulos
SEN A=180º-(45º+105º)
SEN A=180º-150º
SEN A=30º
LADOS
b:
c:

22. 2. -De un triángulo sabemos que: a = 10 m,
b = 7 m y C = 30°. Calcula los restantes
elementos

23. ángulos
A:
B:
LADOS
c:

24. 3. -Resuelve el triángulo de datos: A = 30°,
a = 3 m y b = 6 m.

25. ángulos
B: 90
C: 60
LADOS
c:

26. 4. -Resuelve el triángulo de datos: A = 60°,
a = 8 m y b = 4 m.

27. ángulos
B:
C:
lados
c:

28. 5. -Resuelve el triángulo de datos: a = 15 m,
b = 22 m y c = 17 m.

29. Ángulos
A:
B:
C: