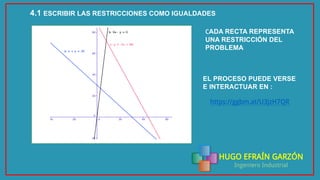
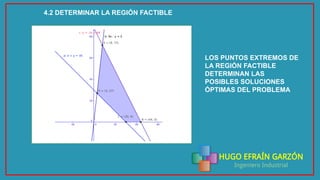
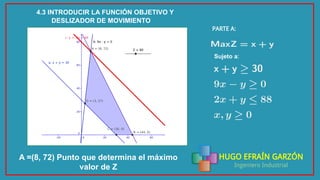
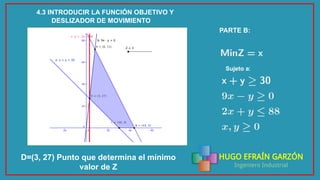
Este documento presenta la solución a un problema de programación lineal utilizando el software Geogebra. El problema involucra determinar la cantidad óptima de computadores portátiles y de escritorio que una empresa debe comprar dentro de un presupuesto, cumpliendo ciertas restricciones. El documento explica el planteamiento matemático del problema, los pasos para resolverlo en Geogebra, y las conclusiones de la solución óptima para maximizar la cantidad de computadores comprados y para minimizar la cantidad de portátiles comprados.

1. HUGO EFRAÍN GARZÓN
Ingeniero Industrial
http://rihelmio.blogspot.com.co

2. HUGO EFRAÍN GARZÓN
Ingeniero Industrial
SOLUCIÓN DE UN
PROBLEMA DE
PROGRAMACIÓN
LINEAL CON
GEOGEBRA

3. HUGO EFRAÍN GARZÓN
Ingeniero Industrial
TABLA DE CONTENIDO
ÍTEM TEMA
1. Introducción
2. Presentación del problema
3. Planteamiento del problema de Programación Lineal
4. Los pasos de la solución GEOGEBRA
5. Respuesta al problema planteado
6. Conclusiones
7. Bibliografía

4. HUGO EFRAÍN GARZÓN
Ingeniero Industrial
INTRODUCCIÓN
En esta oportunidad presento un excelente problema
de progrmación lineal, que originalmente lo
encontramos en las pruebas PAU de la Universidad de
OVIEDO, y que es de gran ayuda para un docente en
c u a l q u i e r c u r s o d e P r o g r a m a c i ó n L i n e a l o
Investigación Operativa en el momento de trabajar una
solución utilizando el software de GEOGEBRA.
Con el desarrollo de este problema se pretende
mostrar al estudiante un paso a paso desde la
formulación, pasando por la graficación en Geogebra y
finalmente llegar a la interpretación de la solución
obtenida y la redacción de la respuesta al problema.
Espero sea de gran utilidad para todos aquellos
estudiantes que están iniciando en el aprendizaje de
esta interesante temática.
1.

5. HUGO EFRAÍN GARZÓN
Ingeniero Industrial
2.
Una empresa quiere decidir cuántos ordenadores portátiles y cuántos de sobremesa
comprará. Dispone de hasta 88.000 euros y ha aceptado la oferta de un proveedor que le
exige comprar por lo menos 30 ordenadores y que al menos un 10% de los que compre
sean portátiles. Cada ordenador portátil le sale por 2.000 euros y cada uno de sobremesa
por 1.000
1. ¿Qué combinaciones de ordenadores de cada tipo puede comprar? Plantea el
problema y representa gráficamente el conjunto de soluciones.
2. Si se quiere comprar el mayor número posible de ordenadores, ¿cuántos de cada tipo
ha de comprar? ¿Y si lo que quiere es comprar el menor número posible de portátiles,
cuántos de cada tipo tendría que comprar?
PROBLEMA MEZCLA DE COMPRA DE COMPUTADORES

6. HUGO EFRAÍN GARZÓN
Ingeniero Industrial
3.
DEFINIR LAS VARIABLES DE DECISIÓN
x = Cantidad de ordenadores portátiles a comprar
y = Cantidad de ordenadores de sobremesa a comprar
PLANTEAMIENTO DEL PROBLEMA DE PL

7. HUGO EFRAÍN GARZÓN
Ingeniero Industrial
PLANTEAMIENTO DEL PROBLEMA
Planteamiento inicial
Sujeto a:
Planteamiento Final
Sujeto a:
3.

8. HUGO EFRAÍN GARZÓN
Ingeniero Industrial
SOLUCIÓN GEOGEBRA4.
La solución de un problema de programación
lineal con el software de GEOGEBRA, tiene los
siguientes pasos para la parte A y B del
problema:
1. Escribir en la barra de entrada las
restricciones como igualdades
2. Establecer la región factible, señalando los
puntos extremos con sus respectivas
coordenadas.
3. Escribir la Función objetivo igualada a cero
4. Abrir un deslizador y enlazarlo a la función
objetivo, permitir su movimiento.
5. Observar el mayor valor de la Función objetivo y
dterminar las coordenadas del punto.
A continuación desarrollamos cada uno de los
pasos:

9. HUGO EFRAÍN GARZÓN
Ingeniero Industrial
4.1 ESCRIBIR LAS RESTRICCIONES COMO IGUALDADES
CADA RECTA REPRESENTA
UNA RESTRICCIÓN DEL
PROBLEMA
EL PROCESO PUEDE VERSE
E INTERACTUAR EN :
https://ggbm.at/U3jzH7QR

10. HUGO EFRAÍN GARZÓN
Ingeniero Industrial
4.2 DETERMINAR LA REGIÓN FACTIBLE
LOS PUNTOS EXTREMOS DE
LA REGIÓN FACTIBLE
DETERMINAN LAS
POSIBLES SOLUCIONES
ÓPTIMAS DEL PROBLEMA

11. HUGO EFRAÍN GARZÓN
Ingeniero Industrial
4.3 INTRODUCIR LA FUNCIÓN OBJETIVO Y
DESLIZADOR DE MOVIMIENTO
PARTE A:
Sujeto a:
A =(8, 72) Punto que determina el máximo
valor de Z

12. HUGO EFRAÍN GARZÓN
Ingeniero Industrial
4.3 INTRODUCIR LA FUNCIÓN OBJETIVO Y
DESLIZADOR DE MOVIMIENTO
PARTE B:
Sujeto a:
D=(3, 27) Punto que determina el mínimo
valor de Z

13. HUGO EFRAÍN GARZÓN
Ingeniero Industrial
REDACTAR LA RESPUESTA AL PROBLEMA7.
PARTE A:
Si se quiere comprar el mayor número posible de ordenadores,
¿cuántos de cada tipo ha de comprar?
RESPUESTA
El mayor número de ordenadores a comprar es 80 unidades, 8
computadore portátiles y 72 Computadores de sobremesa
PARTE B:
¿Y si lo que quiere es comprar el menor número
posible de portátiles, cuántos de cada tipo tendría que
comprar?
Respuesta:
El mínimo número de portátiles que se puede comprar es
de 3, para lo cual la empresa debe comprar tambien 27
computadores de sobremesa

14. HUGO EFRAÍN GARZÓN
Ingeniero Industrial
CONCLUSIÓN8.
El problema presentado ha permitido poner en práctica algunas de las
competencias y saberes adquiridos por el estudiante no sólo en la asignatura de
Investigación de Operaciones o programación lineal, sino en otras propias de la
carrera que estén cursando.
Queda muy clara la diversidad de los problemas que el ingeniero debe resolver en
la realidad, es importante resaltar la importancia de la lectura comprensiva y crítica
para entender el problema, poder realizar el plantemaineto e interpretar la solución
del mismo.
GEOGEBRA es una excelente herramienta para encontrar soluciones a los
problemas de PL, de forma rápida y precisa, pero limitada a los problemas que
presentan únicamente dos variables.

15. HUGO EFRAÍN GARZÓN
Ingeniero Industrial
BIBLIOGRAFÍA9.
PROBLEMAS PAU UNIVERSIDAD DE OVIEDO
ASTURIAS: https://goo.gl/Mn7bP9
IMÁGNES: PIXABAY : https://pixabay.com/
GEOGEBRA PARTE I: https://ggbm.at/U3jzH7QR
GEOGEBRA PARTE 2: https://ggbm.at/HnvahxTT

16. HUGO EFRAÍN GARZÓN
Ingeniero Industrial
http://rihelmio.blogspot.com.co