Este documento describe conceptos fundamentales de geometría métrica como distancias entre puntos, puntos y planos, planos paralelos, rectas y planos paralelos, y rectas que se cruzan. Explica cómo calcular estas distancias usando productos escalares, vectoriales y mixtos. Incluye ejemplos numéricos para ilustrar cada concepto.

1. Espacio métrico

2. Espacio Métrico

3. Espacio Métrico

4. Espacio Métrico

5. Distancias entre dos puntos
 La DISTANCIA entre dos puntos P1(x1,y1,z1) y P2(x2,y2,z2) es
( ) ( ) ( ) ( )
2 2 2
1 2 2 1 2 1 2 1,d P P x x y y z z= − + − + −
( ) ( ) ( ) ( )
2 2 2
, 0 1 1 0 0 1 3d P Q = − + − + − =
 Ejemplo.- Calcular la distancia entre los
puntos P(1,0,1) y Q(0,1,0)

6. Distancias de un punto a un plano
 La DISTANCIA de un punto P(a,b,c) a un plano π : A x + B y + C z + D = 0
(utilizando el producto escalar • ) se cumplirá
·
( )
( )
( )
( ) ( )
( )1 2
1 2 3
2 2 2
2 2 2
3
cos ,
,
,
, , , ,
Siendo , , un punto del pla
n AP n AP n AP
n d P
n AP
d P
n
A B C a a b a c a
A B C
A a B b C c D
A C
A a a a
B
π
π
= × × =
= ×
⇒ = =
− − −
= =
+ +
× + × + × +
=
+ +
r uuur r uuur ruuuur
g
r
r uuur
g
r
g
no
y de la recta perpendicular que pasa por P
π
π

7. Distancias de un punto a un plano
 Ejemplo.- Calcular la distancia del punto P(3,2,-1) a un plano π : 2x-y-2z+3=0
( )
( ) ( ) ( )
( ) ( )
2 22
2 3 1 2 2 1 3
, 3
2 1 2
d P π
× + − × + − × − +
= =
+ − + −

8. Distancias entre planos paralelos
 Para calcular la distancia entre dos planos paralelos, basta con que tomemos
un punto cualquiera de un plano, y calculemos la distancia de dicho punto al
segundo plano.
 Ejemplo.- Calcular la distancia entre los planos
π1 : 9x-5y-7z+15=0
π2 : (x,y,z) = (3,3,3) + λ(1,-1,2) + µ (3,4,1)
( ) ( )
( ) ( )
( ) ( )
1 2 1 2 22
9 3 5 3 7 3 15 6
, ,
1559 5 7
d d Pπ π π
× + − × + − × +
= = =
+ − + −
Los dos planos son paralelos, ya que sus vectores normales son
proporcionales, es decir (9,-5,-7) = (-1) . (-9,5,7) = (-1).[ (1,-1,2) x (3,4,1)].
Tomando un punto de π2, por ejemplo P(3,3,3), se cumplirá

9. Distancias entre recta y plano paralelos
 Para calcular la distancia entre una recta y un plano paralelos, basta con que
tomemos un punto cualquiera de la recta, y calculemos la distancia de dicho
punto al plano.
 Ejemplo.- Calcular la distancia entre la recta y el plano
r : (x,y,z) = (1,3,-4) + λ(2,3,10)
π : 4x + 4y - 2z -3 =0
( ) ( )
( ) ( )
( )
22 2
4 1 4 3 2 4 3 7
, ,
24 4 2
d r d Pπ π
× + × + − × − −
= = =
+ + −
Dado que la recta y el plano son paralelas, ya que el producto escalar del
vector director de la recta y el vector normal es cero, es decir:
(2,3,10) • (4,4,-2) = 0
Tomando un punto de r, por ejemplo P(1,3,-4), se cumplirá

10. Distancias de un punto a una recta
 La DISTANCIA de un punto P(x0,y0,z0) a la recta r de vector director u, que
pasa por un punto A(a1,a2,a3), (utilizando el producto vectorial x ) se cumplirá
·
( )
( )
( )
( ) ( )
( )
1 2 3 0 1 0 2 0 3
2 2 2
1 2 3
1 2 3
,
,
,
, , , ,
Siendo , , un punto de la recta r
u AP u AP sen u AP
u d P r
u AP
d P r
u
u u u x a y
A a a a
a z a
u u u
× = × × =
= ×
×
⇒ = =
× − − −
=
+ +
r uuur r uuur ruuuur
r
r uuur
r
 Para hallar la distancia entre dos rectas paralelas r y s, basta con que
tomemos un punto cualquiera de P de r y hallemos d(P,r)

11. Distancias de un punto a una recta
 Ejemplo.- Calcular la distancia entre la recta y el punto
r : (x,y,z) = (2,3,4) + λ(-1,2,1)
P(3,-3,1)
( )
( ) ( )
( )
2 2 2
1,2,1 1,6,3 10
,
31 2 1
u PA
d P r
u
× − × −
= = =
− + +
r uuur
r
Dado que P(3,-3,1) no es un punto de r, como se puede comprobar
sustituyendo en la ecuación, Tomando A(2,3,4) se cumplirá

12. Distancias entre dos rectas que se cruzan
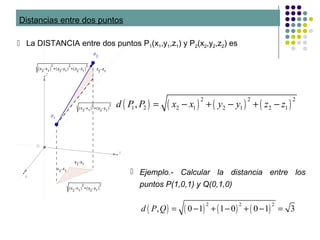
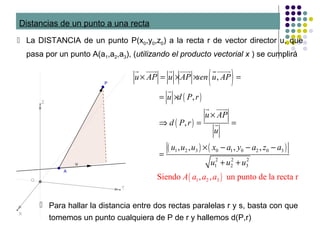
 La DISTANCIA entre dos rectas r y s, que se cruzan, (utilizando el producto
mixto [ ] ), si Pr y Ps son dos puntos cualesquiera de r y s se cumplirá
·
( )
( ) ( )
( ) ( )
( , ) cos ,
, ,
Si r y
r s r s r s
r s r s
r s
r s r s
r s r s r s r s
r s r s
d r s P P u u P P
u u P P
P P
u u P P
u u P P u u P P
u u u u
= × × =
×
= × =
× ×
 ×  
= =
× ×
uuuur uuuuuur uuuur
uuuuuur uuuur
guuuur
uuuuuur uuuur
uuuuuur uuuur uur uur uuuur
g
uuuuuur uuuuuur
s son coplanarias es , , 0r s r su u P P  = 
uur uur uuuur

13. Distancias de un punto a una recta
 Ejemplo.- Calcular la distancia entre las rectas
2 3 2
: : 5
5 2 3 2 3
x y z x z
r y s y
− + +
= = = − =
( )
( )
( )
22 2
5 2 3
2 1 3
, , 0 7 6 1 3 3
,
5 2 3
2 1 3
84 84
913 9 1
r r r s
r r
u u P P
d r s
u u i j k
  − − − − = = =
×
= =
+ − +
uur uur uuuur
uur uur r r r
Tomando Pr(7,-1,3) y Ps(0,6,3), será

14. Producto vectorial

15. Producto vectorial

16. Producto vectorial

17. Producto mixto

18. Producto mixto

19. Perpendicular común a dos rectas que se cruzan

20. Perpendicular común a dos rectas que se cruzan