El documento presenta 12 problemas resueltos sobre el cálculo de áreas de figuras planas limitadas por curvas. Se explican fórmulas para hallar el área cuando la región está limitada por una función, dos funciones, o curvas paramétricas. Los problemas aplican estas fórmulas para calcular áreas de regiones limitadas por funciones, curvas algebraicas como circunferencias e hipérbolas, y curvas como la cardioide y la astroide.

1. CAP´ITULO XI.
APLICACIONES DE LA
INTEGRAL DEFINIDA
SECCIONES
A. ´Areas de figuras planas.
B. C´alculo de vol´umenes.
C. Longitud de curvas planas.
D. Ejercicios propuestos.
37

2. A. ´AREAS DE FIGURAS PLANAS.
En Geometr´ıa Elemental se conocen las f´ormulas para hallar el ´area de cual-
quier regi´on limitada por una poligonal cerrada. Ahora bien, si una regi´on
est´a limitada por alguna l´ınea curva, como es el c´ırculo, el ´area se expresa
como un l´ımite de las ´areas de poligonales “pr´oximas”. El procedimiento
descrito en el cap´ıtulo anterior para definir el concepto de integral de una
funci´on consiste precisamente en aproximar la funci´on por funciones esca-
lonadas; si consideramos una funci´on y = f(x) no negativa en un intervalo
[a, b], la integral inferior es el l´ımite de la suma de las ´areas de los rect´angu-
los inscritos en la regi´on limitada por la curva y = f(x), el eje OX y las
rectas x = a y x = b, y la integral superior es el l´ımite de las ´areas de los
rect´angulos circunscritos a dicha regi´on. De este modo podemos definir el
´area de dicha regi´on como la integral de la funci´on f en el intervalo [a, b].
En general,
Dada una funci´on y = f(x) integrable en un intervalo [a, b], el ´area de la
regi´on limitada por la funci´on, el eje OX y las rectas x = a y x = b se define
como
A =
b
a
|f(x)| dx.
Observaci´on: El valor absoluto de la funci´on es debido a que en los inter-
valos donde la funci´on es negativa, la integral tambi´en es negativa y su valor
es opuesto al del ´area correspondiente.
En la pr´actica, para eliminar el valor absoluto en el integrando, debemos
determinar los intervalos de [a, b] donde la funci´on es positiva o negativa y
descomponer la integral en suma de integrales correspondientes a cada uno
de los intervalos indicados colocando el signo adecuado. As´ı, en la figura
adjunta, el ´area se expresa como
A =
r
a
f(x) dx −
s
r
f(x) dx +
b
s
f(x) dx.
38

3. En particular, si la funci´on est´a expresada en forma param´etrica x = x(t), y =
y(t), el ´area viene expresada como
A =
b
a
y dx =
t1
t0
y(t) · x (t) dt,
donde a = x(t0), b = x(t1).
Regiones m´as generales que las descritas son aquellas que est´an limitadas
por dos funciones y = f(x), y = g(x) entre dos rectas verticales x = a y
x = b. En este caso el ´area se expresa mediante la f´ormula
A =
b
a
|f(x) − g(x)| dx.
En el ejemplo de la figura, el ´area se descompone como:
A =
r
a
[g(x) − f(x)] dx +
s
r
[f(x) − g(x)] dx +
b
s
[g(x) − f(x)] dx.
Si la regi´on est´a limitada por dos curvas y = f(x), y = g(x) entre dos
rectas horizontales y = c e y = d, consideramos las funciones inversas
e integramos respecto a la variable y. El ´area se expresa entonces como
A =
d
c
|f−1
(y) − g−1
(y)| dy.
En el ejemplo de la figura, dicha integral se descompone como
A =
r
c
[f−1
(y) − g−1
(y)] dy +
d
r
[g−1
(y) − f−1
(y)] dy.
39

4. En los ejercicios que siguen veremos ejemplos de todas las situaciones plan-
teadas. Al ser v´alidas aqu´ı todas las propiedades de las integrales obtenidas
en el cap´ıtulo anterior, aplicaremos siempre los teoremas fundamentales de
la integral. Omitiremos en la mayor´ıa de los casos el c´alculo de las primi-
tivas pues ya se han realizado en el cap´ıtulo 7. Nos limitaremos a escribir
el resultado de dicha primitiva y a indicar las sustituciones en los extremos
de integraci´on. S´ı es muy conveniente tener una idea aproximada de la re-
presentaci´on gr´afica de las funciones involucradas para conocer la posici´on
relativa de las mismas y los intervalos de integraci´on. Es importante tam-
bi´en observar las simetr´ıas de las figuras para as´ı poder escribir f´ormulas
m´as sencillas para el ´area de las mismas.
PROBLEMA 11.1
Calcular el ´area de la regi´on limitada por la gr´afica de la funci´on
f y el eje X en el intervalo indicado:
a) f(x) = |x| − |x − 1| en [−1, 2].
b) f(x) = x(ln x)2 en [1, e].
c) f(x) = e−x| sen x| en [0, 2π].
Soluci´on
a) El ´area de la regi´on (que es la parte sombreada de la figura) viene dada
por la f´ormula A =
2
−1
|x| − |x − 1| dx.
Teniendo en cuenta el signo de la funci´on, la integral se descompone
as´ı:
A =
0
−1
1 · dx +
0,5
0
−(2x − 1) dx +
1
0,5
(2x − 1) dx +
2
1
1 · dx =
5
2
.
40

5. b) La funci´on y = x(ln x)2 es no negativa en el intervalo [1, e].
El ´area es entonces, integrando por partes,
A =
e
1
x(ln x)2
dx =
x2
2
· (ln x)2
−
x2
2
· ln x +
x2
4
e
1
=
e2 − 1
4
.
c) Nuevamente la funci´on es no negativa, por lo que A =
2π
0
e−x
| sen x| dx.
Para integrar descomponemos en dos sumandos y tenemos:
A =
2π
0
e−x
| sen x| dx =
π
0
e−x
sen x dx +
2π
π
−e−x
sen x dx
= −
e−x
2
(sen x + cos x)
π
0
+
e−x
2
(sen x + cos x)
2π
π
=
(e−π + 1)2
2
.
PROBLEMA 11.2
Hallar el ´area de la figura limitada por la funci´on f(x) = x(x −
1)(x − 2) y el eje OX.
Soluci´on
Como la curva corta al eje OX en los puntos de abscisa x = 0, x = 1 y
x = 2, el ´area viene dada por A =
2
0
|f(x)| dx.
41

6. Ahora bien, en el intervalo [0, 1] la curva queda por encima del eje X mientras
que en el intervalo [1, 2] queda por debajo del mismo. Tenemos pues
A =
1
0
f(x) dx+
2
1
−f(x) dx =
1
0
(x3
−3x2
+2x) dx−
2
1
(x3
−3x2
+2x) dx =
1
2
.
PROBLEMA 11.3
Hallar el ´area del menor de los sectores que la recta x = 3 deter-
mina en la circunferencia de ecuaci´on x2 + y2 = 25.
Soluci´on
Teniendo en cuenta la simetr´ıa de la figura basta calcular el ´area de la regi´on
contenida en el primer cuadrante. Tenemos
A = 2
5
3
25 − x2 dx
= 2
x
2
25 − x2 +
25
2
arc sen
x
5
5
3
=
25π
2
− 12 − 25 arc sen
3
5
.
42

7. PROBLEMA 11.4
Hallar el ´area de la figura limitada por la recta x = 2a y la hip´erbola
x2
a2
−
y2
b2
= 1.
Soluci´on
De acuerdo con la figura, el ´area se obtiene como
A = 2
2a
a
b (x/a)2 − 1 dx
=
bx
a
x2 − a2 − ab ln
x +
√
x2 − a2
a
2a
a
= ab[2
√
3 − ln(2 +
√
3)].
PROBLEMA 11.5
Hallar el ´area limitada por la curva y2 = x4(4 + x).
Soluci´on
Como la figura est´a determinada por el intervalo x ∈ [−4, 0] y es sim´etrica
respecto al eje X, el ´area ser´a
A = 2
0
−4
x2
√
4 + x dx = 4(4 + x)3/2 (4 + x)2
7
−
8(4 + x)
5
+
16
3
0
−4
=
4096
105
.
43

8. PROBLEMA 11.6
Hallar el ´area limitada por la curva x4 − ax3 + b2y2 = 0.
Soluci´on
La curva est´a definida cuando x ∈ [0, a] y es sim´etrica respecto a OX. El
´area viene dada por:
A = 2
a
0
x
b
ax − x2 dx = (cambio (a/2) cos t = x − a/2)
=
a3
4b
π
0
sen2
t · (1 + cos t) dt =
a3
4b
t
2
−
sen 2t
4
+
sen3 t
3
π
0
=
πa3
8b
.
PROBLEMA 11.7
Hallar el ´area de la figura limitada por la curva (x/5)2 + (y/4)2/3 =
1.
Soluci´on
El ´area de la figura, teniendo en cuenta sus simetr´ıas, es
A = 4
5
0
4(1 − x2
/25)3/2
dx = (cambio x = 5 cos t) = 16
π/2
0
5 sen4
t dt
= 20
π/2
0
(1 − cos 2t)2
dt = 20
3t
2
− sen 2t +
sen 4t
8
π/2
0
= 15π.
44

9. PROBLEMA 11.8
Hallar el ´area limitada por la curva x = (y2 + x)2.
Soluci´on
En forma expl´ıcita, la ecuaci´on de la curva es y = ±
√
x − x. Como la
gr´afica es sim´etrica respecto al eje OX, el ´area viene dada por
A = 2
1
0
√
x − x dx = (cambio
1
2
−
√
x =
sen t
2
)
=
1
2
π/2
−π/2
cos2
t · (1 − sen t) dt =
1
2
t
2
+
sen 2t
4
+
cos3 t
3
π/2
−π/2
=
π
4
.
PROBLEMA 11.9
Hallar el ´area encerrada por la curva y2
=
x2
a2
(a2
− x2
).
Soluci´on
De acuerdo con la figura y gracias a la simetr´ıa, tenemos:
A = 4
a
0
x
a
a2 − x2 dx = (cambio x = a sen t) = 4a2
π/2
0
cos2
t · sen t dt
= 4a2
−
cos3 t
3
π/2
0
=
4a2
3
.
45

10. PROBLEMA 11.10
Hallar el ´area de la figura limitada por la cardioide de ecuaci´on
x(t) = a(2 cos t − cos 2t), y(t) = a(2 sen t − sen 2t).
Soluci´on
Como la figura es sim´etrica respecto al eje OX, el ´area viene dada por
A = 2
a
−3a
y · dx = 2
0
π
y(t)x (t) dt
= 2
0
π
a(2 sen t − sen 2t)2a(sen 2t − sen t) dt
= 4a2 −3t
2
+ 2 sen3
t +
sen 2t
2
+
sen 4t
8
0
π
= 6πa2
.
PROBLEMA 11.11
Hallar el ´area comprendida entre un lazo de la cicloide x = a(t −
sen t), y = a(1 − cos t) y el eje OX.
Soluci´on
2πa
Integrando respecto a la variable t, como un lazo de la cicloide se encuentra
en el intervalo t ∈ [0, 2π], resulta:
A =
2πa
0
y(t) dx(t) =
2π
0
a(1 − cos t)a(1 − cos t) dt
= a2 3t
2
− 2 sen t +
sen 2t
4
2π
0
= 3πa2
.
46

11. PROBLEMA 11.12
Hallar el ´area encerrada por la astroide de ecuaci´on (ax)2/3 +
(by)2/3 = (a2 − b2)2/3.
Soluci´on
Escribimos la ecuaci´on en forma param´etrica como x(t) = (c2/a) cos3 t,
y(t) = (c2/b) sen3 t, donde c2 = a2 − b2.
c2/b
c2/a
Teniendo en cuenta la simetr´ıa de la figura podemos escribir el ´area co-
mo
A = 4
c2/a
0
y · dx = 4
0
π/2
(c2
/b) sen3
t · (c2
/a)(−3 cos2
t sen t) dt
=
12c4
ab
π/2
0
sen4
t cos2
t dt =
12c4
ab
t
16
−
sen 4t
64
−
sen3 2t
48
π/2
0
=
3πc4
8ab
.
PROBLEMA 11.13
Hallar el ´area de la figura limitada por la curva y3 = x, la recta
y = 1 y la vertical x = 8.
Soluci´on
47

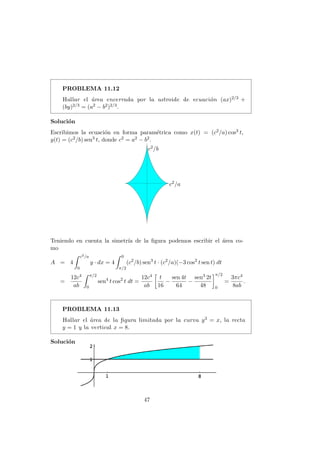
12. Como la recta y = 1 corta a la curva en el punto de abscisa x = 1 y en
el intervalo [1, 8] la curva queda por encima de la recta, el ´area viene dada
por
A =
8
1
(x1/3
− 1) dx =
3 x4/3
4
− x
8
1
=
17
4
.
PROBLEMA 11.14
Calcular el ´area limitada por la curva y = e2x y las rectas y = e2,
x = 0.
Soluci´on
En este caso, la recta y = e2 queda por encima de la curva y = e2x en la
regi´on comprendida entre los valores x = 0 y x = 1.
e2
El ´area se obtiene como
A =
1
0
(e2
− e2x
) dx = e2
x −
e2x
2
1
0
= e2
−
e2
2
+
1
2
=
e2 + 1
2
.
PROBLEMA 11.15
Hallar el ´area de la regi´on y ≥ x2 − 9, x2 + (y − 3)2 ≥ 9, y ≤ −x + 3.
48

13. Soluci´on
El centro de la circunferencia es el punto (0, 3) por el cual pasa la recta
y = −x + 3. Esto quiere decir que la recta es un di´ametro y el ´area de la
figura sombreada es la diferencia entre el ´area de la regi´on comprendida entre
dicha recta y la par´abola y el ´area del semic´ırculo de radio 3. Los puntos de
intersecci´on de la par´abola y la recta se obtienen del sistema
y = x2
− 9, y = −x + 3 =⇒ x2
+ x − 12 = 0 =⇒ x = 3, x = −4.
Tenemos entonces:
A =
3
−4
[(−x + 3) − (x2
− 9)] dx −
9π
2
=
3
−4
(−x2
− x + 12) dx −
9π
2
= 12x −
x2
2
−
x3
3
3
−4
−
9π
2
=
343
6
−
9π
2
.
PROBLEMA 11.16
Calcular el ´area de la figura limitada por las curvas y = ex, y = e−x
y la recta x = 1.
49

14. Soluci´on
Como en el intervalo x ∈ [0, 1] la curva y = ex queda por encima de la curva
y = e−x, el ´area viene dada por
A =
1
0
(ex
− e−x
) dx = ex
+ e−x 1
0
= e + e−1
− 2.
PROBLEMA 11.17
Hallar el ´area comprendida entre las par´abolas y2 = 2px, x2 = 2py.
Soluci´on
Como los puntos de intersecci´on de ambas par´abolas son (0, 0) y (2p, 2p), el
´area viene dada por la integral:
A =
2p
0
2px −
x2
2p
dx = 2p ·
2x3/2
3
−
x3
6p
2p
0
=
4p2
3
.
50

15. PROBLEMA 11.18
Dada la curva de ecuaci´on y = x3 y la recta y = λx (ver figura),
demostrar que la regi´on S1 limitada por la curva y la recta en el
intervalo x ∈ [0, a] tiene la misma ´area que la regi´on S2 limitada
por la curva y el eje X en el mismo intervalo.
Soluci´on
Como la recta pasa por el punto (a, a3), se debe cumplir que a3 = λa, es
decir λ = a2.
Al calcular cada una de las ´areas mencionadas obtenemos
S1 =
a
0
(λx − x3
) dx =
λx2
2
−
x4
4
a
0
=
2λa2 − a4
4
=
a4
4
,
S2 =
a
0
x3
dx =
x4
4
a
0
=
a4
4
,
lo que prueba el enunciado.
PROBLEMA 11.19
Hallar el ´area de la figura encerrada por la par´abola y = x2/4 y la
curva de Agnesi y =
8
x2 + 4
.
51

16. Soluci´on
Los puntos de intersecci´on de ambas curvas son soluci´on del sistema formado
por ambas ecuaciones. Tenemos que:
x2
4
=
8
x2 + 4
⇐⇒ x4
+ 4x2
= 32 ⇐⇒ x2
= −2 ±
√
4 + 32 = −2 ± 6.
Como la soluci´on x2 = −8 no es real, s´olo es posible x2 = 4 ⇐⇒ x = ±2. El
´area es entonces, teniendo en cuenta la simetr´ıa de la figura,
A =
2
−2
8
x2 + 4
−
x2
4
dx = 2
2
0
8
x2 + 4
−
x2
4
dx
= 2 4 arc tg
x
2
−
x3
12
2
0
= 2π −
4
3
.
PROBLEMA 11.20
Calcular el ´area limitada por las curvas y = x2, y = sen
πx
2
.
Soluci´on
Como se observa en la figura, la regi´on que limitan dichas curvas se encuentra
en el intervalo [0, 1] en el cual la funci´on y = sen
πx
2
queda por encima de
y = x2.
El ´area es entonces
A =
1
0
sen
πx
2
− x2
dx = −
2
π
cos
πx
2
−
x3
3
1
0
= −
1
3
+
2
π
.
52

17. PROBLEMA 11.21
Calcular el ´area de los dos trozos en que la circunferencia x2 +(y+
R)2 = 2R2 divide a la circunferencia x2 + y2 = R2.
Soluci´on
Los puntos de intersecci´on de ambas curvas son:
x2
+y2
= R2
, x2
+y2
+2Ry+R2
= 2R2
=⇒ 2Ry = 0 =⇒ y = 0 =⇒ x = ±R,
y las regiones que limitan son las indicadas en la figura.
Las ´areas de ambas regiones son:
A1 =
R
−R
R2 − x2 − 2R2 − x2 + R dx
=
x
√
R2 − x2
2
+
R2
2
arc sen
x
R
R
−R
−
x
√
2R2 − x2
2
+ R2
arc sen
x
R
√
2
R
−R
+ [Rx]R
−R = R2
;
A2 = πR2
− A1 = (π − 1)R2
.
PROBLEMA 11.22
Calcular el ´area comprendida entre las curvas y = sen3 x, y =
1/ sen x, para x ∈ [π/4, π/2].
53

18. Soluci´on
En el intervalo indicado, la curva y = 1/ sen x queda por encima de y =
sen3 x.
π/4 π/2 π
A =
π/2
π/4
1
sen x
− sen3
x dx
= ln | cosec x − cotg x| + cos x −
cos3 x
3
π/2
π/4
= − ln(
√
2 − 1) −
5
√
2
12
.
PROBLEMA 11.23
Calcular el ´area comprendida entre las curvas y = 1/ cos2 x, y =
sen6 x para x ∈ [0, π/4].
Soluci´on
En este caso tambi´en la curva y = 1/ cos2 x queda por encima de y =
sen6 x. Bastar´a pues integrar la resta de ambas funciones en el intervalo
indicado.
π/4 π/2 π
54

19. A =
π/4
0
(sec2
x − sen6
x) dx
= tg x −
5
16
x +
1
4
sen 2x −
3
64
sen 4x −
1
48
sen3
2x
π/4
0
=
59
48
−
5π
64
.
PROBLEMA 11.24
Hallar el ´area de la figura comprendida entre la hip´erbola equil´atera
x2 − y2 = 9, el eje OX y la recta que une el origen con el el punto
(5, 4).
Soluci´on
El ´area de la regi´on se puede obtener como la resta entre el ´area del tri´angulo
de v´ertices O(0, 0), A(5, 0) y B(5, 4) y el ´area de la regi´on limitada por la
hip´erbola y el eje OX en el intervalo [3, 5].
Tenemos pues:
A =
5 · 4
2
−
5
3
x2 − 9 dx
= 10 −
x
√
x2 − 9
2
−
9
2
ln
x +
√
x2 − 9
3
5
3
=
9
2
ln 3.
PROBLEMA 11.25
Determinar el ´area de la parte com´un a las dos elipses
x2
a2
+
y2
b2
= 1,
x2
b2
+
y2
a2
= 1 con a > b.
55

20. Soluci´on
Debido a la simetr´ıa de la regi´on (ver figura), basta calcular el ´area de la
regi´on comprendida en el primer cuadrante.
El punto de intersecci´on de las elipses tiene abscisa x =
ab
√
a2 + b2
, con lo
que el ´area pedida es
A = 4
ab√
a2+b2
0
b 1 − x2/a2 dx + 4
b
ab√
a2+b2
a 1 − x2/b2 dx
=
4b
a
a2
2
arc sen
x
a
+
x
2
a2 − x2
ab√
a2+b2
0
+
4a
b
b2
2
arc sen
x
b
+
x
2
b2−x2
b
ab√
a2+b2
= 2ab arc sen
b
√
a2 + b2
− arc sen
a
√
a2 + b2
+
π
2
.
PROBLEMA 11.26
Calcular el ´area de la regi´on limitada por las gr´aficas de f(x) =
|x − 1| y g(x) = x2 − 2x.
Soluci´on
Los puntos de intersecci´on de las curvas son:
y = |x − 1|, y = x2
− 2x =⇒ |x − 1| = x2
− 2x
=⇒
x − 1 = x2 − 2x si x > 1
−x + 1 = x2 − 2x si x < 1
=⇒
x = 3+
√
5
2 ,
x = 1−
√
5
2 .
56

21. Debido a la simetr´ıa de la figura, el ´area se puede expresar como:
A =
3+
√
5
2
1−
√
5
2
[|x−1|−(x2
−2x)] dx = 2
3+
√
5
2
1
[(x−1)−(x2
−2x)] dx =
7 + 5
√
5
6
.
PROBLEMA 11.27
Calcular el ´area de la figura limitada por la par´abolas y = x2,
y = x2/2 y la recta y = 2x.
Soluci´on
La primera par´abola y = x2 corta a la recta en el punto de abscisa x = 2
mientras que la segunda par´abola y = x2/2 corta a la recta en el punto de
abscisa x = 4.
El ´area se descompone entonces como suma de integrales de la siguiente
forma:
A =
2
0
(x2
− x2
/2) dx +
4
2
(2x − x2
/2) dx = 4.
57

22. PROBLEMA 11.28
Calcular el ´area de la regi´on limitada por las gr´aficas de f y g en
el intervalo que se indica en cada caso:
a) f(x) =
√
x, g(x) = x2 en [0, 2].
b) f(x) = x(x2 − 1), g(x) = x en [−1, 2].
Soluci´on
a) Los puntos de intersecci´on de las curvas son
y =
√
x, y = x2
=⇒ x = x4
=⇒ x = 0, x = 1.
El ´area se descompone entonces como la suma
A =
1
0
(
√
x − x2
) dx +
2
1
(x2
−
√
x) dx =
10 − 4
√
2
3
.
b) Los puntos de intersecci´on de las curvas son:
y = x(x2
−1), y = x =⇒ x(x2
−1) = x =⇒ x = 0, x =
√
2, x = −
√
2.
58

23. El ´area se obtiene entonces como:
A =
2
−1
|x(x2
− 1) − x| dx
=
0
−1
(x3
− 2x) dx +
√
2
0
(2x − x3
) dx +
2
√
2
(x3
− 2x) dx =
11
4
.
PROBLEMA 11.29
Calcular el ´area limitada por las regiones y ≤ x2 + 1, y ≥ x2 − 9,
y ≤ 3 − x.
Soluci´on
Calculamos los puntos de intersecci´on de las curvas:
y = x2
+ 1, y = 3 − x =⇒ x2
+ x − 2 = 0 =⇒ x = −2, x = 1;
y = x2
− 9, y = 3 − x =⇒ x2
+ x − 12 = 0 =⇒ x = −4, x = 3.
59

24. El ´area queda entonces como la suma de las siguientes integrales:
A =
−2
−4
[(3 − x) − (x2
− 9)] dx +
1
−2
[(x2
+ 1) − (x2
− 9)] dx
+
3
1
[(3 − x) − (x2
− 9)] dx
=
−2
−4
(−x2
− x + 12) dx +
1
−2
10 dx +
3
1
(−x2
− x + 12) dx =
158
3
.
PROBLEMA 11.30
Calcular el ´area comprendida entre las cuatro par´abolas
y2 = x, y2 = 2x, x2 = y, x2 = 2y.
Soluci´on
Los distintos puntos de intersecci´on son los siguientes:
x2
= 2y, y2
= x =⇒ x = 0, x = 41/3
;
x2
= y, y2
= x =⇒ x = 0, x = 1;
x2
= y, y2
= 2x =⇒ x = 0, x = 41/6
;
x2
= 2y, y2
= 2x =⇒ x = 0, x = 2.
60

25. El ´area es entonces
A =
41/6
1
[x2
−
√
x] dx +
41/3
41/6
[
√
2x −
√
x] dx +
2
41/3
[
√
2x − x2
/2] dx =
1
3
.
PROBLEMA 11.31
Calcular el ´area de la figura interior a la circunferencia x2 + (y −
1)2 = 5 y a la par´abola x = 2(y − 1)2.
Soluci´on
Los puntos de intersecci´on de ambas curvas son:
x2
+(y −1)2
= 5, x/2 = (y −1)2
=⇒ 2x2
+x−10 = 0 =⇒ x = 2, x = −5/2.
Como la par´abola est´a definida en x ≥ 0, s´olo es posible la soluci´on x = 2
lo que da los puntos (2, 0) y (2, 2).
Como debemos descomponer la integral en dos sumandos para integrar res-
61

26. pecto a la variable x, integramos respecto a y, lo que da lugar a:
A =
2
0
5 − (y − 1)2 − 2(y − 1)2
dy
=
5
2
arc sen
y − 1
√
5
+
y − 1
2
5 − (y − 1)2 −
2
3
(y − 1)3
2
0
= 5 arc sen
1
√
5
+
2
3
.
PROBLEMA 11.32
Encontrar el ´area de la regi´on com´un a las circunferencias C1 :
x2 + y2 = 4, C2 : x2 + y2 = 4x.
Soluci´on
Los puntos de intersecci´on de las circunferencias son (1,
√
3) y (1, −
√
3), de
modo que, si integramos respecto a la variable y, el ´area puede expresarse
como la integral
A = 2
√
3
0
[ 4 − y2 − (2 − 4 − y2)] dy = 4
√
3
0
( 4 − y2 − 1) dy
= 4
y
2
4 − y2 + 2 arc sen
y
2
− y
√
3
0
=
8π
3
− 2
√
3.
PROBLEMA 11.33
Sea f la funci´on indicada en la figura adjunta.
Hallar
1
0
f y tambi´en el ´area de la regi´on comprendida entre la
funci´on f y el eje X.
62

27. Soluci´on
El ´area ser´a la suma de las ´areas de los tri´angulos que la funci´on determina
con el eje OX. Resulta entonces la siguiente serie geom´etrica:
A =
∞
n=1
1
2
·
1
2n−1
−
1
2n
· 1 =
∞
n=1
1
2
·
1
2n
=
1
2
·
1/2
1 − 1/2
=
1
2
.
Para calcular la integral, debemos sumar las ´areas de los tri´angulos que que-
den por encima del eje OX y restarle la suma de las ´areas de los tri´angulos
que quedan por debajo del mismo. Tenemos nuevamente las series geom´etri-
cas,
1
0
f =
∞
n=0
1
2
·
1
22n
−
1
22n+1
−
∞
n=1
1
2
·
1
22n−1
−
1
22n
=
∞
n=0
1
22n+2
−
∞
n=1
1
22n+1
=
1/4
1 − 1/4
−
1/8
1 − 1/4
=
1
6
.
B. C´ALCULO DE VOL ´UMENES.
El concepto de integral tambi´en puede aplicarse para calcular vol´umenes de
ciertos s´olidos. Los distintos casos y m´etodos utilizados son los que expone-
mos a continuaci´on.
63

28. B.1.- VOL´UMENES DE S´OLIDOS DE SECCI´ON CONOCIDA.
Supongamos que un s´olido est´a limitado por dos planos paralelos entre s´ı y
perpendiculares a un eje fijo t en los puntos t = t0 y t = t1. Supongamos
adem´as que las secciones producidas en el s´olido por planos perpendiculares
al eje t son regiones cuya ´area se puede escribir como una funci´on A(t)
integrable en [t0, t1]. Entonces el volumen de dicho s´olido verifica la f´ormula
de Cavalieri
(1) V =
t1
t0
A(t) dt.
En particular, si las secciones son perpendiculares al eje OX entre los valores
x0 y x1, V =
x1
x0
A(x) dx.
As´ı, en el ejemplo de la figura tenemos una pir´amide de base b y altura h y
las secciones perpendiculares al eje OX son cuadrados.
Para calcular el lado de un cuadrado gen´erico escribimos la ecuaci´on de la
recta que une el origen con el punto (h, b) y calculamos su valor en el punto
de abscisa x. Resulta pues y = bx/h con lo que la funci´on a integrar ser´a el
´area del cuadrado A(x) = (2y)2 = (2bx/h)2 y el volumen es
V =
h
0
(2bx/h)2
dx =
4b2
h2
x3
3
h
0
=
4b2h
3
.
64

29. B.2.- VOL´UMENES DE S´OLIDOS DE REVOLUCI´ON.
El s´olido de revoluci´on es la figura obtenida al girar una regi´on plana al-
rededor de un eje fijo (eje de revoluci´on o eje de giro). Esto quiere decir
que las secciones perpendiculares a dicho eje son c´ırculos (o coronas circula-
res). El volumen se obtiene seg´un el caso con los siguientes m´etodos: B.2.1.-
M´ETODO DE LOS DISCOS.
Consiste en interpretar el volumen como l´ımite de la suma de los vol´umenes
de los discos que se obtienen al cortar la figura por planos perpendiculares
al eje de giro. Podemos distinguir dos casos:
(*) El eje de giro forma parte del contorno de la regi´on plana.
Si consideramos la regi´on plana limitada por la curva y = f(x), el eje de
giro y las rectas x = a, x = b, las secciones perpendiculares al eje de giro
son c´ırculos con lo que debemos integrar la funci´on que corresponda al ´area
de los mismos en el intervalo correspondiente.
As´ı, si el eje de giro es el eje OX, tenemos la f´ormula
(2) V = π
b
a
[f(x)]2
dx.
Si el eje de giro es la recta y = r, el radio del c´ırculo en un punto de abscisa
x es |f(x) − r| y el volumen queda entonces:
(3) V = π
b
a
[f(x) − r]2
dx.
En otros casos se procede de forma similar.
(**) El eje de giro no forma parte del contorno de la regi´on pla-
na.
65

30. Consideramos ahora la regi´on limitada por las curvas y = f(x), y = g(x) y
dos rectas perpendiculares al eje de giro, siendo ´este exterior a la regi´on. En
este caso, las secciones perpendiculares al eje de giro son coronas circulares.
Debemos pues restar el ´area del c´ırculo exterior menos el ´area del c´ırculo
interior.
Si el eje de giro es el eje OX,
(4) V = π
b
a
([f(x)]2
− [g(x)]2
) dx.
An´alogamente, si el eje de giro es la recta y = r,
(5) V = π
b
a
([f(x) − r]2
− [g(x) − r]2
) dx.
Ser´a necesario conocer la posici´on relativa de las funciones f y g para lo cual
es fundamental tener una idea de las gr´aficas de las mismas.
B.2.2.- M´ETODO DE LOS TUBOS.
Este m´etodo consiste en interpretar el volumen como l´ımite de la suma de
los vol´umenes de los tubos obtenidos al girar alrededor del eje de giro las
franjas de espesor infinitesimal que determina en la regi´on una partici´on del
intervalo. Este m´etodo ser´a apropiado cuando al intentar aplicar el m´etodo
de los discos se deba descomponer la integral en varios sumandos.
66

31. Como el volumen de cada uno de estos tubos es 2π· radio medio · altura, el
volumen obtenido al girar la regi´on comprendida entre la funci´on y = f(x),
el eje X y las rectas x = a, x = b tiene las siguientes f´ormulas.
Cuando el eje de giro es el eje OY :
(6) V = 2π
b
a
x · f(x) dx.
Cuando el eje de giro es la recta vertical x = r:
(7) V = 2π
b
a
|x − r| · f(x) dx.
F´ormulas an´alogas se obtienen para regiones comprendidas entre dos funcio-
nes o para ejes horizontales. En los siguientes problemas se realizan ejemplos
de todos los casos indicados.
PROBLEMA 11.34
Hallar el volumen de la figura engendrada al girar la curva y2 = x3
alrededor del eje X a lo largo del intervalo x ∈ [0, 1].
67

32. Soluci´on
De acuerdo con la figura, y aplicando la f´ormula (2), tenemos:
V = π
1
0
x3
dx = π
x4
4
1
0
=
π
4
.
PROBLEMA 11.35
Hallar el volumen del cuerpo engendrado por la rotaci´on, alrededor
del eje OX, de la superficie limitada por el eje OX y la par´abola
y = ax − x2 (a > 0).
Soluci´on
Aplicamos directamente el m´etodo de los discos integrando en el intervalo
[0, a] que corresponde a los valores de x que limitan la superficie dada.
As´ı:
V = π
a
0
(ax − x2
)2
dx = π
a
0
(a2
x2
+ x4
− 2ax3
) dx =
πa5
30
.
68

33. PROBLEMA 11.36
Calcular el volumen del s´olido engendrado por la rotaci´on de la
regi´on limitada por los ejes coordenados y la curva de ecuaci´on
√
x +
√
y =
√
a (a > 0) alrededor del eje OX.
Soluci´on
De la ecuaci´on de la curva se obtiene que y2 = (
√
a −
√
x)4 = a2 + x2 +
6ax − 4a3/2x1/2 − 4a1/2x3/2. El volumen buscado es pues
V = π
a
0
y2
(x) dx = π
a
0
(a2
+x2
+6ax−4a3/2
x1/2
−4a1/2
x3/2
) dx =
πa3
15
.
PROBLEMA 11.37
Los semiejes positivos y un cuadrante de la astroide de ecuaci´on
x = a cos3 t, y = a sen3 t delimitan una regi´on cuya ´area designare-
mos por S. Se pide:
i) El volumen del cuerpo de revoluci´on engendrado por S al girar en
torno al eje OX.
ii) El volumen del cuerpo de revoluci´on engendrado por S al girar en
torno al eje OY .
69

34. Soluci´on
i)
Por el m´etodo de los discos, si integramos respecto al par´ametro t,
como los valores extremos x = 0 y x = a corresponden a t = π/2 y
t = 0, respectivamente, tenemos:
V = π
a
0
y2
(t) dx(t) = π
0
π/2
a2
sen6
t · (−3a cos2
t sen t) dt
= 3πa3
π/2
0
sen7
t cos2
tdt=−3πa3 cos3 t
3
−
3 cos5 t
5
+
3 cos7 t
7
−
cos9 t
9
π/2
0
=
16πa3
105
ii)
Utilizaremos en este caso el m´etodo de integraci´on por tubos. El vo-
lumen es
V = 2π
a
0
x(t)y(t) dx(t) = 2π
0
π/2
a cos3
t · a sen3
t · (−3a cos2
t sen t) dt
= 6πa3
π/2
0
cos5
t sen4
t dt = 6πa3 sen5 t
5
−
2 sen7 t
7
+
sen9 t
9
π/2
0
=
16πa3
105
.
El resultado es el mismo debido a las simetr´ıas de la figura.
PROBLEMA 11.38
Hallar el volumen engendrado por la rotaci´on alrededor del eje
OY del ´area limitada por el primer arco de la cicloide de ecuaci´on
x = t − sen t, y = 1 − cos t.
70

35. Soluci´on
2π
De acuerdo con la figura, si aplicamos el m´etodo de los tubos e integramos
respecto al par´ametro t, tenemos:
V = 2π
2π
0
x(t)y(t) dx(t) = 2π
2π
0
(t − sen t)(1 − cos t)(1 − cos t) dt
= 2π
2π
0
(t − 2t cos t + t cos2
t − sen t + 2 sen t cos t − cos2
t sen t) dt
= 2π
3t2
4
− cos t +
cos3 t
3
−
3 cos 2t
8
−
7t sen t
4
2π
0
= 6π3
.
PROBLEMA 11.39
Calcular el volumen del s´olido obtenido al girar la regi´on limitada
por la curva f(x) = sen x + cos x y el eje X en el intervalo [0, π]
alrededor del eje X.
Soluci´on
Si aplicamos el m´etodo de los discos, resulta:
V = π
π
0
(sen x + cos x)2
dx = π x −
1
2
cos 2x
π
0
= π2
.
La siguiente figura da una idea de la forma del s´olido obtenido.
71

36. PROBLEMA 11.40
Se considera el ´area S de la regi´on limitada por un cuadrante de
una circunferencia de radio R y las tangentes en sus extremos.
Hallar el volumen que engendra S cuando gira en torno a una de
las tangentes.
Soluci´on
Tomamos como eje OX el eje de giro y como eje OY la recta que, pasando
por
el centro de la circunferencia, es paralela a la otra tangente. De este modo la
ecuaci´on de la circunferencia ser´a x2 + (y + R)2 = R2 =⇒ y =
√
R2 − x2 −
R.
El volumen pedido viene expresado por:
V = π
R
0
y2
(x) dx = π
R
0
( R2 − x2 − R)2
dx
= π 2R2
x −
x3
3
− R3
arc sen
x
R
R
0
=
πR3
6
(10 − 3π).
72

37. PROBLEMA 11.41
Calcular el volumen engendrado por un segmento circular de ´angu-
lo central 2α (ver figura) con α < π/2 y radio R al girar alrededor
de su cuerda.
Soluci´on
Tomando como eje OX la cuerda AB y como eje OY la perpendicular a
esta cuerda que pase por el centro de la circunferencia, debido a que OB =
R sen α y |OC| = R cos α, la ecuaci´on de la circunferencia es x2 + (y +
R cos α)2 = R2, de donde y = −R cos α +
√
R2 − x2. De esta forma, el
volumen pedido es
V = π
R sen α
−R sen α
y2
dx = 2π
R sen α
0
(R2
cos2
α + R2
− x2
− 2R cos α R2 − x2) dx
=
2πR3
3
(2 sen α − 3α cos α + cos2
α sen α).
PROBLEMA 11.42
Se considera el arco OAB de la par´abola de ecuaci´on y = x(x − a),
con OA = a > 0 y OC = c > a. Determinar c de tal manera que
el volumen de revoluci´on engendrado por la zona sombreada de la
figura, al girar en torno a OX, sea igual al volumen engendrado
por el tri´angulo OCB girando en torno al mismo eje.
73

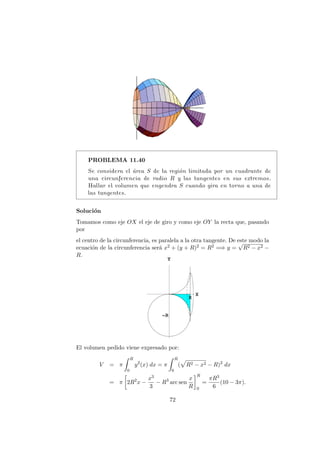
38. Soluci´on
El volumen engendrado por la zona sombreada es
V = π
a
0
y2
(x) dx + π
c
a
y2
(x) dx = π
a
0
x2
(x − a)2
dx + π
c
a
x2
(x − a)2
dx
=
πc3
30
(6c2
− 15ca + 10a2
).
Como OC = c, BC = c(c − a) y el volumen del cono engendrado por el
tri´angulo OCB es
V =
πc2(c − a)2 · c
3
=
πc3(c − a)2
3
.
Igualando los valores de V y V se deduce que c = 5a/4.
PROBLEMA 11.43
Al girar alrededor del eje OX la curva de ecuaci´on y =
√
x
1 + x2
se
obtiene en el intervalo [0, x] un s´olido cuyo volumen designaremos
por V (x). Determinar el valor de a para que V (a) =
1
2
l´ım
x→∞
V (x).
Soluci´on
El volumen V (x) se calcula mediante la f´ormula:
V (x) = π
x
0
y2
(x) dx = π
x
0
x dx
(1 + x2)2
=
π
2
−1
1 + x2
x
0
=
π
2
·
x2
1 + x2
.
74

39. Ahora bien, como l´ım
x→∞
V (x) =
π
2
, deber´a cumplirse
π
2
·
a2
1 + a2
=
1
2
·
π
2
de
donde a = 1 (no es v´alido a = −1 pues no est´a en el dominio de la funci´on).
PROBLEMA 11.44
Un s´olido de revoluci´on est´a generado por la rotaci´on de la gr´afica
de y = f(x) para [0, a] alrededor del eje X. Si para a > 0 el volumen
es a3 + a, hallar la funci´on f.
Soluci´on
Por la f´ormula del volumen tenemos que
a3
+ a = V = π
a
0
[f(x)]2
dx.
Si llamamos G a una primitiva de f2, es decir tal que G (x) = f2(x), enton-
ces
V = π[G(a) − G(0)] = a3
+ a =⇒ G(a) =
a3 + a
π
+ G(0).
Esto sugiere definir G(x) =
x3 + x
π
. De este modo, G(0) = 0 y
G (x) =
3x2 + 1
π
= f2
(x) =⇒ f(x) =
3x2 + 1
π
.
PROBLEMA 11.45
Hallar el volumen de la figura engendrada al girar la superficie
comprendida entre la par´abola y2 = x y la circunferencia y2 =
2x − x2 alrededor del eje X.
Soluci´on
Los puntos de intersecci´on de ambas curvas son (1, 1) y (1, −1).
75

40. Utilizando el m´etodo de integraci´on por discos y descomponiendo la integral
en dos sumandos, tenemos
V = π
1
0
x dx + π
2
1
(2x − x2
) dx = π
x2
2
1
0
+ π x2
−
x3
3
2
1
=
7π
6
.
PROBLEMA 11.46
Se considera la par´abola de ecuaci´on y = x2
√
2/a, con a > 0, y la
circunferencia x2+y2 = a2. Determinar el volumen engendrado por
la zona sombreada de la figura al girar en torno al eje OX.
Soluci´on
Resolviendo el sistema formado por las ecuaciones de la par´abola y de la
circunferencia, se tiene que OC = a
√
2/2. Como el radio de la circunferencia
76

41. es a, el volumen pedido ser´a
V = π
a
√
2/2
0
2x4
/a2
dx + π
a
a
√
2/2
(a2
− x2
) dx
= π
2x5
5a2
a
√
2/2
0
+ π a2
x −
x3
3
a
a
√
2/2
=
πa3
30
(20 − 11
√
2).
PROBLEMA 11.47
Determinar el volumen del s´olido obtenido al girar alrededor del
eje OY la regi´on limitada por las par´abolas y = ax2, y = b − cx2,
con a, b, c > 0.
Soluci´on
Los puntos de intersecci´on de las par´abolas se obtienen resolviendo el sistema
formado por sus ecuaciones. As´ı se tiene A( b/(a + c), ab/(a + c)).
Calculamos el volumen por el m´etodo de los discos para lo cual debemos
integrar respecto a y en los intervalos (0, ab/(a+c)) y (ab/(a+c), b). Resulta
as´ı:
V = π
ab/(a+c)
0
y
a
dy + π
b
ab/(a+c)
b − y
c
dy =
πb2
2(a + c)
.
77

42. PROBLEMA 11.48
Hallar el volumen generado por la rotaci´on del ´area limitada por
la par´abola y2 = 8x y la ordenada correspondiente a x = 2
i) en torno al eje X;
ii) en torno al eje Y ;
iii) en torno a la recta x = 2.
Soluci´on
i) Dividiendo el ´area en franjas verticales, al girar alrededor del eje X se
obtienen discos de radio y =
√
8x en el intervalo x ∈ [0, 2].
Aplicando la f´ormula de integraci´on por discos se obtiene:
V = π
2
0
8x dx = 16π.
ii) Aplicaremos nuevamente el m´etodo de los discos para lo cual debemos
integrar respecto a la variable y en el intervalo [−4, 4].
78

43. Como un disco gen´erico tiene radio exterior 2 y radio interior x = y2/8,
el volumen viene dado por
V = π
4
−4
[22
− (y2
/8)2
] dy = π 4y −
y5
320
4
−4
=
128π
5
.
iii) Aplicaremos en este caso el m´etodo de los tubos. Como se observa en
la figura, la altura de un cilindro gen´erico es 2y = 2
√
8x = 4
√
2x y su
distancia al eje de giro es 2 − x.
El volumen pedido ser´a
V = 2π
2
0
4
√
2x(2 − x) dx = 8
√
2π
2
0
(2x1/2
− x3/2
) dx =
256π
15
.
PROBLEMA 11.49
¿Cu´al es el volumen del s´olido que se obtiene al girar alrededor
del eje X la figura limitada por la curva y = ex y las rectas x = 0,
y = e?
79

44. Soluci´on
Como la recta y = e queda por encima de la curva y = ex en el intervalo
[0, 1], si aplicamos la f´ormula (4), el volumen viene dado por:
V = π
1
0
(e2
− e2x
) dx = π e2
x −
1
2
e2x
1
0
= π ·
e2 + 1
2
.
Una idea del s´olido obtenido se expresa en la siguiente figura.
PROBLEMA 11.50
Se considera la regi´on del plano formada por los puntos (x, y) que
satisfacen las desigualdades 0 ≤ x ≤ 2, x2/4 ≤ y ≤ 1. Calcular el
volumen del s´olido obtenido al girar esta regi´on alrededor del eje
Y , alrededor del eje X, alrededor de la recta x = 2, y alrededor de
la recta y = 1.
80

45. Soluci´on
a)
Al girar alrededor del eje Y , el volumen (por el m´etodo de los discos)
es
V = π
1
0
4y dy = π 2y2 1
0
= 2π.
b)
Nuevamente por el m´etodo de los discos, si integramos respecto a x,
tenemos:
V = π
2
0
1 −
x4
16
dx = π x −
x5
80
2
0
=
8π
5
.
c)
Aplicando en esta ocasi´on el m´etodo de los tubos tenemos:
V = 2π
2
0
(2 − x)(1 − x2
/4) dx = 2π 2x −
x2
2
−
x3
6
+
x4
16
2
0
=
10π
3
.
81

46. d)
Integrando por el m´etodo de los discos, tenemos por ´ultimo que
V = π
2
0
(1 − x2
/4)2
dx = π x −
x3
6
+
x5
80
2
0
=
16π
15
.
PROBLEMA 11.51
Hallar el volumen generado por la rotaci´on del ´area limitada por
y = −x2 − 3x + 6, x + y − 3 = 0 alrededor de la recta
i) y = 0;
ii) x = 3.
Soluci´on
i) Los puntos de intersecci´on de las curvas son
y = −x2
−3x+6, y = 3−x =⇒ −x2
−2x+3 = 0 =⇒ x = −3, x = 1.
82

47. Si aplicamos el m´etodo de los discos, como la par´abola queda por
encima de la recta en el intervalo x ∈ [−3, 1], el volumen es:
V = π
1
−3
(y2
p − y2
r ) dx = π
1
−3
[(−x2
− 3x + 6)2
− (3 − x)2
] dx
= π
1
−3
(x4
+ 6x3
− 4x2
− 30x + 27) dx =
1792π
15
.
ii) La recta x = 3 es exterior a la regi´on que gira. Aplicamos en este caso
el m´etodo de las tubos. La altura de un cilindro gen´erico es yp − yr =
(−x2 − 3x + 6) − (3 − x) = −x2 − 2x + 3 y el radio es 3 − x (distancia
del eje de giro a un punto de la regi´on).
El volumen es pues
V = 2π
1
−3
(3−x)(−x2
−2x+3) dx = 2π
1
−3
(x3
−x2
−9x+9) dx =
256π
3
.
PROBLEMA 11.52
Calcular el volumen del s´olido obtenido al girar la regi´on limitada
por las gr´aficas de f(x) = b(x/a)2 y g(x) = b|x/a| alrededor de y = 0.
Soluci´on
Los puntos de intersecci´on de ambas curvas son:
x ≥ 0 : y =
bx2
a2
, y =
bx
a
=⇒
bx2
a2
=
bx
a
=⇒ x2
− ax = 0 =⇒ x = 0, x = a.
83

48. Debido a la simetr´ıa de la figura, como la recta queda por encima de la
par´abola, el volumen es:
V = 2π
a
0
b2x2
a2
−
b2x4
a4
dx = 2π ·
b2
a2
x3
3
−
x5
5a2
a
0
=
4πb2 · a
15
.
PROBLEMA 11.53
Calcular el volumen engendrado por la regi´on que delimitan las
par´abolas y2 = 2px, x2 = 2py (p > 0), al girar en torno a OX.
Soluci´on
Se obtiene f´acilmente que los puntos de intersecci´on de las par´abolas son
(0, 0) y (2p, 2p).
Por el m´etodo de los discos, el volumen es:
V = π
2p
0
2px dx − π
2p
0
x4
4p2
dx =
12
5
πp3
.
PROBLEMA 11.54
Calcular el volumen del s´olido obtenido al girar la regi´on limitada
por las gr´aficas de f(x) = sen x y g(x) = cos x en el intervalo [0, π/2]
alrededor del eje X.
84

49. Soluci´on
π/4 π/2
Aplicando el m´etodo de los discos, debido a la posici´on relativa de las cur-
vas, debemos descomponer la integral en los intervalos [0, π/4] y [π/4, π/2].
As´ı tenemos:
V = π
π/4
0
(cos2
x − sen2
x) dx + π
π/2
π/4
(sen2
x − cos2
x) dx
= π
sen 2x
2
π/4
0
− π
sen 2x
2
π/2
π/4
= π.
PROBLEMA 11.55
Calcular el volumen del s´olido obtenido al girar la regi´on limitada
por las gr´aficas de f(x) = x2 − 4x + 4 y g(x) = 4 − x alrededor de
y = −1.
Soluci´on
Los extremos de integraci´on ser´an los puntos de intersecci´on de las curvas.
Estos son:
y = x2
− 4x + 4, y = 4 − x =⇒ x2
− 3x = 0 =⇒ x = 0, x = 3.
85

50. Si aplicamos el m´etodo de los discos (f´ormula (5)), teniendo en cuenta que
el radio exterior es re = yr +1 = 4−x+1 y el radio interior es ri = yp +1 =
x2 − 4x + 4 + 1, resulta:
V = π
3
0
[(4 − x + 1)2
− (x2
− 4x + 4 + 1)2
] dx
= π
x3
3
− 5x2
+ 25x −
(x − 2)2
5
− x −
2(x − 2)3
3
3
0
=
117π
5
.
Una secci´on del s´olido obtenido tiene la forma de la figura adjunta.
86

51. PROBLEMA 11.56
Determinar el volumen del s´olido que se obtiene al girar alrededor
del eje de abscisas la regi´on del primer cuadrante limitada por las
curvas y = 1/x2, y = sen(πx/2) y las rectas x = 0, y = e.
Soluci´on
Los puntos de intersecci´on de las curvas son
y = 1/x2
, y = sen
πx
2
=⇒ sen
πx
2
=
1
x2
=⇒ x = 1;
y = 1/x2
, y = e =⇒ x2
= 1/e =⇒ x = 1/
√
e.
Aplicando el m´etodo de los discos, tenemos:
V =
1/
√
e
0
π e2
− sen2 πx
2
dx +
1
1/
√
e
π
1
x4
− sen2 πx
2
dx
= π e2
x −
x
2
+
sen πx
2π
1/
√
e
0
+ π
−1
3x3
−
x
2
+
sen πx
2π
1
1/
√
e
=
(8e
√
e − 5)π
6
.
87

52. PROBLEMA 11.57
Se considera la hip´erbola de ecuaci´on x2/a2 − y2/b2 = 1 y las dos
rectas perpendiculares al eje OX de ecuaciones x = p, x = p + h
(p > a).
Determinar el volumen del cuerpo de revoluci´on engendrado por la
regi´on ABCD indicada en la figura (siendo OB una de las as´ınto-
tas) al girar en torno al eje OX.
Soluci´on
Sabiendo que la ecuaci´on de la as´ıntota OB es y = bx/a, el volumen del
s´olido indicado viene dado por
V = π
p+h
p
bx
a
2
− b2 x2
a2
− 1 dx =
πb2
a2
p+h
p
(x2
−x2
+a2
) dx = πb2
h.
PROBLEMA 11.58
Hallar el volumen generado por el ´area comprendida entre la par´abo-
la y = 4x−x2 y el eje X al girar alrededor de la recta y = 6.
88

53. Soluci´on
Utilizando el m´etodo de los discos, como la regi´on est´a comprendida en el
intervalo [0, 4], el volumen, dado por la f´ormula (5), es
V = π
4
0
[62
− (6 − y)2
] dx = π
4
0
[36 − (6 − 4x + x2
)2
] dx
= π
4
0
(48x − 28x2
+ 8x3
− x4
) dx =
1408π
15
.
PROBLEMA 11.59
Un servilletero se obtiene practicando un agujero cil´ındrico en una
esfera de modo que el eje de aqu´el pase por el centro de ´esta.
Si la longitud del agujero es 2h, demostrar que el volumen del
servilletero es πah3, siendo a un n´umero racional.
Soluci´on
Si llamamos r al radio de la esfera, el radio del agujero cil´ındrico ser´a k =√
r2 − h2.
89

54. De este modo, y de acuerdo con la figura, el s´olido obtenido viene dado al
girar alrededor del eje X la regi´on limitada por las curvas x2 + y2 = r2 e
y = k. Tenemos entonces:
V = π
h
−h
(r2
− x2
− k2
) dx = π (r2
− k2
)x −
x3
3
h
−h
=
4πh3
3
.
Como 4/3 es racional, el resultado obtenido prueba el enunciado.
Una secci´on de la figura obtenida es la siguiente:
PROBLEMA 11.60
Se considera la elipse de ecuaci´on
x2
a2
+
y2
b2
= 1 y la cuerda FC
paralela al eje OX. Determinar OA = h de manera que el volumen
engendrado por la regi´on sombreada de la figura al girar en torno a
OX sea la mitad del volumen del elipsoide engendrado por el ´area
que limita la elipse dada girando en torno al mismo eje.
90

55. Soluci´on
Designaremos por V1 y V2 a los vol´umenes del cuerpo engendrado por la
regi´on sombreada y del elipsoide engendrado por la elipse, respectivamen-
te. Como los puntos C y F tienen abscisa a 1 − h2/b2 y −a 1 − h2/b2,
respectivamente, dichos vol´umenes se obtienen por integraci´on mediante las
f´ormulas:
V1 = π
a
√
1−h2/b2
−a
√
1−h2/b2
[b2
(1 − x2
/a2
) − h2
] dx
= 2π
a
√
1−h2/b2
0
[b2
(1 − x2
/a2
) − h2
] dx = 2π (b2
− h2
)x −
b2x3
3a2
a
√
1−h2/b2
0
=
4
3
πa(b2
− h2
) 1 − h2/b2;
V2 = π
a
−a
b2
(1 − x2
/a2
) dx =
4
3
πab2
.
Como debe ser V1 = V2/2, al resolver esta ecuaci´on se obtiene que
4
3
πa(b2
− h2
) 1 − h2/b2 =
2
3
πab2
=⇒ h = b 1 − 1/
3
√
4.
PROBLEMA 11.61
Calcular el volumen del toro, que es el s´olido de revoluci´on engen-
drado al girar un c´ırculo de radio r alrededor de un eje situado en
su plano y a una distancia b de su centro (b ≥ r).
91

56. Soluci´on
Si hacemos que OX sea el eje de giro y el centro de la circunferencia el punto
(0, b), ´esta tiene por ecuaci´on x2 + (y − b)2 = r2. El volumen, aplicando el
m´etodo de los discos, vendr´a dado por:
V = π
r
−r
b + r2 − x2
2
− b − r2 − x2
2
dx = (cambio x = r sen t)
= 4bπ
π/2
−π/2
r2
cos2
t dt = 2br2
π t +
1
2
sen 2t
π/2
−π/2
= 2br2
π2
.
PROBLEMA 11.62
Hallar el volumen de un cono recto de altura h, cuya base es una
elipse de eje mayor 2a y eje menor 2b.
Soluci´on
La secci´on determinada en el cono por un plano paralelo a la base y de
altura OP = z es una elipse de eje mayor 2x y eje menor 2y. Su ´area es pues
πxy.
92

57. Por semejanza de tri´angulos, se deduce de la figura que
MPC ∼ MOA =⇒
PC
OA
=
PM
OM
es decir
x
a
=
h − z
h
;
MPD ∼ MOB =⇒
PD
OB
=
PM
OM
es decir
y
b
=
h − z
h
.
El ´area de la secci´on es entonces πxy =
πab(h − z)2
h2
. Luego,
V =
πab
h2
h
0
(h − z)2
dz =
πabh
3
.
PROBLEMA 11.63
Un s´olido tiene una base circular de radio 2. Cada secci´on produ-
cida por un plano perpendicular a un di´ametro fijo es un tri´angulo
equil´atero. Calcular el volumen del s´olido.
Soluci´on
Si expresamos por la ecuaci´on x2 +y2 = 4 a la base del s´olido y consideramos
las secciones perpendiculares al eje X, el lado de un tri´angulo gen´erico es
l = 2y y la altura es h = l2 − l2/4 = l
√
3/2 = y
√
3.
93

58. El volumen ser´a entonces
V =
2
−2
2y · y
√
3
2
dx =
√
3
2
−2
(4 − x2
) dx =
32
√
3
3
.
PROBLEMA 11.64
Un cilindro cuya base es una elipse se corta por un plano inclinado
que pasa por el eje menor de la misma. Hallar el volumen del s´olido
restante.
Soluci´on
Supongamos que la ecuaci´on de la elipse es x2/a2 +y2/b2 = 1 y llamamos H
a la altura del cilindro (que corresponde al punto (a, 0)). Cortando el s´olido
por planos perpendiculares al eje OY obtenemos tri´angulos rect´angulos se-
mejantes. En un punto arbitrario (x, y) el ´area de uno de dichos tri´angulos
(ver figura) es
A =
x · h
2
=
x2 · tg α
2
=
x2 · H
2a
.
94

59. Como (x, y) verifica la ecuaci´on de la elipse, escribimos el ´area en funci´on
de y como A(y) =
a2(1 − y2/b2) · H
2a
. El volumen ser´a entonces
V =
b
−b
A(y) dy = 2
b
0
a(1 − y2/b2) · H
2
dy = aH y −
y3
3b2
b
0
=
2abH
3
.
PROBLEMA 11.65
Un s´olido tiene una base en forma de elipse cuyos ejes mayor y
menor miden 10 y 8 unidades respectivamente. Hallar su volumen
sabiendo que toda secci´on del mismo perpendicular al eje mayor
es un tri´angulo is´osceles de altura igual a 6.
Soluci´on
Escribimos la ecuaci´on de la elipse como x2/25 + y2/16 = 1.
95

60. El tri´angulo obtenido por la secci´on perpendicular al eje OX por un punto
x tiene ´area A(x) = 2y · h/2 = 6y = 24 1 − x2/25, y el volumen del s´olido
(aplicando los m´etodos usuales de integraci´on) es
V =
5
−5
A(x) dx = 24
5
−5
1 − x2/25 dx
=
24
5
25
2
arc sen
x
5
+
x
2
25 − x2
5
−5
= 60π.
PROBLEMA 11.66
La secci´on de un cierto s´olido por cualquier plano perpendicular
al eje OX es un cuadrado tal que los extremos de una diagonal
pertenecen respectivamente a las par´abolas y2 = 4x, x2 = 4y. Hallar
el volumen del s´olido.
Soluci´on
La regi´on que limitan ambas curvas viene indicada en la figura y los puntos
de corte son (0, 0) y (4, 4).
96

61. Como indica el enunciado, la diagonal de un cuadrado gen´erico une los
puntos (x, y1) y (x, y2) y su longitud, en funci´on de x es d = 2
√
x − x2/4.
Como el ´area del cuadrado es A(x) = d2/2 = (2
√
x − x2/4)2/2, el volumen
pedido es:
V =
4
0
(2
√
x − x2/4)2
2
dx =
1
2
2x2
+
x5
80
−
2x7/2
7
4
0
=
144
35
.
C. LONGITUD DE CURVAS PLANAS.
Dada la funci´on y = f(x), definida en un intervalo [a, b], a cada partici´on
P = {x0 = a, x1, . . . , xn−1, xn = b} de [a, b] le corresponde una poligonal de
v´ertices Pk = (xk, f(xk)), k = 0, 1, . . . , n, como indica la figura.
La longitud del arco de la curva entre los puntos A y B de abscisas x = a y
x = b se define como el supremo de los per´ımetros de todas las poligonales. Si
es finito, se dice que la curva es rectificable; si no, la curva no es rectificable
(tiene longitud infinita). El resultado fundamental que aplicaremos en esta
secci´on es el siguiente:
Teorema. Si una funci´on y = f(x) tiene derivada de primer orden continua
en [a, b], entonces es rectificable y la longitud del arco viene dada por la
f´ormula
l = AB =
b
a
1 + [f (x)]2 dx.
97

62. Si la funci´on viene expresada en coordenadas param´etricas x = x(t), y =
y(t), la f´ormula queda de la forma
l =
t1
t0
[x (t)]2 + [y (t)]2 dt,
siendo t0 y t1 los par´ametros correspondientes a los puntos inicial y final de
la curva.
En la mayor´ıa de los casos no es posible encontrar expresiones expl´ıcitas de
la longitud de un arco de curva. Por ello se deben crear nuevas funciones,
como es el caso de las integrales el´ıpticas (que expresan longitudes de arcos de
elipses), o utilizar m´etodos aproximados para calcular arcos de curva.
PROBLEMA 11.67
Hallar la longitud del arco de la par´abola x2 = 2py, con p > 0,
comprendida en el intervalo [0, a].
Soluci´on
Si calculamos la derivada de la funci´on, tenemos
y = x/p =⇒ 1 + y 2 = 1 + (x/p)2 =
x2 + p2
p
.
La longitud del arco pedido queda entonces
l =
1
p
a
0
x2 + p2 dx =
p
2
x x2 + p2
p2
+ ln
x + x2 + p2
p
a
0
=
p
2
a a2 + p2
p2
+ ln
a + a2 + p2
p
.
PROBLEMA 11.68
Probar que la curva f(x) =
x cos(π/x) si x = 0
0 si x = 0
no es rectificable
en [0, 1].
98

63. Soluci´on
Si consideramos los puntos xn = 1/n, con n ∈ N, sabemos que f(xn) =
(−1)n
n
y la longitud de la poligonal de v´ertices xn es
n≥1
ln =
n≥1
1
n
−
1
n + 1
2
+
(−1)n
n
−
(−1)n+1
n + 1
2
=
n≥1
2
n
,
que es una serie divergente. Esto prueba que la curva no es rectificable en
[0, 1].
PROBLEMA 11.69
Calcular la longitud del arco de curva y = ln(cos x) en el intervalo
[0, π/3].
Soluci´on
Como la derivada de la funci´on es y = − tg x, la longitud pedida es
l =
π/3
0
1 + tg2 x dx = ln(sec x + tg x)
π/3
0
= ln(2 +
√
3).
PROBLEMA 11.70
Hallar la longitud de la curva de ecuaci´on 8a2y2 = x2(a2 − 2x2).
Soluci´on
−a/
√
2 a/
√
2
Si escribimos la ecuaci´on en forma expl´ıcita, tenemos y = ±
x
2
√
2a
a2 − 2x2,
de donde y 2
=
(a2 − 4x2)2
8a2(a2 − 2x2)
y 1 + y 2 =
3a2 − 4x2
2
√
2a
√
a2 − 2x2
.
La longitud del arco ser´a:
99

64. L = 4 ·
1
2
√
2a
a/
√
2
0
3a2 − 4x2
√
a2 − 2x2
dx
= 2a · arc sen
x
√
2
a
+
√
2
a
· x · a2 − 2x2
a/
√
2
0
= πa.
PROBLEMA 11.71
Hallar la longitud de la astroide de ecuaci´on x2/3 + y2/3 = a2/3.
Soluci´on
Escribiendo la ecuaci´on en forma param´etrica como x = a cos3 t, y =
a sen3 t y teniendo en cuenta la simetr´ıa de la figura, la longitud viene dada
por:
L = 4
π/2
0
x (t)2 + y (t)2 dt = 4
π/2
0
3a sen t cos t dt = 6a.
PROBLEMA 11.72
Hallar la longitud de un lazo de la cicloide x = a(t − sen t), y =
a(1 − cos t).
Soluci´on
2aπ 4aπ
100

65. Como un lazo de la cicloide es el arco de curva comprendido en el intervalo
t ∈ [0, 2π], la longitud es:
L =
2π
0
x (t)2 + y (t)2 dt =
2π
0
a (1 − cos t)2 + sen2 t dt
= a
√
2
2π
0
√
1 − cos t dt = a
√
2
2π
0
√
2 sen(t/2) dt = 8a.
PROBLEMA 11.73
Hallar la longitud de la curva cuya ecuaci´on en forma param´etrica
es x(t) = a cos3 t, y(t) = a sen t(1 + cos2 t).
Soluci´on
Debido a la simetr´ıa de la figura, por la f´ormula de la longitud de arco
tenemos:
L = 4
π/2
0
x (t)2 + y (t)2 dt = 4
π/2
0
a cos t 4 − 3 sen2 t dt = (cambio
√
3
2
sen t = sen u) =
16a
√
3
π/3
0
cos2
u du =
8a
√
3
u +
sen 2u
2
π/3
0
=
2a(4π + 3
√
3)
3
√
3
.
101

66. D. EJERCICIOS PROPUESTOS.
1. Encontrar una f´ormula que permita calcular el ´area de cada una
de las regiones I, II, III y IV de la figura siguiente:
Resp.: Si llamamos r(x) = f(0) +
g(b) − f(0)
b
· x a la recta que pasa
por los puntos (0, f(0)) y (b, g(b)), tenemos:
AI =
b
a
[f(x) − g(x)] dx;
AII =
a
0
[h(x) − g(x)] dx +
b
a
[h(x) − f(x)] dx;
AIII =
a
0
[f(x) − r(x)] dx +
b
a
[g(x) − r(x)] dx;
AIV =
a
0
[g(x) − f(x)] dx.
2. Hallar el ´area de la figura limitada por la hip´erbola equil´atera
xy = a2, el eje OX y las rectas x = a, x = 2a.
Resp.: A = a2 ln 2.
3. Hallar el ´area encerrada por la recta y = 1 y la curva y = ln2
x.
Resp.: A = 4/e.
4. Calcular el ´area limitada por las curvas y = (x−4)2, y = 16−x2.
102

67. Resp.: A = 64/3.
5. Hallar el ´area limitada por la curva y = x2 − 2x + 2, su tangente
en el punto (3, 5), el eje OX y el eje OY .
Resp.: A = 23/8.
6. Calcular el ´area de la figura del primer cuadrante limitada por las
par´abolas x2 = 2py, y2 = 2px en el interior de la circunferencia
x2 + y2 = 3p2, (p > 0).
Resp.: A =
p2
24
(4
√
2 + 9π − 36 arc sen 1/
√
3).
7. Calcular el ´area de la regi´on limitada por las curvas y = −x2 + 6,
(y − 2)2 + x2 = 4, y = x.
Resp.: A =
1
6
(49 − 6π).
8. Hallar el ´area de la regi´on limitada por la curva y = (x2 + 2x)e−x
y el eje OX en el tercer cuadrante.
Resp.: A = 4.
9. Hallar el ´area de la regi´on limitada por la curva y =
x
(1 − x2)2
· arc sen x
y las rectas x = 0, x = 1/2, y = 0.
Resp.: A =
π
9
−
1
2
√
3
.
10. Calcular el ´area de la regi´on limitada por las curvas y = 5 − x2,
y = (x − 1)2.
Resp.: A = 9.
11. Calcular el ´area de la elipse
x2
a2
+
y2
b2
= 1.
Resp.: A = πab.
12. Calcular el ´area de la regi´on limitada por las curvas x2 + y2 = 2,
y = x2, y = x + 6.
Resp.: A =
45 + π
2
.
103

68. 13. Calcular el ´area de la regi´on limitada por las gr´aficas de f(x) =
x2 − 4x + 4 y g(x) = 4 − x.
Resp.: A = 9/2.
14. Calcular el ´area de la figura limitada por la curva y = x3, la recta
y = 8 y el eje OY .
Resp.: A = 12.
15. Hallar el ´area limitada por la curva y2 = x2 − x4.
Resp.: A = 4/3.
16. Hallar el ´area de la superficie interior a la circunferencia x2 +
y2 = 16 y por encima de la par´abola x2 = 12(y − 1).
Resp.: A =
16π + 4
√
3
3
.
17. Hallar el ´area limitada por la curva y = cos 2x + cos x y el eje X
entre las dos ordenadas que corresponden a una distancia igual
a un per´ıodo de la curva.
Resp.: A = 3
√
3.
18. Hallar el ´area encerrada por el bucle de la curva x3 = a(x2 −y2).
Resp.: A =
8a2
15
.
19. Dada la hip´erbola de ecuaci´on
x2
a2
−
y2
b2
= 1, determinar el ´area A
del tri´angulo mixtil´ıneo APQ, siendo A(a, 0), P(a
√
2, b), Q(a
√
2, 0).
Resp.: A =
ab
2
[
√
2 − ln(1 +
√
2)].
20. Hallar el ´area del segmento circular de centro O y radio r com-
prendido entre las rectas x = a, x = b.
Resp.: A = b r2 − b2 + r2
arc sen
b
r
− a r2 − a2 − r2
arc sen
a
r
.
104

69. 21. Hallar el ´area del segmento parab´olico comprendido entre y2 =
2px las rectas x = a, x = b.
Resp.: A =
4
√
2p
3
(b3/2
− a3/2
).
22. Hallar el volumen del s´olido de revoluci´on engendrado por la
figura limitada por la curva y = xex y las rectas y = 0, x = 1 al
girar alrededor del eje OX.
Resp.: V =
πe2
4
.
23. Calcular el volumen del s´olido engendrado al girar alrededor del
eje OX la regi´on interior a la circunferencia x2 + y2 = 1 y a la
par´abola y2 = 3x/2.
Resp.: 19π/48.
24. Calcular el volumen del s´olido obtenido al girar alrededor del eje
OX la regi´on limitada por la curva y = 2 −
√
1 − x2 y el eje OX.
Resp.: V =
π
3
(28 − 6π).
25. Calcular el volumen del s´olido limitado por las curvas x2 −y2 = 4,
y = 2, y = −2 al girar alrededor del eje OX.
Resp.: V =
32π
3
(2
√
2 − 1).
26. Calcular el volumen del s´olido limitado por las curvas y = sen x,
y = 2x/π al girar alrededor del eje OX.
Resp.: V = π2/6.
27. Calcular el volumen del s´olido obtenido al girar la regi´on limitada
por las gr´aficas de f(x) =
√
4 − x2 y g(x) = 1 en el intervalo [0,
√
3]
alrededor de y = 0.
Resp.: V = 2π
√
3.
28. Sea R la regi´on interior a la circunferencia de centro (1, −1) y
radio 2 y por encima de la recta y =
√
3 − 1.
a) Determinar el ´area de R.
105

70. b) Calcular el volumen del s´olido obtenido al girar la regi´on R
alrededor del eje OX.
Resp.: A =
2π
3
−
√
3; V =
2π
3
(2 + 3
√
3 − 2π).
29. Sea R la regi´on limitada por las curvas x + y = 2y2, y = x3. Cal-
cular el ´area de R y el volumen que engendra R al girar alrededor
del eje OX.
Resp.: A = 7/12 (pensar x como funci´on de y); V = 11π/21 (m´etodo
de los tubos).
30. Sea R la regi´on limitada por las curvas y =
x2
4
+ 2 y 5x+8y−14 =
0. Calcular el ´area de R y el volumen de la figura obtenida al girar
R alrededor del eje OX.
Resp.: A = 27/192; V =
891π
1280
(m´etodo de los discos).
31. Sea R la regi´on limitada por las curvas y = 4x − x2 y 2x − y = 0.
Calcular el ´area de R y el volumen de la figura obtenida al girar
R alrededor del eje OX.
Resp.: A = 4/3; V = 32π/5.
32. Sea R la regi´on limitada por las curvas y =
1
1 + x2
e y =
x2
2
. Cal-
cular el ´area de R y el volumen de la figura obtenida al girar R
alrededor de los ejes OX y OY .
Resp.: A = (3π − 2)/6; VX =
π
20
(5π + 8) (discos); VY =
π
4
(4 ln 2 − 1)
(tubos).
33. Se considera la regi´on R limitada por las curvas x2 +(y −1)2 = 5,
x = 2(y − 1)2.
a) Calcular el ´area de R.
b) Calcular el volumen obtenido al girar la regi´on R alrededor
del eje OY .
c) Calcular el volumen obtenido al girar la regi´on R alrededor de
la recta y = 1.
106

71. Resp.: A = 5 arc sen
1
√
5
+
2
3
; VY =
116π
15
(discos); Vy=1 =
10
√
5 − 19
3
· π
(tubos).
34. Dada la regi´on limitada por las curvas y = 4x2, y = x2/9, y = 2,
calcular el ´area de la regi´on y el volumen obtenido al girar dicha
regi´on alrededor de los ejes OX y OY .
Resp.: A = 20
√
2/3; VX = 16π
√
2 (tubos); VY = 35π/2 (discos).
35. Dada la regi´on limitada por las curvas y = x2 + 1, y − 1 = x,
calcular el ´area de la regi´on y el volumen obtenido al girar dicha
regi´on alrededor del eje OY .
Resp.: A = 1/6; VY = π/6.
36. Dada la regi´on limitada por las curvas x2 + y2 = 12, x2 = 4y,
y2 = 4x, calcular el ´area de la regi´on y el volumen obtenido al
girar dicha regi´on alrededor del eje OY .
Resp.: A =
4
√
2
3
+ 12 arc sen 2/3 − 3π; VY =
π
15
(256
√
5 − 200).
37. Se considera la regi´on limitada por la curva y = sen(πx/2) +
cos(πx/2) + 1 y las rectas x = 0, x = 1 e y = 0. Hallar el ´area de
dicha regi´on y el volumen del s´olido obtenido al girar alrededor
del eje OX.
Resp.: A = 1 +
4
π
; V = 2π + 10.
38. Calcular el volumen del tronco de cono con radios de las bases r
y R y altura h.
Resp.: V =
πh
3
(r2
+ rR + R2
).
39. Calcular la longitud del arco de la curva y = ex/2 + e−x/2 entre
los puntos de abscisa x = 0 y x = 2.
Resp.: L = e − e−1
.
40. Calcular la longitud del arco de la curva y = ln
ex + 1
ex − 1
entre x = 1
y x = 2.
Resp.: L = ln(e2 + 1) − 1.
107