Este documento presenta varios ejercicios de resistencia de diseño para miembros en tensión. Cada ejercicio describe la geometría del miembro, el material y las conexiones, y guía los cálculos para determinar la resistencia de diseño considerando la sección gruesa y la sección neta. Los valores calculados se comparan para determinar el valor de diseño que gobierna.









































![Solución
a.- La carga de 20kips no puede moverse de la posición mostrada
De acuerdo al grafico se tiene
la carga muerta = peso de la viga = 0.0048kips/ft
ftkipswww LDu /0576.0)048.0(2.16.12.1 ==+=
kipsPPP LDu 0.32)20(6.16.12.1 ==+=
Por la simetría de la barra y la condición del problema se puede deducir la tensión de las
cuerdas:
[ ] kipsTu 86.1632)30(00576.0
2
1
=+=
El área requerida
2
5168.0
)58)(75.0(75.0
86.16
)75.0(75.0
in
F
T
A
u
u
b ===
Igualando el área tenemos:
despejando
d
Ab ,
4
2
π
= ind 811.0
)5168.0(4
==
π
Requerimiento indind
8
7,811.0 ==](https://image.slidesharecdn.com/problemasresueltosdeaceroymadera-140804165734-phpapp01/85/Problemas-resueltos-de-acero-y-madera-43-320.jpg)
![b.- La carga de 20kips puede estar situada en cualquier lugar entre las dos barras.
La máxima fuerza en requerido en la viga es cuando la carga viva esta en A y D entonces
se tiene:
[ ] kipsTu 86.3232)30(00576.0
2
1
=+=
Entonce el área requerida se tendrá:
2
007.1
)58)(75.0(75.0
86.32
)75.0(75.0
in
F
T
A
u
u
b ===
,007.1
4
2
=
dπ
Despejando d se tiene ind 13.1=
Requerimiento indind 4
11,13.1 ==
3.7.3 Como se muestra en la figura el miembro AC se usa para contraventear la
estructura articulada contra cargas horizontales. Seleccione una barra roscada de acero
A36. La carga de 10kips esta factorizada.
Solución
La condición del problema nos dice la fuerza de 10k está factorada por lo tanto de
acuerdo a las ecuaciones combinadas de LRFD tenemos:
kipsw 16)10(6.16.1 ==
En el puntos B En el punto C
16k O 16k 16k O](https://image.slidesharecdn.com/problemasresueltosdeaceroymadera-140804165734-phpapp01/85/Problemas-resueltos-de-acero-y-madera-44-320.jpg)

![[ ] 0)15()96.30()15(56 =°−=∑ TsenMc Despejando T se tiene kipsT 9.108=
El área requerida seria:
2
338.3
)58)(75.0(75.0
9.108
)75.0(75.0
in
F
T
A
u
u
b ===
Despejando d en la siguiente ecuación 338.3
4
2
=
dπ
despejando se tiene ind 062.2=
Requerimiento indind 8
12,06.2 ==
3.7.5.- Un tubo esta soportado a intervalos de 10pies por medio de una barra doblada
roscada como se muestra en la figura. Si se usa un tubo de acero de 10in de diámetro
lleno de agua Que tamaño de barra se requiere Considere Acero A36.
Solución
El diámetro del tubo es ind 0.10=
El volumen de agua por longitud de pie es = 3
22
5.94212
4
)0.10(
12
4
inxx
d
==
ππ
El peso total por pie es:
El peso del agua + el peso del tubo= ( ) ftlb /53.745.40)4.62
)12(
5.942
3
=+](https://image.slidesharecdn.com/problemasresueltosdeaceroymadera-140804165734-phpapp01/85/Problemas-resueltos-de-acero-y-madera-46-320.jpg)








![Cubierta de techo = 6psf
wu:= [1.2(0.472 + 6) + 1.6⋅26.833]psfwu= 50.7 psf
Componente de las cargas paralela a la superficie del techo = 1/(5)e1/2⋅wu = 22.67 psf
Cargas sobre el tensor inclinado superior = 1/12(44.47ft2)(7) w( u) = 14.467 klb
AD = Pu/(0.75⋅0.75⋅Fu) AD = 1.05 in2
Use tensores de 5/8 pulg con 11 cuerdas por pulgada.](https://image.slidesharecdn.com/problemasresueltosdeaceroymadera-140804165734-phpapp01/85/Problemas-resueltos-de-acero-y-madera-55-320.jpg)



![Solución
Ag := L1⋅e + (L2 − e) ⋅e Ag = 6.434 in2
Aorificio:= 2e⋅(huelgo+ φperno) Aorificio= 1.125 in2
Aneta:= Ag − AorificioAneta = 5.309 in2Respuesta
SOLUCIONARIO DE EJERCICIOS DE DISEÑO ACERO Y MADERA
PROBLEMA 3-2-1
Para la obtención de la sección bruta,
Ag = 7 (3/8) = 2. 625 cm2,
P "= FyAs = 36 (2.625) = 94. 5 kips
Para la fractura de la sección neta,
Ag = (3/8) [7- (1 + 1/8)] = 2. 203 cm2
Pn= FuAe = 58 (2,203) = 127. 8 kips
a) La resistencia de diseño en base a
øtPn = 0.90 (94.5) = 85. 05kips
La resistencia de diseño sobre la base de la fractura es
øtPn=0.75 (127,8) = 95. 85 kips
La resistencia de diseño para LRFD es el menor valor: øtPn = 85.1kips
b) La resistencia admisible sobre la base de obtención es:
La resistencia admisible sobre la base de fractura es:](https://image.slidesharecdn.com/problemasresueltosdeaceroymadera-140804165734-phpapp01/85/Problemas-resueltos-de-acero-y-madera-60-320.jpg)

















































































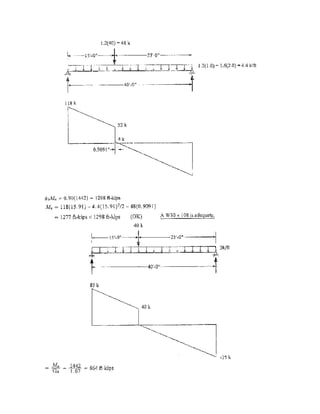


























































![Solucion
a.- La carga de 20kips no puede moverse de la posición mostrada
De acuerdo al grafico se tiene
la carga muerta = peso de la viga = 0.0048kips/ft
ftkipswww LDu /0576.0)048.0(2.16.12.1 ==+=
kipsPPP LDu 0.32)20(6.16.12.1 ==+=
Por la simetría de la barra y la condición del problema se puede deducir la
tensión de las cuerdas:
[ ] kipsTu 86.1632)30(00576.0
2
1
=+=
El área requerida
2
5168.0
)58)(75.0(75.0
86.16
)75.0(75.0
in
F
T
A
u
u
b ===
Igualando el área tenemos:
despejando
d
Ab ,
4
2
π
= ind 811.0
)5168.0(4
==
π](https://image.slidesharecdn.com/problemasresueltosdeaceroymadera-140804165734-phpapp01/85/Problemas-resueltos-de-acero-y-madera-204-320.jpg)
![Requerimiento indind
8
7,811.0 ==
b.- La carga de 20kips puede estar situada en cualquier lugar entre las dos barras.
La máxima fuerza en requerido en la viga es cuando la carga viva esta en A y D
entonces se tiene:
[ ] kipsTu 86.3232)30(00576.0
2
1
=+=
Entonce el área requerida se tendrá:
2
007.1
)58)(75.0(75.0
86.32
)75.0(75.0
in
F
T
A
u
u
b ===
,007.1
4
2
=
dπ
despejando d se tiene ind 13.1=
Requerimiento indind 4
11,13.1 ==
3.7.3.- Como se muestra en la figura el miembro AC se usa para contraventear la
estructura articulada contra cargas horizontales. Seleccione una barra roscada
de acero A36. La carga de 10kips esta factorizada.
Solución](https://image.slidesharecdn.com/problemasresueltosdeaceroymadera-140804165734-phpapp01/85/Problemas-resueltos-de-acero-y-madera-205-320.jpg)

![Solución
Realizando las combinaciones del diseño de LRFD
kipsLDPu 56)35(6.16.12.1 ==+=
[ ] 0)15()96.30()15(56 =°−=∑ TsenMc Despejando T se tiene kipsT 9.108=
El área requerida seria:
2
338.3
)58)(75.0(75.0
9.108
)75.0(75.0
in
F
T
A
u
u
b ===
Despejando d en la siguiente ecuación 338.3
4
2
=
dπ
despejando se tiene
ind 062.2=
Requerimiento indind 8
12,06.2 ==](https://image.slidesharecdn.com/problemasresueltosdeaceroymadera-140804165734-phpapp01/85/Problemas-resueltos-de-acero-y-madera-207-320.jpg)


