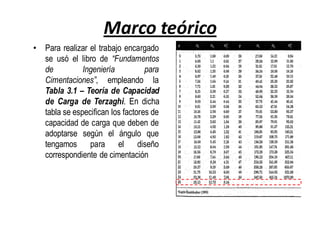
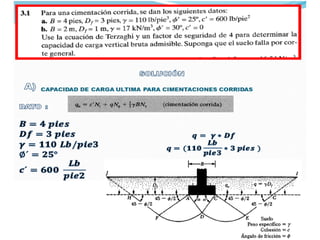
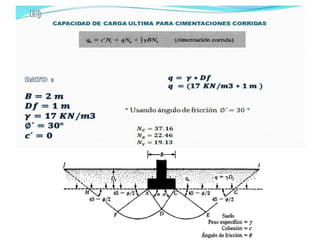
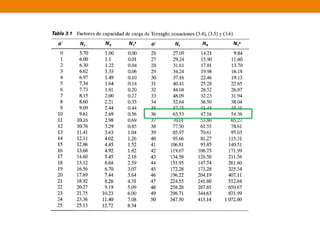
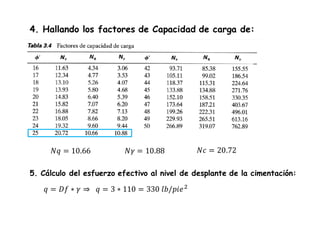
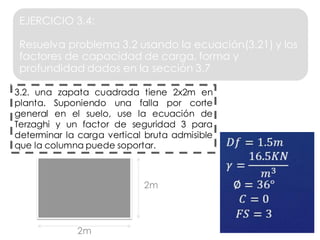
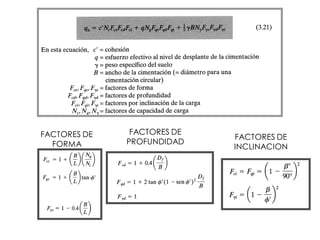
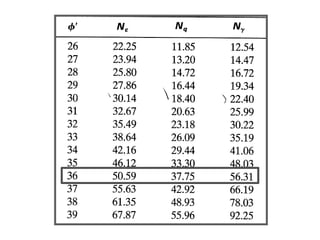
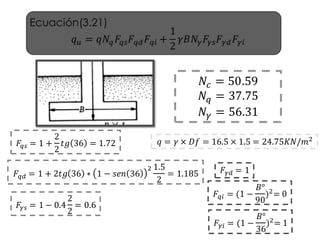
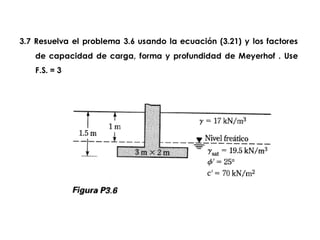
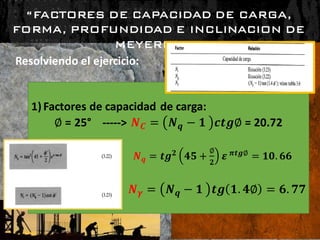
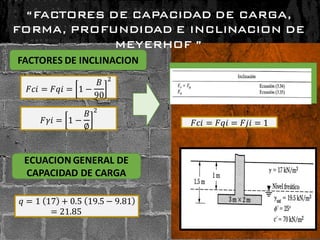
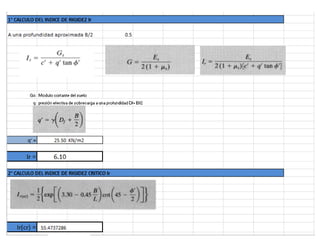
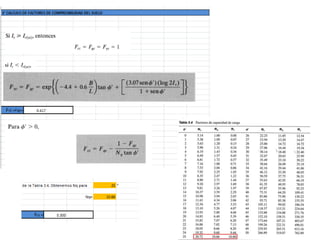
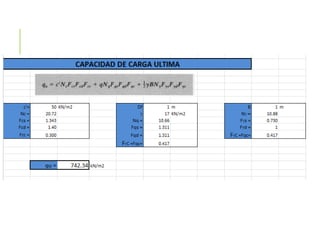
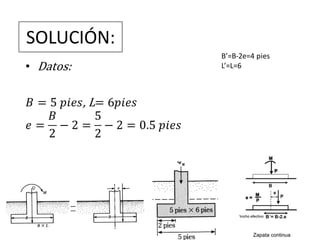
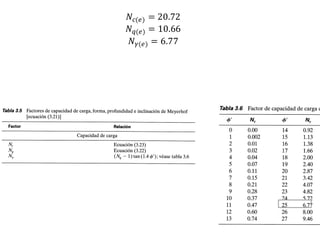
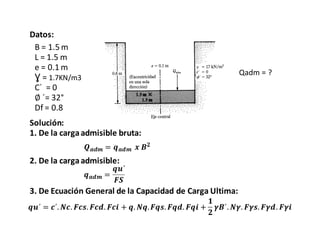
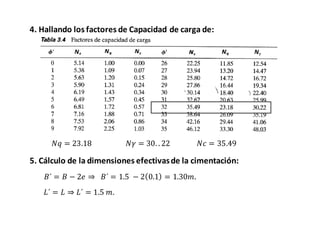
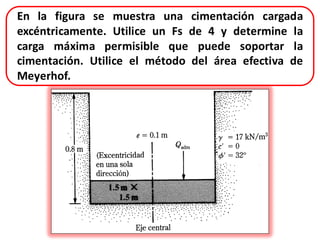
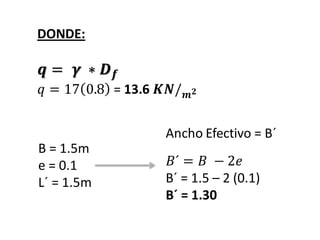
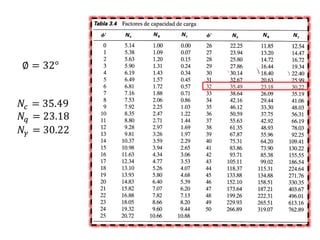
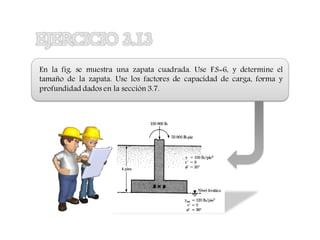
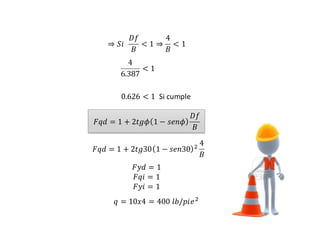
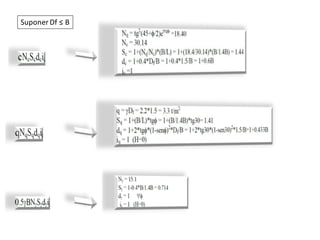
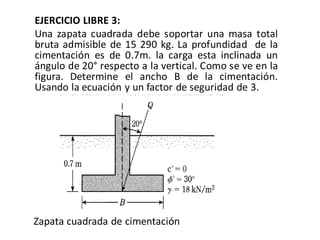
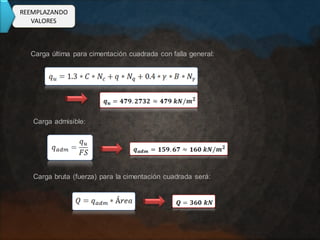
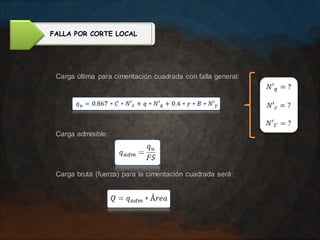
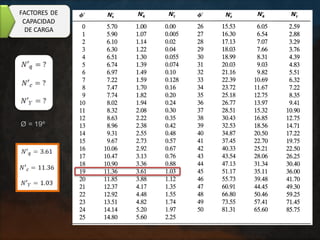
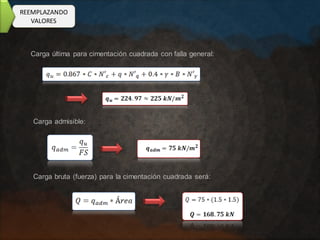
El documento presenta varios ejercicios de diseño de cimientos. El Ejercicio 1 describe el marco teórico utilizando la Tabla 3.1 de Terzaghi para determinar factores de capacidad de carga. El Ejercicio 2 resuelve un problema de diseño de zapata usando la ecuación general de Terzaghi. El Ejercicio 3 resuelve dos problemas de diseño de cimientos corridos usando la ecuación general y factores.