Este documento presenta varios problemas resueltos sobre flexión y deformaciones en vigas. En el primer problema, se calcula la ecuación de la línea elástica, los giros en las secciones extremas y la flecha máxima de una viga IPE-160 sometida a una carga concentrada usando el método de la ecuación diferencial de la línea elástica. En el segundo problema, se determinan los mismos parámetros usando los teoremas de Mohr. Los problemas posteriores involucran el cálculo de giros, flechas y dimensionamiento

1. Tema 6: FLEXIÓN: DEFORMACIONES
x
+
y
Problemas resueltos
Prof.: Jaime Santo Domingo Santillana
E.P.S.-Zamora – (U.SAL.) - 2008

2. 6.1.-La viga de la figura es una IPE-160 y está sometida a la carga concentrada indicada
de 30 kN. Calcular por el Método de la Ecuación Diferencial de la Línea Elástica:
1) Ecuación de la Línea Elástica
2) Giros de las secciones extremas A y B
3) Flecha máxima
Datos: E= 2,1x105 N/mm2
RA RB
30 kN
A B
1m 3m
Cálculo de reacciones: Ecuaciones de equilibrio
∑F =0 RA + RB = 30
→
RA = 22,5 kN
∑M = 0 RB .4 = 30.1 RB = 7,5 kN
A
1) Ecuación de la línea elástica: (fórmula general de la ecuación diferencial de la línea
d2y M
elástica): 2
=− z
dx E .I z
0 − x −1 1− x − 4
M z = 22,5.x M z = 22,5.x − 30.( x − 1) = −7,5 x + 30
d2y d2y
E .I z . = −22, 5.x E.I z . = 7,5.x − 30
dx 2 dx 2
dy x2 dy x2
E .I z . = −22,5. + C1 E.I z . = 7,5. − 30.x + C3
dx 2 dx 2
3 3
x x x2
E .I z . y = −22, 5. + C1 .x + C2 E.I z . y = 7,5. − 30. + C3 .x + C4
6 6 2
Cálculo de las constantes → condiciones de contorno:
x = 0 → y0 −1 = 0 x = 1 → y0 −1 = y1− 4
dy  dy 
x =1→  =  x = 4 → y1− 4 = 0 y operando se obtiene :
dx 0 −1 dx 1− 4
C1 = 26, 25 C2 = 0 C3 = 41, 25 C 4 = −5 y sustituyendo estos valores :
0 − x −1 1− x − 4
. ( 3, 75.x 2 − 30.x + C3 )
dy 1
. ( −11, 25.x 2 + 26, 25 )
dy 1 =
=
dx E .I z dx E.I z
. (1, 25.x 3 − 15.x + 41, 25.x − 5 )
1
. ( −3, 75.x 3 + 26, 25.x )
1 y=
y=
E .I z E .I z

3. 2) Giros de las secciones A y B:
dy  26, 25
ϑA =  ( para x = 0 ) = = 0, 014 rad
dx  0−1 2.1.10 .103.869.10 −8
5
siendo: E = 2.1.10 6 Kg / cm 2 I z ( IPE − 160) = 869 cm 4
dy  3, 75.4 2 − 30.4 + 41, 25
ϑB =  ( para x = 4 ) = = −0, 01 rad
dx 1− 4 2,1.105.103.869.10 −8
3) Flecha máxima
dy
0 − x − 1: ymax → = 0 → 0 = −11, 25.x 2 + 26, 25 → x = ±1, 53 m ( fuera del tramo)
dx
dy
1 − x − 4 : ymax → = 0 → 0 = 3, 75.x 2 − 30.x + 41, 25 → x = 6, 24 m ( fuera del tramo)
dx
x = 1, 76 m
1, 25.1, 763 − 15.1, 762 + 41, 25.1, 76 − 5
ymax = y1− 4 ( x = 1, 76 m) = = 0, 015 m = 1,5 cm ↓
2,1.105.103.869.10−8

4. 6.2.-En la viga de la figura se pide determinar por el Método de los Teoremas de Mohr:
1) Giros de las secciones A y B
2) Flecha máxima
Datos: E= 2,1x105 N/mm2, Iz= 2770 cm4
30 kN 30 kN
RB
RA
1m A 3m B 1m
Cálculo de las reacciones: por simetría de cargas y de estructura:
30 + 30
R A = RB = = 30 kN
2
30 kN 30 kN
θA θB
C tag en C
δAC yC
δOC yO A B
x
30 kN 30 kN
O
1m 1,5 m 1,5 m 1m
y
30
-
x
O
A C B
Mz
por simetría de estructura y de c arg as → ϑC = 0 → tagϑC = 0 (horizontal )
S M AC −30.1, 5
ϑAC = ϑA − ϑC = ( como ϑC = 0 ) = ϑA = = = −0, 0077 rad
E.I z 2,1.10 .103.2770.10 −8
5
S M CB −30.1,5
ϑCB = ϑC − ϑB = (como ϑC = 0) = −ϑB = = = −0, 0077 rad
E.I z 2,1.10 .103.2770.10−8
5
así pues:
ϑ A = −0,0077 rad ϑB = 0,0077 rad

5. M
QA AC −30.1,5.0, 75
δ AC = = = −0, 0058 m = −0,58 cm
E.I z 2,1.108.2770.10−8
(δ AC < 0 → A está por debajo de la tan gente en C )
yC = δ AC = 0,58 cm → yC = −0,58 cm ↑
yO = δ OC − yC
1 2
M OC (− .1.30. .1) + (−30.1,5.1, 75)
Q
δ OC = O
= 2 3 = −0, 01526 m = −1,526 cm
E.I z 2,1.108.2770.10−8
(δ OC < 0 → O está por debajo de la tan gente en C )
yO = δ OC − yC = 1,526 − 0,58 = 0,946 cm → y0 = 0,946 cm ↓
y MAX = yO = 0,946 cm ↓

6. 6.3.-La viga de la figura es una IPE-160. Calcular por el Método de los Teoremas de
Mhor:
1) Giros de las secciones A y B
2) Flecha en C
3) Flecha máxima
Dato: E= 2,1x105 N/mm2
RB 30 kN
RA
A B C
3m 1m
Cálculo de reacciones: Ecuaciones de equilibrio:
∑F =0 RB = 30 + RA
→
RA = 10 kN
∑M = 0 A RB .3 = 30.4 RB = 40 kN
30
-
hD
x
xD
Mz tag en A
θB hC
δBA δCA
D tag en D
δAD θA yD B
A
yC
C
1) Giros en A y B:
1 1
M .3.(−30). .3
QB AB
δ BA = = 2 3 = −0, 02466 m ( punto B por debajo tan gente en A)
E.I z 2,1.108.869.10−8
δ BA 0, 02466
δ BA = ϑA .3 → ϑA = = = 0, 0082 rad ( sentido antihorario, ver figura)
3 3
1
.3. ( −30 )
S M AB
ϑAB = ϑA − ϑB = − 0, 082 − ϑB = 2 → ϑB = 0, 0165 rad
E.I z 2,1.108.869.10−8
ϑ A = −0,0082 rad ϑB = 0,0165 rad

7. 2) Flecha en C:
1 1 1 2
M .3.( −30).(1 + .3) + .1.(−30).( .1)
QC AC 2 3 2 3 = −0, 0548 m
δ CA = = 8 −8
E .I z 2,1.10 .869.10
δ CA < 0 → C está por debajo de la tan gente en A
y C = δ CA − hC = 0,0548 − 0,0328 = 0,022 m = 2,2 cm
siendo : hC = ϑ A .4 = 0,0082.4 = 0,0328 m
y C = 2,2 cm ↓
3) Flecha máxima:
tramo AB : yMAX = y D siendo D un punto en el que : ϑD = 0 (ver figura )
localicemos ese punto D :
S M AD
ϑAD = ϑ A − ϑD = (como ϑD = 0) = ϑA = y sustituyendo valores :
E.I z
1 1
− .xD .hD − .xD .10.xD
−0, 0082 = 2 = 2 → xD = ±1, 73 m
−8
8
2,1.10 .869.10 2,1.108.869.10 −8
30 hD
( por semejanza de tríangulos, ver figura : = → hD = 10.xD )
3 xD
1 2
− .1, 73.10.1, 73. .1, 73
Q M AD 2 3
δ AD = A = = −0, 0095 m = −0,95 cm
E .I z 2,1.10 .869.10−8
8
δ AD < 0 → A está por debajo de la tan gente en D
ymax = y D = y ( x = 1, 73 m = δ AD = 0,95 cm → y D = −0,95 cm ↑
Luego comparando valores, la flecha máxima en toda la viga será:
yC = 2,2 cm ↓

8. 6.4.-En la viga de la figura se pide:
1) Dimensionamiento de la sección a resistencia, empleando criterio plástico
2) Dimensionamiento a rigidez, empleando la condición: ymax ≤ L/200
3) Giros de las secciones C y B (Calcularlos por los dos Métodos estudiados)
4) Flechas en C y B (Calcularlas por los dos Métodos estudiados)
Datos: IPE, fy= 275 N/mm2; γM=1,1; γ =1,35; E= 2,1x105 N/mm2
RA MA 5 kN
2,5 kN
2 kNm
A C B
1m 1m
Cálculo de reacciones: Ecuaciones de equilibrio:
∑F =0 RA = 2,5 + 5 + 2.2 = 11, 5 kN
∑M = 0 A M A = 2,5.1 + 5.2 + 2.2.1 = 16,5 kN .m
1) Dimensionamiento de la sección a resistencia: tracemos los diagramas de esfuerzos:
x
+ 7 5
11,5 9,5
Vy
16,5
6
-
x
Mz
0 − x −1
V y = 11,5 − 2.x x = 0 → V y = 11,5 x = 1 → V y = 9, 5
x
M z = 11, 5.x − 16,5 − 2.x. = −1.x 2 + 11,5.x − 16,5
2
x = 0 → M z = −16, 5 x = 1 → M z = −6
1− x − 2
V y = 11,5 − 2.x − 2, 5 x = 1 → Vy = 7 x = 2 → Vy = 5
x
M z = 11, 5.x − 2.x. − 2,5.( x − 1) = −1.x 2 + 9.x − 14
2
x = 1 → M z = −6 x = 2 → M z = 0

9. Dimensionamiento con criterio plástico:
M z max = 16,5 kN .m
M z* ≤ M zpl ,d = Wzpl . f yd
275
sustituyendo valores :16, 5.106.1,35 ≤ Wzpl . → Wzpl ≥ 89,1.103 mm3
1,1
entrando en tablas IPE → IPE − 160
comprobación a cor tan te V y :
Vy max = 11,5 kN
f yd
Vy* ≤ Vypl ,d = Av .
3
siendo : Av = (area del alma ) = h.t w = ( IPE − 160) = 160.5 = 800 mm 2
275
1,1
sustituyendo valores :11,5.10 .1, 35 ≤ 800.
3
y operando :15,53.103 ≤ 115, 47.103
3
¡ sí cumple a cor tan te ! y además : Vy = 15,53.103 < 0,5.Vypl = 0,5.115, 47.103 = 57, 735.103
*
¡no es necesario combinar momento flector con fuerza cor tan te
2) Dimensionamiento a rigidez: y MAX ≤ L / 200
A tag en A
x
yB = δBA
y
B
M
QB AB
yMAX = y B = δ BA =
E .I z
1 2
∫ (−1.x + 11, 5.x − 16, 5).dx.(2 − x) + ∫ (−1.x + 9.x − 14).dx.(2 − x)
2 2
δ BA = 0 1
2,1.10 .10 .I z .10−8
5 3
−19, 417 19, 417 L 2
δ BA = yMAX = ≤ = → I z ≥ 924, 6 cm 4 → IPE − 180
2,1.I z 2,1.I z 200 200
Así pues para que se cumpla con los dos dimensionamientos: → IPE-180

10. 3) y 4) Giros y Flechas en C y B:
A.- Método de la Ecuación diferencial de la línea elástica:
0 − x − 1 M z = −1.x 2 + 11, 5.x − 16, 5
d2y
E .I z . 2
= − M z = 1.x 2 − 11, 5.x + 16, 5
dx
dy x3 x2
E .I z . = 1. − 11, 5. + 16, 5.x + C1
dx 3 2
4 3
x x x2
E .I z . y = 1. − 11, 5. + 16, 5. + C1 . x + C2
12 6 2
1− x − 2 M z = −1. x 2 + 9. x − 14
d2y
E .I z . = − M z = 1.x 2 − 9.x + 14
dx 2
dy x3 x2
E .I z . = 1. − 9. + 14. x + C3
dx 3 2
4 3
x x x2
E .I z . y = 1. − 9. + 14. + C3 . x + C4
12 6 2
Condiciones de contorno:
dy 
x = 0 → y0 −1 = 0 x=0→  =0
dx  0 −1
dy  dy  C1 = 0 C2 = 0
x = 1 → y0 −1 = y1− 2 x =1→  =  →
dx  0 −1 dx 1− 2 C3 = 1, 25 C4 = −0, 417
sustituyendo las constantes en las ecuaciones anteriores:
0 − x −1 1− x − 2
1 3 11, 5 2 1 3 9 2
.x − .x + 16, 5.x .x − .x + 14.x + 1, 25
dy 3 dy 3 2
= 2 =
dx 2,1.105.103.1320.10 −8 dx 2,1.105.103.1320.10 −8
1 4 11,5 3 16, 5 2 1 4 9 3 14 2
.x − .x + .x .x − .x + .x + 1, 25.x − 0, 417
y= 12 6 2
y = 12 6 2
2,1.105.103.1320.10 −8 2,1.10 .103.1320.10 −8
5
dy  dy 
ϑC =  para x = 1 → 0,00399 rad ϑB =  para x = 2 → 0,00502 rad
dx  0−1 dx 1− 2
yC = y0−1 para x = 1 → 0,00231 m y B = y1− 2 para x = 2 → 0,007 m
ϑC = 0,00399 rad ϑ B = 0,00502rad

11. y C = 0,231 cm ↓ y B = 0,7 cm ↓
B.- Método de los Teoremas de Mohr:
RA MA θC 5 kN
2,50 kN
2 kN/m θB
tag en A
A x
Cy =δ
C CA
yB = δBA
1m 1m B
16,5
6
-
x
A B C
Mz
yB = δBA
S M AC
ϑAC = ϑ A − ϑC = (como ϑA = 0) = −ϑC =
E .I z
1
∫ (−1.x + 11,5.x − 16,5).dx
2
ϑC = − 0 = 0, 00399 rad
2,1.108.1320.10−8
S M AB
ϑAB = ϑ A − ϑB = (como ϑA = 0) = −ϑB =
E .I z
1 2
∫ (−1.x + 11,5.x − 16,5).dx + ∫ (−1.x + 9.x − 14).dx
2 2
ϑB = − 0 1
= 0, 00502 rad
2,1.10 .1320.10−8
8
M
QC AC
yC = δ CA =
E .I z
1
∫ (−1.x + 11,5.x − 16,5).dx.(1 − x)
2
δ CA = 0
= −0, 00231 m → yC = 0, 00231 m
2,1.108.1320.10 −8
(δ CA < 0 → el punto C está por debajo de la tan gente en A)
M
QB AB
y B = δ BA =
E.I z
1 2
∫ (−1x + 11,5 x − 16,5).dx.(2 − x) + ∫ ( −1x 2 + 9 x − 14).dx.(2 − x )
2
δ BA = 0 1
= −0, 007 m
2,1.108.1320.10 −8
(δ BA < 0 → el punto B está por debajo de la tan gente en A) → y B = 0, 007 m
ϑC = 0,00399 rad ϑ B = 0,00502 rad
y C = 0,231 cm y B = 0,7 cm

12. 6.6.-En la viga de la figura de sección rectangular de 30 cm x 40 cm se pide calcular la
flecha en la sección C
Datos: E= 2,1x104 N/mm2
SECCION
60 kN
60 kN
A B 40 cm z
C
3m 2m
y
30 cm
Descompongamos la fuerza de 6000 Kg en la dirección de los ejes principales y,z:
20
tag α = → α = 53,13º
15
Fy = F .senα = 60.sen53,13º = 48 Kg
Fz = F .cos α = 60.cos 53,13º = 36 Kg
60 kN
48 kN
RAy 48 kN RBy
RAz z
RBz
40 cm α 36 kN
A 36 kN C B z
3m 2m
y
y 30 cm
Cálculo de las reacciones: Ecuaciones de equilibrio:
∑F =0 y RAy + RBy = 48 ∑F z =0 RAz + RBz = 36
∑M = 0 Az RBy .5 = 48.3 ∑M Ay =0 RBz .5 = 36.3
resolviendo : RAy = 19, 2 kN RBy = 28,8 kN RAz = 14, 4 kN RBz = 21, 6 kN
Los momentos de inercia de la sección serán:
1 1
Iz = .30 .40 3 = 160000 cm 4 Iy = .40.30 3 = 90000 cm 4
12 12
con lo cual:
E.I z = 2,1.104.103.160000.10−8 = 33600 kN .m 2
E.I y = 2,1.10 4.103.90000.10 −8 = 18900 kN .m 2

13. Diagramas de esfuerzos:
28,8 kN
19,2 kN 48 kN
z
14,4 kN
21,6 kN
A C B
36 kN
3m 2m
0− x−3
y M z = 19, 2. x
x = 0 → Mz = 0 x = 3 → M z = 57, 6
x M y = −14, 4.x
+ x = 0→ My =0 x = 3 → M y = −43, 2
Mz
3− x −5
57,6
M z = 28,8.(5 − x )
43,2
x = 3 → M z = 57, 6 x = 5 → Mz = 0
- M y = −21, 6.(5 − x )
x x = 3 → M y = −43, 2 x =5→ My =0
My
Por el método de la ecuación diferencial de la elástica:
Flechas en plano xy:
0− x−3 M z = 19, 2.x 3− x −5 M z = 28,8.(5 − x) = 144 − 28,8.x
2 2
d y d y
E .I z . = − M z = −19, 2.x E .I z . = − M z = 28,8.x − 144
dx 2 dx 2
dy x2 dy x2
E.I z . = −19, 2. + C1 E.I z . = 28,8. − 144.x + C3
dx 2 dx 2
3 3
x x x2
E.I z . y = −19, 2. + C1 .x + C2 E.I z . y = 28,8. − 144. + C3 .x + C4
6 6 2
condiciones de contorno :
dy  dy 
x = 0 → y0 − 3 = 0 x = 5 → y3−5 = 0 x = 3 → y0 −3 = y3−5 x =3→  = 
dx 0 −3 dx 3−5
operando : C1 = 67, 2 C2 = 0 C3 = 283, 2 C4 = −216
x3
−19, 2. + 67, 2.x
0− x−3 y= 6 → yC = y ( x = 3) = 0.0034 m = 0, 34 cm ↓
33600

14. Flechas en plano xz:
0− x−3 M y = −14, 4.x 3− x −5 M y = −21, 6.(5 − x) = −108 + 21, 6.x
d 2z d 2z
E .I y . = − M y = 14, 4.x E .I y . = − M y = −21, 6.x + 108
dx 2 dx 2
dz x2 dz x2
E.I y . = 14, 4. + C1 E.I y . = −21, 6. + 108.x + C3
dx 2 dx 2
3 3
x x x2
E.I y .z = 14, 4. + C1.x + C2 E.I y .z = −21, 6. + 108. + C3 .x + C4
6 6 2
condiciones de contorno :
dz  dz 
x = 0 → z0 − 3 = 0 x = 5 → z3 − 5 = 0 x = 3 → z 0 − 3 = z3− 5 x =3→  = 
dx 0−3 dx 3−5
operando : C1 = −50, 4 C2 = 0 C3 = −212, 4 C4 = 162
x3
14, 4. − 50, 4.x
0− x −3 z= 6 → zC = z ( x = 3) = 0.0046 m = 0, 46 cm ↓
18900
Calculemos zC, por el método de los Teoremas de Mohr:
14,4 kN z
36 kN 21,6 kN
A C
B
4800 Kg
x
zC
z(x)
y
Si abatimos el plano horizontal xz hacia el vertical xy la figura quedará:
tag. en A
δBA
C δCA
14,4 kN hC
21,6 kN
θyA zC
A C
B
4800 Kg
x
y
36 kN
z(x)
z

15. 0− x−3 M y = − 14, 4. x 3− x−5 M y = − 21, 6.(5 − x )
B 3 5
M
Q B AB ∫ M y .dx.(5 − x ) ∫ ( −14, 4.x ).dx.(5 − x ) + ∫ [ −21, 6.(5 − x ) ].dx.(5 − x )
δ BA = = A
= 0 3
E .I y E .I y 18900
δ BA = − 0, 01333 ( punto B por debajo tan gente en A )
δ BA 0, 01333
tagϑ yA ≅ θ yA = = = 0, 00267 rad → ϑ yA = − 0, 00267 rad
5 5
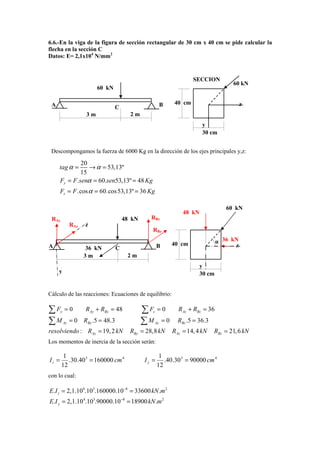
zC = hC − δ CA (ver figura)
hC = tagθ yA .3 ≅ ϑ yA .3 = 0, 00267.3 = 0, 00801 m
C 3
Q M AC ∫ M y .dx.(3 − x) ∫ (−14, 4.x).dx.(3 − x)
δ CA = C = A
= 0
= −0, 00343 m
E.I y E .I y 18900
(el punto C está por debajo de la tan gente en A)
zC = hC − δ CA = 0, 00801 − 0, 00343 = 0, 00458 m → zC = −0, 46 cm
δC = ( yC ) + ( zC ) = ( 0,34 ) + ( −0, 46 ) = 0, 57 cm
2 2 2 2
zC 0, 46
tag β = = → β = 53, 5º
yC 0, 34
48 kN
z 36 kN
A C
B
4800 Kg
zC yC
β
y(x)
z(x) δC
y
C´