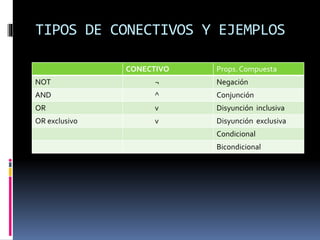
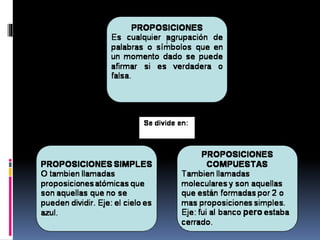
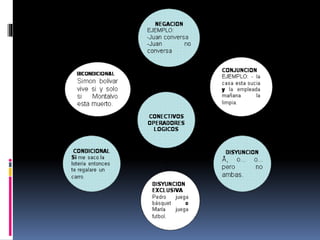
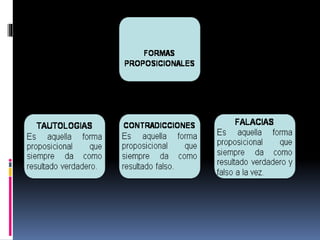
El documento define una proposición como un juicio mental que afirma o niega la relación entre un sujeto y un predicado. Las proposiciones se clasifican en simples o compuestas. Las proposiciones simples no contienen negaciones u operadores lógicos entre oraciones, mientras que las compuestas sí. Las formas proposicionales pueden ser tautologías, contradicciones o falacias/indeterminadas.

1. PROPOSICIONES

2. TEMAS A EXPONER
 DEFINICION GENERAL DE PROPOSICION
 CLASIFICACION
 CLASES DE PROPOSICIONES
 FORMAS PROPOSICIONALES

3. DEFINICIÓN GENERAL
En filosofía se entiende por proposición el acto mental por el cual se
expresa un juicio en el que se afirma o niega la correspondencia entre un
sujeto y un predicado dados. La proposición se expresa mediante una
oración o frase, pero no debe confundirse con ella, ya que la
proposición se refiere al juicio que se emite, y no a la expresión gramatical
que se utiliza para expresarlo. Así, las frases "hoy es martes" y "hoy es el
día siguiente al lunes", expresan el mismo juicio, aunque con dos frases u
oraciones gramaticales diferentes.

4. CLASIFICACIÓN
 PROPOSICIONES SIMPLES
 PROPOSICIONES COMPUESTAS

5. PROPOSICIONES SIMPLES
 Son aquellas que no tienen oraciones
componentes afectadas por negaciones
("no") o términos de enlace como
conjunciones ("y"), disyunciones ("o") o
implicaciones ("si . . . entonces"). pueden
aparecer términos de enlace en el sujeto o
en el predicado, pero no entre oraciones.

6. PROPOSICIONES COMPUESTAS
 Una proposición será compuesta si no es
simple. Es decir, si está afectada por
negaciones o términos de enlace entre
oraciones componentes.

7. CONECTIVOS (OPERADORES) LÓGICOS
 Son aquellos que sirven para
formar proposiciones más
complejas (compuestas o
moleculares).

8. TIPOS DE CONECTIVOS Y EJEMPLOS
CONECTIVO Props.Compuesta
NOT ¬ Negación
AND ^ Conjunción
OR v Disyunción inclusiva
OR exclusivo v Disyunción exclusiva
Condicional
Bicondicional

9. Ejemplos
 Sen(x) no es un número mayor que 1. (Compuesta)
 El 14 y el 7 son factores del 42. (Simple)
 El 14 es factor del 42 y el 7 también es factor del 42. (Compuesta)
 El 2 o el 3 son divisores de 48. (Simple)
 El 2 es divisor de 48 o el 3 es divisor de 48. (Compuesta)
 Si x es número primo, entonces x impar. (Compuesta)
 Si x > 10, entonces 2x - 3 > 16. (Compuesta)
 No todos los números primos son impares. (Compuesta)

10. FORMAS PROPOSICIONALES
Existen tres formas proposicionales:
 TAUTOLOGIAS: es aquella forma proposicional
que da como resultado verdadero.
 CONTRADICCIONES: es aquella forma
proposicional que siempre da como resultado
falso.
 FALACIAS O INDETERMINADA: es aquella forma
proposicional que siempre es verdadera y falsa a la
vez.

11. MAPAS
CONCEPTUALES