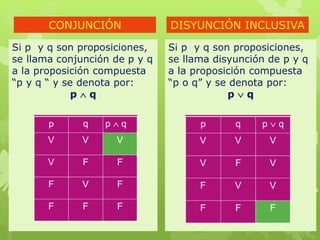
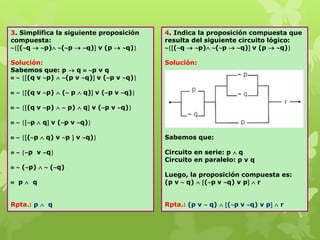
Este documento resume la lógica proposicional, incluyendo proposiciones, conectores lógicos como conjunción, disyunción, condicional y bicondicional, tablas de verdad y circuitos lógicos. Explica que la lógica proposicional estudia las relaciones entre proposiciones mediante conectores lógicos y trata de determinar la verdad o falsedad de proposiciones.

1. LÓGICA PROPOSICIONAL

2. • Es una parte de la
lógica matemática,
llamada también
«lógica de las
proposiciones sin
analizar».
• Estudia las relaciones
entre las
proposiciones
mediante la conexión
lógica de estas.
• Trata de la verdad o
falsedad de una o
varias proposiciones.
LÓGICA PROPOSICIONAL PROPOSICIÓN
• Es todo enunciado al que
se le puede asignar un
valor de verdad.
Clases de proposiciones:
• Proposición simple: es
aquella que no está
relacionada con otras
proposiciones.
• Proposición compuesta:
es aquella que se forma por
dos o más proposiciones
unidas por los conectores
lógicos.

3. CONECTORES LÓGICOS
Son símbolos que unen dos o más proposiciones
simples para formar una proposición compuesta.
Los conectores lógicos son:

4. CONJUNCIÓN
Si p y q son proposiciones,
se llama conjunción de p y q
a la proposición compuesta
“p y q “ y se denota por:
p  q
DISYUNCIÓN INCLUSIVA
Si p y q son proposiciones,
se llama disyunción de p y q
a la proposición compuesta
“p o q” y se denota por:
p  q

5. DISYUNCIÓN EXCLUSIVA
Si p y q son proposiciones,
se llama disyunción exclusiva
de p y q a la proposición
compuesta “o p o q” y se
denota por:
p Δ q
p q p Δ q
V V F
V F V
F V V
F F F
CONDICIONAL
Si p y q son proposiciones,
se llama condicional de p y q
a la proposición compuesta
“si p, entonces q” y se
denota por:
p  q
p q p → q
V V V
V F F
F V V
F F V

6. BICONDICIONAL
Si p y q son proposiciones,
se llama bicondicional de p y
q a la proposición compuesta
“ p, si y solo sí q” y se
denota por:
p ↔ q
p q p ↔ q
V V V
V F F
F V F
F F V
NEGACIÓN
Si p es una proposición,
entonces “no p” es la
negación de p y se denota
por:
~ p

7. LEYES DE LA LOGICA PROPOSICIONAL

8. CIRCUITOS LÓGICOS
Los circuitos lógicos se utilizan para adoptar decisiones
específicas de «verdadero - falso» sobre la base de la
presencia de múltiples señales de «verdadero-falso» en
las entradas.

9. EJERCICIOS
1. Si la proposición (p   q)   r es
falsa, determina el valor de verdad de
las siguientes proposiciones:
I.  p v (r  q)
II. ( q  p)   q
III. (q   r)  ( r  p)
Solución:
Partimos de:
(p   q)   r  F
V F
p   q  V  r  F
p  V ; q  F r  V
Luego:
I. F v (V  F)  F v F  F
II. (V  V)  V  V  V  V
III. (F  F)  (F  V)  F  F  F
Rpta.: FVF
2. Elabora la tabla de verdad de la
siguiente proposición compuesta:
( p  q)  ( q  p)
Luego, indica si es una tautología,
contradicción o contingencia.
Solución:
2 proposiciones: p y q
Es una contingencia.
Rpta.: Contingencia
p q (p  q)  (q  p)
V V F V V F F F V
V F F V F V V V V
F V V V V F F F F
F F V F F V V F F

10. 3. Simplifica la siguiente proposición
compuesta:
(q  p) (p  q) v (p  q)
Solución:
Sabemos que: p  q  p v q
  (q v p)  (p v q) v (p v q)
  (q v p)  ( p  q) v (p v q)
  (q v p)   p)  q v (p v q)
  p  q v (p v q)
  (p  q) v p  v q)
  p v q
  (p)   (q)
 p  q
Rpta.: p  q
4. Indica la proposición compuesta que
resulta del siguiente circuito lógico:
(q  p) (p  q) v (p  q)
Solución:
Sabemos que:
Circuito en serie: p  q
Circuito en paralelo: p v q
Luego, la proposición compuesta es:
(p v  q)  (p v q) v p  r
Rpta.: (p v  q)  (p v q) v p  r