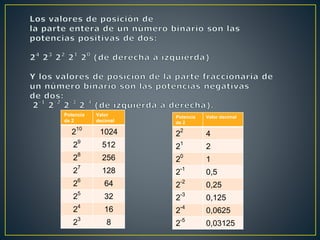
El documento explica los sistemas numéricos más comunes como el decimal, binario, hexadecimal y octal. El sistema decimal tiene base 10 y utiliza los símbolos 0-9, mientras que el binario tiene base 2 y usa solo 0s y 1s debido a que las computadoras operan internamente en binario. También describe cómo convertir entre diferentes sistemas numéricos.

2. Los sistemas numéricos forman la base
de todas las transformaciones de información
que suceden dentro del ordenador , es por
ello que el conocimiento de los sistemas
numéricos es importante en el estudio de las
computadoras y del procesamiento de datos.

3. Cada uno de los símbolos tiene
un valor fijo superior en uno al
valor del símbolo que lo
precede en la progresión
ascendente: 0,1,2,3,4,5,6,7,8,9.
 Cuando se combinan varios
símbolos (o dígitos), el valor
del número depende de la
"posición relativa" de cada uno
de los dígitos y del "valor de los
dígitos", el primero es el "valor
posicional" y el segundo es el
"valor absoluto".

5. El incremento de valor de cada
posición de dígito depende de la base o
raíz del sistema numérico. De este
modo, en el sistema decimal, que
utiliza la base 10, el valor de las
posiciones de dígito a la izquierda del
dígito menos significativo (o posición de
unidades), aumenta en una potencia de
10 por cada posición.

6. El sistema decimal tiene base (raíz) 10,
porque dispone de 10 símbolos (0-9)
numéricos discretos para contar. Entonces, la
"base" de un sistema numérico es la cantidad
de símbolos que lo componen y el valor que
define al sistema.

7. Ejemplo
de valor relativo de los dígitos
Veamos el número decimal 9545.
El valor relativo de cada dígito es aún
más claro si el número se expresa en
potencias de diez.
Cualquier entero positivo n que se
representa en el sistema decimal como
una cadena de dígitos decimales,
puede expresarse también como una
suma de potencias de diez ponderada
por un dígito.
9000+500+40+5=9.545

8. Esto es notación expandida para el entero.
Las potencias de diez: 100 = 1; 101 = 10; 102 =
100; 103 = 1000
corresponden respectivamente a los dígitos en un
entero decimal cuando se leen de derecha a
izquierda.
Cualquier valor fraccionario m, representado en el
sistema decimal por una cadena de dígitos
decimales junto con un punto decimal intercalado,
puede expresarse también en notación expandida
usando potencias negativas de 10.
9.545 = 9 x 10
3
+ 5 x 10
2
+ 4 x 10
1
+ 5 x 10
0
= 9 x 1000 + 5 x 100 + 4 x 10 + 5
x 1

9. El valor posicional de los dígitos a la
derecha del punto decimal es,
respectivamente:
10
-1
=
1
/
10
10
-2
=
1
/
100
10
-3
=
1
/
1000

12. La computadora utiliza el sistema binario para su
funcionamiento interno, este sistema está
compuesto por los símbolos 1 y 0. Los
componentes físicos del ordenador solo
representan dos estados de condición: Apagado
/prendido, abierto /cerrado, magnetizado/ no
magnetizado es por ello que esta opera en binario.
Se representan en base dos.

13. Potencia
de 2
Valor
decimal
210
1024
29
512
2
8
256
2
7
128
2
6
64
25
32
24
16
2
3
8
Potencia
de 2
Valor decimal
2
2
4
21
2
20
1
2
-1
0,5
2
-2
0,25
2
-3
0,125
2-4
0,0625
2
-5
0,03125

14. 10101(2)=1X2
4
+0X2
3
+1X2
2
+0x21+1X2
0
=16+0+4+0+1=21(10)
(10101)2=(21)10
11001101(2)=1X2
7
+1X2
6
+0X2
5
+0X2
4
+1X2
3
+1X2
2
+0X2
1
+1X2
0
=128+64+0+0+8+4+0
+1=205(10)
(11001101)2=(205)10

15. Se utiliza a diario.
Está compuesto por los
símbolos 0 al 9.
Tiene base (raíz) 10.
Utiliza diez símbolos:
0,1,2,3,4,5,6,7,8,9, (cifras
decimales)

16. 7.824(10)= 7x103
+8x102
+2x101
+4x100
=7000+800+20+4
4.382(10)=4x103
+3x102
+8x101
+2x100
=4000+300+80+2

17. Este sistema comprime los números binarios para
hacerlos más sencillos de tratar este sistema
posee 16 símbolos.
El sistema numérico hexadecimal de (base 16)
surge como un medio para representar los
números binarios de gran magnitud. Cada digito
hexadecimal representa cuatro dígitos binarios. La
lista completa de símbolos hexadecimales consta,
por lo tanto, del 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C,
D, E y F, en orden ascendente de valor.

18. 8DB
8X162+11X161+13X160
8X256+11X16+13X1
2048+176+13=2237
4AC
4X162
+10X161
+12X160
4X256+10X16+12X1
1024+160+12=1196

19. El sistema de numeración octal es un
sistema de numeración en base 8, una
base que es potencia exacta de 2 o de la
numeración binaria.
El sistema octal usa 8 dígitos (0, 1, 2, 3,
4, 5, 6, 7) y tienen el mismo valor que en
el sistema de numeración decimal.

20. 700(8)
700=7x82
+0x81
+0x80
448+0+0= 448
542(8)
542=5x8
2
+4x8
1
+2x8
0
320 +32+2=354

21. Decimal a binario: Para cambiar de base
decimal a cualquier otra base se divide el
número que se quiere convertir por la
base del sistema al que se quiere cambiar,
los resultados que se obtengan en el cociente
deben seguir dividiéndose hasta que este
resultado sea menor que la base. Los
residuos que resulten de todas las divisiones
en orden progresivo se irán apuntando de
derecha a izquierda.

22. 49:2=24 Resto =1
24:2=12 « =0
12:2=6 « =0
6:2=3 « =0
3:2=1 « =1
(1 1 0 0 0 1)2

23. El mecanismo de conversión es el
mismo que el descripto en la conversión
de decimal a binario , pero dividiendo el
número por 16, que es la base del
sistema hexadecimal.

24. 6898(10)
6898:16=431.125 Resto =2
431:16=26.9375 « =F
26:16=1.625 « =A
1:1=1
1 A F 2 (16)

25. Dividimos entre ocho
1598(10)
1598:8 = 199.75 Resto = 6
199:8 = 24.875 « = 7
24:8 =3 « = 0
3:3 =3
3 0 7 6 (8)

26. Binario a hexadecimal: se divide el
número binario en grupos de cuatro
dígitos binarios, comenzando desde
la derecha y se reemplaza cada grupo
por el correspondiente símbolo
hexadecimal. Si el grupo de la
extrema izquierda no tiene cuatro
dígitos, se deben agregar ceros hasta
completar 4 dígitos.

28. 11111111=1 Byte = 8 bits
11111111(2)=
1x27+1x26+1x25+1x24+1x23+1x22+1x21
+1x20=128+64+32+16+8+4+2+1=255(10)