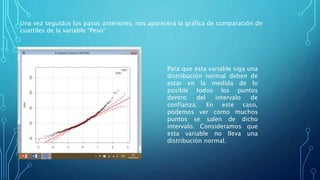
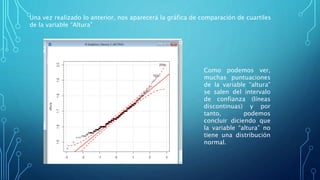
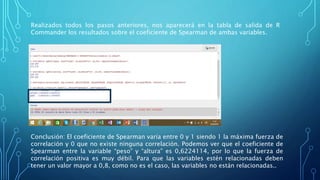
Este documento describe los pasos para analizar la relación entre las variables "Peso" y "Altura" en un conjunto de datos. Primero, se comprueba la normalidad de ambas variables utilizando gráficas de cuartiles, lo que muestra que ninguna sigue una distribución normal. Luego, se grafican los datos para ver la relación, mostrando poca correlación. Finalmente, se calcula el coeficiente de Spearman, dando como resultado 0.6224, indicando una correlación débil entre las variables.

1. R COMMANDER: RELACIÓN
ENTRE LAS VARIABLES

2. 1. Relación y fuerza de
relación entre las
variables

3. 1. Lo primero que debemos hacer es especificar el directorio de trabajo una vez
que hayamos abierto R Commander.
Pulsamos en “Fichero” y seguidamente
“Cambiar directorio de trabajo”. La
carpeta que yo he seleccionado es
“SEMINARIO 8 ESTADÍSTICA”

4. 2. Una vez que hemos seleccionado el directorio de trabajo, cargamos el archivo con el
conjunto de variables. Pulsamos sobre “Datos” y posteriormente sobre “Cargar conjunto de
datos”
Nos aparece este cuadro
con el archivo
“activossalud.Rdata”.

5. 3. Tenemos que observar si las variables “Peso” y “Altura” presentan algún tipo de relación
entre ellas. Utilizaremos, por tanto, el test paramétrico o el no paramétrico dependiendo
de si hay normalidad o no en las variables, cosa que tenemos que comprobar.
 Vamos a comprobar primeramente la normalidad de la variable “Peso”. Pulsamos pues
en “Gráficas” y luego sobre “gráficas de comparación de cuartiles”
Pulsamos en la variable “Peso” y en la ventana de
“Opciones” elegimos “Distribución normal”

6. Una vez seguidos los pasos anteriores, nos aparecerá la gráfica de comparación de
cuartiles de la variable “Peso”
Para que esta variable siga una
distribución normal deben de
estar en la medida de lo
posible todos los puntos
dentro del intervalo de
confianza. En este caso,
podemos ver como muchos
puntos se salen de dicho
intervalo. Consideramos que
esta variable no lleva una
distribución normal.

7.  Ahora vamos a comprobar la normalidad de la variable “Altura”. Seguiremos los
mismos passo que antes pero eligiendo en este caso la variable “altura”. Pulsamos en
“Gráficas” y luego sobre “gráfica de comparación de cuartiles”

8. Una vez realizado lo anterior, nos aparecerá la gráfica de comparación de cuartiles
de la variable “Altura”
Como podemos ver,
muchas puntuaciones
de la variable “altura”
se salen del intervalo
de confianza (líneas
discontinuas) y por
tanto, podemos
concluir diciendo que
la variable “altura” no
tiene una distribución
normal.

9. Como ninguna de las variables presenta una distribución normal, debemos usar un test
no paramétricos en nuestro caso el Rho de Spearman.
4. Una vez conocida la prueba a utilizar debemos estudiar el tipo de relación entre las
variables y la fuerza de relación.
 TIPO DE RELACIÓN (REGRESIÓN) hay entre ellas  pulsamos sobre “Gráficas” y
luego sobre “Diagramas de dispersión”

10. Realizado todo lo anterior, obtendremos la gráfica de relación entre las variables “peso” y
“altura”
Al principio de la gráfica
podemos ver una cierta
relación entre las variables
(los puntos se acercan a la
“línea de los mínimos
cuadrados”, pero a medida
que aumentan los valores
no existe relación entre el
peso y la altura ya que las
puntuaciones están muy
alejadas de la línea de los
mínimos cuadrados.
Por tanto, NO EXISTE
relación entre las
variables.

11.  COMO DE FUERTE ES DICHA RELACIÓN en caso de que la hubiera (CORRELACIÓN)
Primero, pulsamos sobre
“Estadísticos”, luego “resúmenes” y
finalmente sobre “Matriz de
correlaciones”
Una vez realizado todo lo
anterior, nos aparece una
ventana en la cual
elegiremos ambas
variables. Además,
debemos elegir el
“coeficiente de
Spearman” porque son
dos variables
cuantitativas cuya
distribución no sigue la
normalidad.

12. Realizados todos los pasos anteriores, nos aparecerá en la tabla de salida de R
Commander los resultados sobre el coeficiente de Spearman de ambas variables.
Conclusión: El coeficiente de Spearman varía entre 0 y 1 siendo 1 la máxima fuerza de
correlación y 0 que no existe ninguna correlación. Podemos ver que el coeficiente de
Spearman entre la variable “peso” y “altura” es 0,6224114, por lo que la fuerza de
correlación positiva es muy débil. Para que las variables estén relacionadas deben
tener un valor mayor a 0,8, como no es el caso, las variables no están relacionadas..