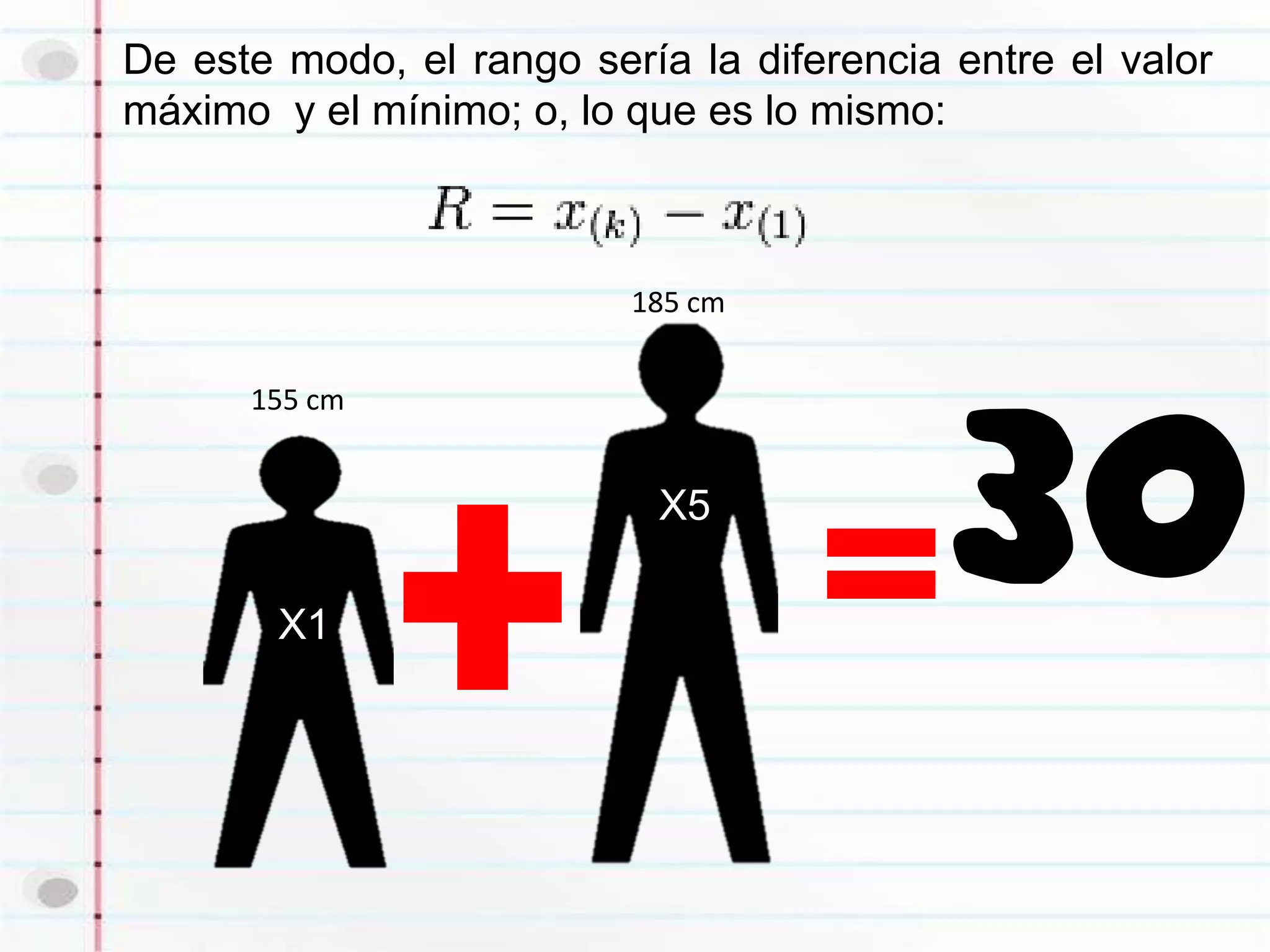
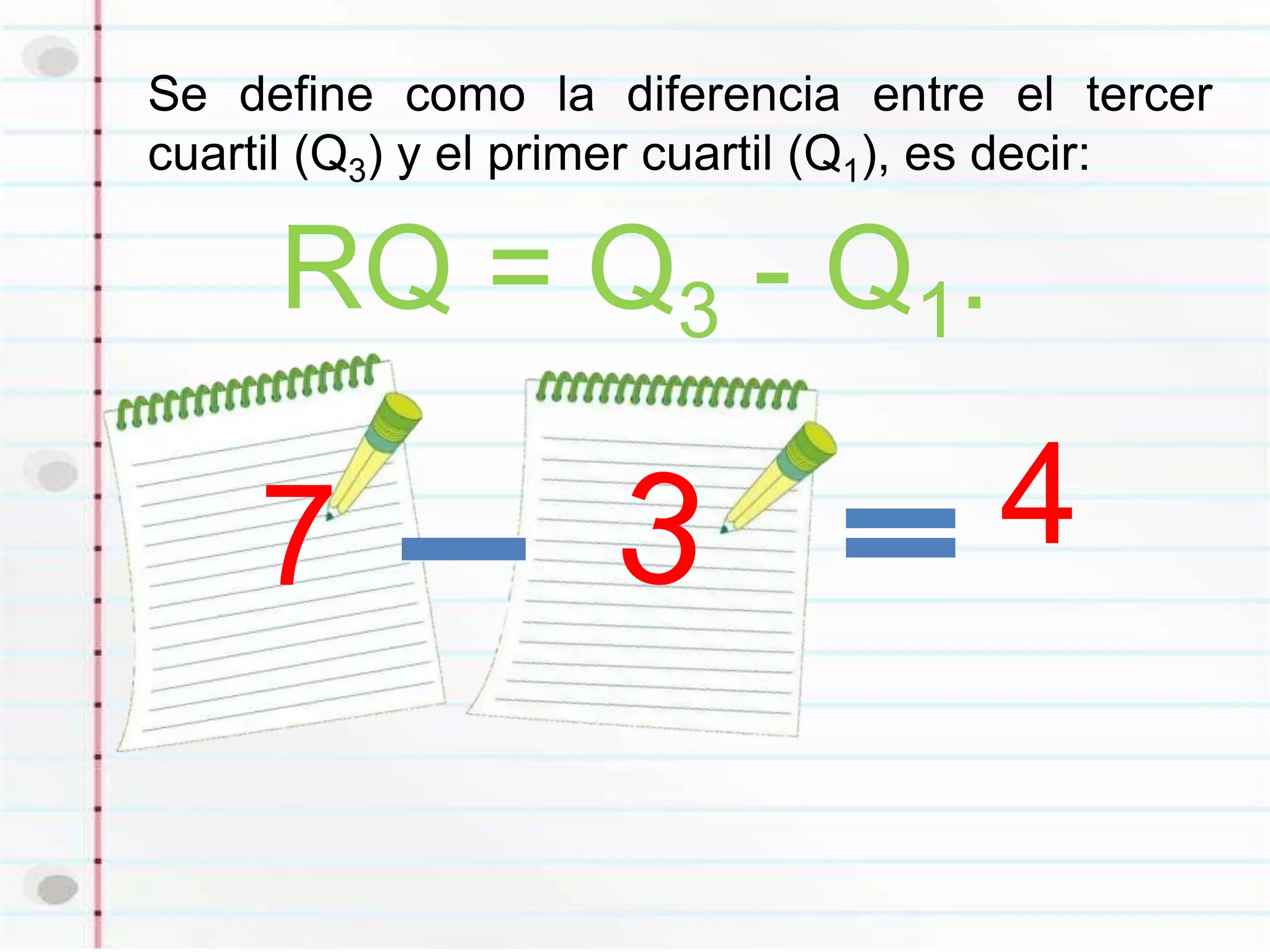
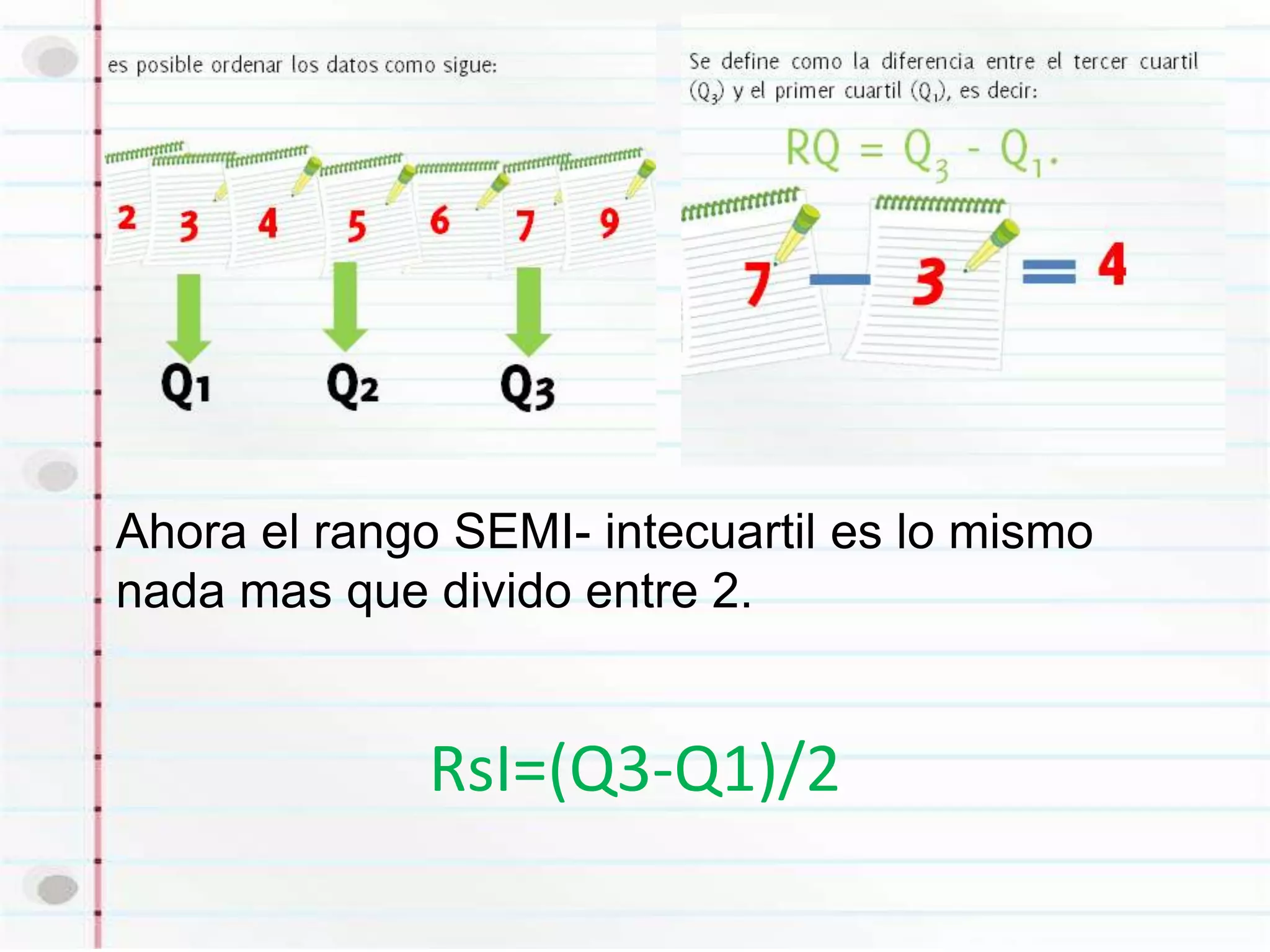
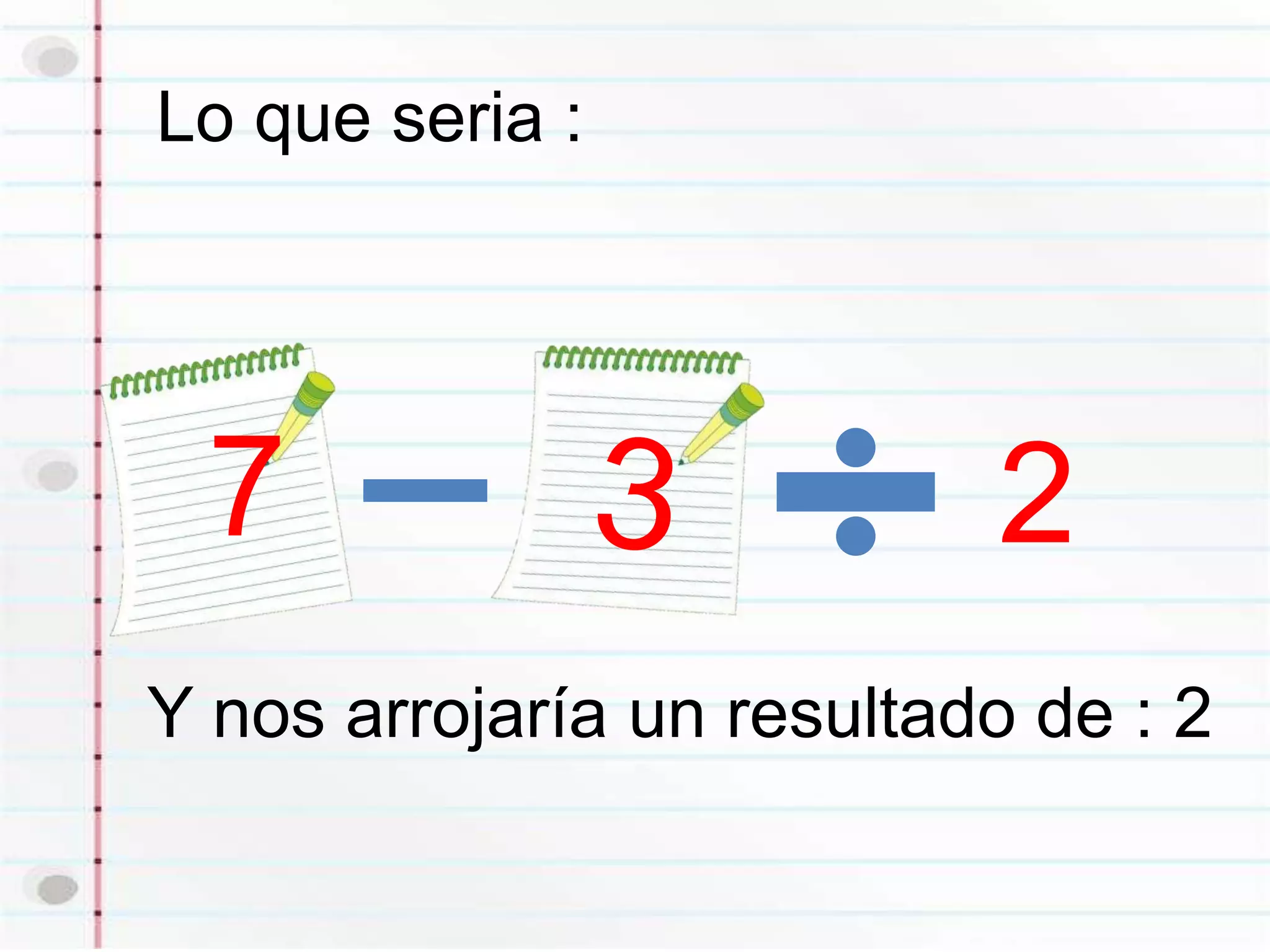
El rango es la diferencia entre el valor máximo y mínimo de un conjunto de datos y mide la dispersión de los datos. El rango intercuartil es la diferencia entre el tercer y primer cuartil y también mide la dispersión, ignorando valores extremos. El rango semi-intercuartil divide la diferencia entre el tercer y primer cuartil entre 2.

4. Es igual a la diferencia entre el valor máximo
y el valor mínimo.
Permite obtener una idea de la dispersión de
los datos, cuanto mayor es el rango, más
dispersos están los datos de un conjunto.

5. Por ejemplo, para una serie de datos de carácter
cuantitativo, como lo es la estatura medida en
centímetros, tendríamos :
185 cm
170 cm 182 cm
165 cm 155 cm

6. es posible ordenar los datos como sigue:
185 cm
170 cm 182 cm
155 cm 165 cm
X5
X4
X2 X3
X1

7. De este modo, el rango sería la diferencia entre el valor
máximo y el mínimo; o, lo que es lo mismo:
185 cm
30
155 cm
X5
X1

8. O rango intercuartil, a la diferencia entre el
tercer y el primer cuartil de una distribución. Es
una medida de la dispersión estadística.

9. Por ejemplo, para una serie de datos de carácter
cuantitativo, como lo son las calificaciones de los
alumnos:
5 3 6
2
7 4 9

10. es posible ordenar los datos como sigue:
2 3 4 5 6 7 9
Q1 Q2 Q3

11. Se define como la diferencia entre el tercer
cuartil (Q3) y el primer cuartil (Q1), es decir:
RQ = Q3 - Q1.
7 4

12. es un medio de la diferencia entre el primer y tercer
cuartiles. Es la mitad de la distancia requerida para
cubrir la mitad de las cuentas

13. Ahora el rango SEMI- intecuartil es lo mismo
nada mas que divido entre 2.
RsI=(Q3-Q1)/2

14. Lo que seria :
7 2
Y nos arrojaría un resultado de : 2