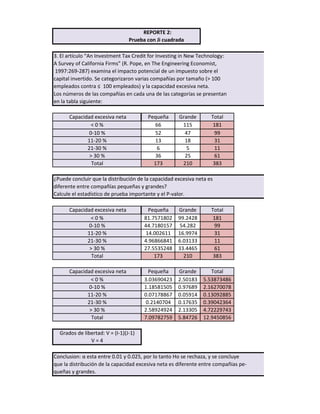
El documento presenta los resultados de una prueba Ji cuadrada que examina si la distribución de la capacidad excesiva neta es diferente entre compañías pequeñas y grandes. Los resultados muestran que el estadístico de prueba es significativo con un nivel de significancia entre 0.01 y 0.025, lo que lleva a rechazar la hipótesis nula de que la distribución es la misma entre tamaños de compañía. Por lo tanto, se concluye que la distribución de la capacidad excesiva neta difiere entre compañ

1. REPORTE 2:
Prueba con Ji cuadrada
3. El artículo “An Investment Tax Credit for Investing in New Technology:
A Survey of California Firms” (R. Pope, en The Engineering Economist,
1997:269-287) examina el impacto potencial de un impuesto sobre el
capital invertido. Se categorizaron varias compañías por tamaño (> 100
empleados contra ≤ 100 empleados) y la capacidad excesiva neta.
Los números de las compañías en cada una de las categorías se presentan
en la tabla siguiente:
Capacidad excesiva neta Pequeña Grande Total
< 0 % 66 115 181
0-10 % 52 47 99
11-20 % 13 18 31
21-30 % 6 5 11
> 30 % 36 25 61
Total 173 210 383
¿Puede concluir que la distribución de la capacidad excesiva neta es
diferente entre compañías pequeñas y grandes?
Calcule el estadístico de prueba importante y el P-valor.
Capacidad excesiva neta Pequeña Grande Total Formula para valore
< 0 % 81.7571802 99.2428 181
0-10 % 44.7180157 54.282 99
11-20 % 14.002611 16.9974 31
21-30 % 4.96866841 6.03133 11
> 30 % 27.5535248 33.4465 61
Total 173 210 383
Capacidad excesiva neta Pequeña Grande Total Formula para Ji cuad
< 0 % 3.03690423 2.50183 5.53873486
0-10 % 1.18581505 0.97689 2.16270078
11-20 % 0.07178867 0.05914 0.13092885
21-30 % 0.2140704 0.17635 0.39042364
> 30 % 2.58924924 2.13305 4.72229743
Total 7.09782759 5.84726 12.9450856
Grados de libertad: V = (I-1)(J-1)
V = 4
Conclusion: α esta entre 0.01 y 0.025, por lo tanto Ho se rechaza, y se concluye
que la distribución de la capacidad excesiva neta es diferente entre compañias pe-
queñas y grandes.

2. Ho:Que las diferencias en las diferentes categorias sean igual entre las compañias pequeñas y grandes.
Formula para valores esperados:
Eij = Oi.O.j/O..
Formula para Ji cuadrada:
X^2 = (Oij Eij)^2/Eij

3. eñas y grandes.